簇绒地毯织机提花装置的绕纱动态张力分析

夏胜华, 孙以泽, 孟 婥, 任国斌

(东华大学 机械工程学院， 上海 201620)



簇绒地毯织机提花装置的绕纱动态张力分析

夏胜华, 孙以泽, 孟 婥, 任国斌

(东华大学 机械工程学院， 上海 201620)

簇绒地毯织机纱线张力是影响提花质量的关键因素，为对其进行有效控制，研究了步进电动机输入对簇绒提花装置区间绕过纱线张力的动态变化情况。首先建立提花装置步进电动机的负载模型，并分析其角频率输入对输出电磁转矩的对应关系；然后，根据米纳科夫定理的原理，建立纱线段绕过提花罗拉前后纱线动态张力模型；进一步分析了步进电动机的输入与提花装置绕纱的输出动态张力之间的数学模型，在选定提花罗拉半径、中心距、纱线包角等初始条件下，利用迭代-欧拉法分析其数值变化情况，得出角频率输入与纱线张力输出之间的定量关系，并探究不同包角对纱线动态张力的影响机制，为不同绒高的簇绒地毯甚至满幅簇绒提花地毯的制造和研究提供参考。

簇绒地毯； 提花装置； 纱线张力； 步进电动机； 迭代-欧拉法

簇绒地毯以其优越的性能在纺织地毯产业的市场占有率不断增加，与其相对应的地毯簇绒装备的研究也越来越受到大家的重视。目前，满幅浮雕式提花地毯是国际上公认的较高品质的地毯，其绒高一般在2～16 mm[1]。地毯簇绒机的工作原理是电动机为提花装置提供动力，通过不同的控制方式使罗拉组具有不同的转速，形成不同的喂纱量，实现高低不同的绒高，从而使生产的毯面具有浮雕花型的图案效果[2]，因此，在地毯簇绒装备中，最关键的部分是对提花装置的设计与控制。

不同的提花装置具有不同的提花方式。常见的提花装置有：偏心提花装置、板条提花装置、罗拉提花装置、莫哈斯科(Mohasco)提花装置、斯克罗尔(Scroll)提花装置、视屏(video-tuft)提花装置等[3]。其中，斯克罗尔提花装置由于结构简单，运行可靠，变化喂纱罗拉可生产多层绒高等特点，在实际生产中应用非常广泛。

提花装置控制的实质是对纱线的喂给量或纱线动态张力的控制，纱线张力是影响加工质量、生产效率的重要参数。张力过大，纱线弹性拉长强力受损，增加断头；张力过小容易打滑，损失绒高真值[4]，因此，对纱线张力动态变化的研究具有重要的意义。国内许多学者也对此进行了相关的研究，徐洋等[1]研究了地毯簇绒系统纱线张力建模与分析，周廷泽等[5]研究了地毯簇绒装备的类齿轮特殊罗拉纱线牵引装置；高小平等[6]研究了提花装置到牵引罗拉之间的纱线动态张力分析。

本文基于斯克罗尔提花原理，分析提花装置区间绕纱的动态张力。在考虑实际工况的条件下，首先建立步进电动机的模型，探究其输出对提花装置绕纱张力变化的影响，然后运用米纳科夫定理相关知识建立提花装置的动态张力模型，进一步抽象出给定步进电动机输入对提花装置输出张力变化的数学模型，分析模型的特点并利用迭代-欧拉法的数学知识进行求解。综合分析结果可知，在输入不同的角频率条件下，可定量计算对应纱线输出的动态张力,并分析其变化规律，为不同绒高满幅花型地毯提供定值参考；随着中心距、提花轮半径、纱线绕过提花罗拉的角度等工艺参数的变化，探究了包角对纱线动态张力的影响机制，为簇绒地毯提花装置的设计和控制提供参考。

1 提花装置步进电动机负载模型

在提花过程中，不同的提花装置相对应的动力控制装置也不尽相同[7-8]。由于步进电动机结构简单，价格便宜，位置控制可靠等特点，是提花装置理想动力元件之一。步进电动机的工作原理是将电脉冲信号转变为角位移或线位移输出给机械装置。利用驱动器给定步进电动机的脉冲频率输入，使其控制提花轮具有不同的转速，从而改变纱线的送纱量，纱线的张力也发生变化。

本文是基于二相四线输入的步进电动机建立步进电动机负载模型，如图1所示。图中A、B为输入的脉冲序列，以控制步进电动机的机械输出，同时步进电机通过传动系统带动提花罗拉转动。

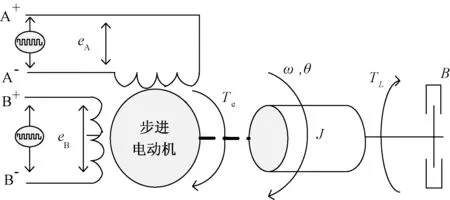
图1 步进电动机负载模型Fig.1 Load model of stepper motor

由电磁感应定律知A、B产生的反电动势为

(1)

(2)

由步进电动机的电压平衡方程，可得

(3)

(4)

由磁场对载流线圈的作用，可得

(5)

根据步进电动机转矩平衡方程，可得：

(6)

(7)

式中：eA、eB为A、B二相线圈反电动势；iA、iB为A、B二相线圈电流；VA、VB为A、B两相线圈输入电压；Km为步进电动机反电动势系数；Kt为步进电动机电磁转矩系数；Te为步进电动机励磁转矩；Td为步进电动机定位转矩；TL为负载转矩；Nr为转子齿数；Rm为步进电动机磁化绕组；R为线圈绕组电阻；L为线圈绕组电感；B为等效旋转阻尼；J为等效转动惯量；θ为转子转角；ω为转子转速。

根据以上步进电动机负载模型，如果给定输入脉冲频率的函数，可以计算出对应的机械输出角速度、电动机的输出转矩；进而由转矩平衡可以计算出负载转矩。其中，负载转矩的大小与提花装置绕纱张力的改变紧密相关。

2 提花装置绕纱的动态张力模型

采用步进电动机控制提花装置，其对应的提花装置结构和安装方式如图2所示。由步进电动机的输出轴与提花罗拉I的轴同步连接，提花罗拉I与II之间通过模数和齿数相同的2个齿轮同步连接，步进电动机带动提花罗拉I和II同步转动；纱线通过提花罗拉I的一侧进入，绕过2个罗拉后，从提花罗拉II的另一侧输出。

图2 提花装置结构和安装方式Fig.2 Structure and installation of jacquard device

在提花罗拉表面粘上一层磨砂纸，增大提花罗拉与纱线之间的摩擦力，从而达到纱线与提花罗拉的速度同步的目的。运用经典的欧拉(Euler)公式，可以计算纱线在静态条件下绕圆柱体前后纱线张力的变化关系，但是簇绒地毯织机在实际工作的过程中，提花罗拉附近的纱线处在动态的变化之中，为使其结果更具有真实性和准确性，需要将其实际工况纳入考虑，因此，需要对欧拉公式进行改进应用，米纳科夫在1941年对此进行了研究，分析了纱线在动态条件下绕过柱体表面的张力变化机制，拓展了欧拉公式的应用条件。

2.1 米纳科夫定理的应用

米纳科夫定理的理论虽然分析了纱线绕过柱体表面的动态张力变化情况，但由于其采用的是自然坐标，在实际运用中不便[9]。本文将利用米纳科夫定理的原理，在直角坐标系中，分析在非欧拉条件下纱线绕过提花装置单个提花罗拉的动态变化情况。纱线绕过单个罗拉的张力如图3所示。纱线从点S0(x0，y0)接触并绕过转速为ω的圆柱体一段圆弧到S1(x1，y1)处离开，任意选取圆弧S0S1上的一微小段dS为研究对象，进行受力分析。

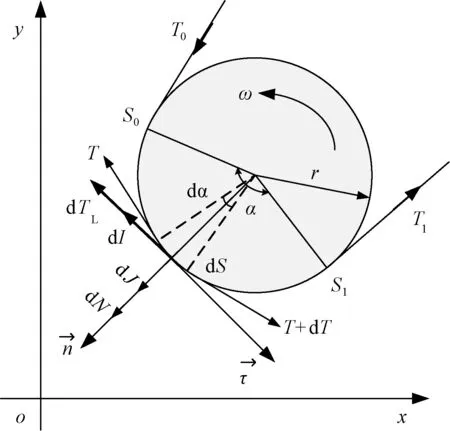
图3 纱线绕单个罗拉的张力分析Fig.3 Tension analysis of yarn around single roller

设dS段纱线对应包角为dα，纱线速度v=ωr，引入侧的张力为T，经圆弧段后引出侧张力为T+dT；法向反力为dN。

纱线摩擦力 dF=μdN

(8)

切向惯性力dI=admS=amrdα

(9)

(10)

式中：μ为纱线与接触面的摩擦因数；m为单位纱线的质量；ms为纱线微弧段dS的质量；a为纱线运动加速度。

(11)

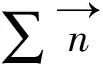
(12)

假设纱线此时速度v=const(常数)，即a=0；令微小段纱线dS的高阶无穷小为零，根据无穷小的相关理论有：

由式(8)～(10)对式(11)、(12)化简得：

(13)

dT-dF=0

(14)

(15)

对式(15)进行微分方程求解，可得：

(16)

将式(16)代入式(14)，解微分方程可得：

(17)

簇绒地毯织机提花装置中的提花罗拉通常采用成对的圆柱型的提花罗拉调节纱线张力，运用上述分析的单个提花罗拉的受力分析结果，可以很容易建立提花装置绕纱的动态张力模型。

2.2 动态张力模型的建立

在直角坐标系中，建立提花装置绕纱的动态张力分析，如图4所示。纱线以初始张力T0从提花罗拉Ⅰ一侧绕过后，纱线的张力为T1；又经过提花罗拉Ⅱ的张力控制，纱线的张力为T2。2个提花罗拉中心O1O2的连线与x轴平行，距离为l，引入侧纱线与x轴夹角为β1，引出侧纱线与x轴夹角为β2，纱线经过提花罗拉组的结合分离点依次为S1、S2、S3、S4。

图4 提花装置绕纱的动态张力分析Fig.4 Dynamic tension analysis of jacquard device winding yarn

根据几何知识得：

设α=α1+α2，则

(18)

对提花装置中一对提花罗拉分别运用上文中的米纳科夫定理的研究，即根据式(17)，对罗拉Ⅰ：

(19)

对罗拉Ⅱ：

(20)

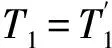
所以，根据式(18)～(20)，可得：

(21)

由提花罗拉的转矩平衡，可得

T2-T0=TL/r

(22)

由式(21)、(22)消去T0，可得

(23)

由式(23)可得到提花装置绕纱的动态张力模型，分析可知，在包角、摩擦因数、提花轮半径一定时，绕纱的张力主要与负载相关。

3 仿真分析

3.1 迭代-欧拉法解数学模型

根据提花装置步进电动机负载模型和绕纱动态张力模型，精简出对应的数学模型式(1)～(7)、(23)共8个方程，其中未知变量有9个，均为关于时间t的变量。由于数学模型中方程(1)、(2)进行拉斯变换无法求解，故利用数值分析中迭代的思想，以角频率ω(t)作为输入，T2作为输出，在给定时间内循环迭代；因过程中存在微分的算法，因而引进欧拉算法，即采用迭代-欧拉法[10]进行求解。

在进行数值计算前，需要确定相关方程对应的系数。步进电动机为日本MOONS′公司的二相23系列，型号为23HS0030；纱线采用BCF丙纶地毯纱；为简化计算，假设引入侧纱线张力与输出侧张力的方向均与提花轮的中心线O1O2垂直，实际情况可任取。通过查表、取值确定各系数的数值如表1所示。

表1 数值求解主要参数Tab.1 Main parameters of MatLab

3.2 MatLab仿真及分析

在确定数学模型中各方程的系数后，利用MatLab进行数值求解，其算法流程图如图5所示。

图5 模型算法流程图Fig.5 Flowchart of model algorithm

设给定的输入信号为ω(t)=3.14t;0≤t≤10，即0≤ω≤31.4;0≤n≤300；步长h取0. 1，步进电动机励磁转矩Te，提花装置绕纱的动态张力T2随角频率ω的变化情况如图6、7所示。

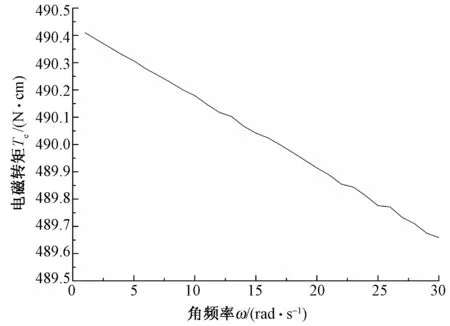
图6 步进电动机电磁转矩-角频率曲线Fig.6 Curve of stepper motor electromagnetic torque-angular frequency

图7 提花装置绕纱的张力-角频率曲线Fig.7 Curve of jacquard device winding yarn tension-angular frequency

由图6、7中的结果对比分析可知：在不同的ω下，可以定量计算出其对应的纱线张力，而且纱线的张力随着角频率的增大而减小，与步进电动机的励磁转矩具有相同的变化规律；同时，纱线的张力随着角频率的增大，对应纱线张力波动也越明显。

若取ω=10 rad/s不变，纱线绕过提花轮包角α在π～4π间变化，利用上述数学模型求解，绕纱动态张力随包角变化曲线如图8所示。

图8 提花装置绕纱的张力-包角曲线Fig.8 Curve of jacquard device winding yarn tension-wrap angle

由图8中的曲线分析可知：当提花罗拉角频率一定时，绕过提花装置绕纱的动态张力随着包角的增大而增大；当包角在π～2.5π区间时，绕纱的动态张力随包角增大而迅速增大；在2.5π～4π时区间，绕纱的动态张力趋于稳定，基本不变。

4 结 论

本文研究了步进电动机输入控制的提花装置绕纱的动态张力变化机制，并探究了包角对绕纱动态张力的影响规律，得到以下结论。

1)随角频率的不断增大，电磁转矩和绕纱的动态张力不断减小，波动增大，且二者具有相似的变化规律。

2)在不同的ω下，可以定量计算出其对应的纱线张力，为不同绒高的满幅簇绒地毯需要的纱线张力提供数值参考。

3)绕纱的动态张力会随着纱线包角增大而迅速增大，但包角增大到2.5π后，绕纱的动态张力会趋于稳定，作用不明显。

FZXB

[1] 徐洋，孙志军，孟婥，等.地毯簇绒系统纱线张力建模与分析[J]. 纺织学报，2010,31(12):116-121. XU Yang, SUN Zhijun, MENG Zhuo, et al. Modeling and analysis on yarn tension of carpet tufting machine[J].Journal of Textile Research,2010, 31(12):116-121.

[2] 陈广锋，吴春晖，孙以泽,等.三圈高地毯簇绒机提花控制系统[J].纺织学报，2008,29(3)：113-117. CHEN Guangfeng,WU Chunhui,SUN Yize, et al. Jacquard control system for three-level loop carpet tufting machine [J].Journal of Textile Research, 2008,29(3):113-117.

[3] 薛士鑫. 机织地毯[M]. 北京：化学工业出版社，2003：330-336. XUE Shixin. Machine-Made Carpet [M].Beijing: Chemical Industry Press,2003:330-336.

[4] 庾在海，吴文英. 纱线张力动态测试方法[J].自动化仪表,2005, 26(10):33-35. YU Zaihai, WU Wenying. Dynamic testing method for yarn tension[J]. Automation Instrumentation, 2005, 26(10):33-35.

[5] 周廷泽，孟婥，孙菁菁,等. 地毯簇绒装备的类齿轮特殊罗拉纱线牵引装置[J].东华大学学报:自然科学版，2007,33(2):171-174. ZHOU Tingze, MENG Zhuo, SUN Jingjing, et al.

Special gear-like roller device to pull yarn used in carpet tufting machine[J]. Journal of Donghua University: Natural Science Edition, 2007,33(2):171-174.

[6] 高小平，孙以泽，孟婥,等. 簇绒提花地毯纱线束动态张力分析[J]. 纺织学报，2012,33(2):40-45. GAO Xiaopin, SUN Yize, MENG Zhuo, et al. Dynamic tenson analysis of yarn strand in tufting jacquard carpets [J]. Journal of Textile Research, 2012, 33(2):40-45.

[7] ZHAO Yue，DAI Huiliang. Advanced tufted carpet pattern technology [J]. Journal of Zhejiang University: Science A, 2006(3):113-117.

[8] CHEN Guangfeng，YANG Yanzhu，ZOU Kun, et al. Electromagnetic clutch based high-low carpet jacquard control system[C]/ / IITA 2nd International Symposium on Intelligent Information Technology Application Workshop. Shanghai: IEEE Computer Society，2008:176-179.

[9] 吴震世. 论曲面上纱线的导向与纱线张力[J].纺织科学与研究,1997(1)：37-47. WU Zhenshi. Research of yarn guidance and yarn tension on curved surface [J]. Textile Science Research, 1997(1)：37-47.

[10] 姜健飞，吴笑千，胡良剑. 数值分析及其MatLab实验[M].北京：清华大学出版社, 2004：20-30. JIANG Jianfei, WU Xiaoqian, HU Liangjian. Numerical Analysis and MatLab Experimental [M].Beijing: Tsinghua University Press, 2004:20-30.

Dynamic tension analysis on winding yarn in jacquard deviceof tufting carpet machine

XIA Shenghua, SUN Yize, MENG Zhuo, REN Guobin

(SchoolofMechanicalEngineering,DonghuaUniversity,Shanghai201620，China)

Tension control of carpet tufting loom yarn is a key factor influencing the jacquard quality. For the effective control on it, the paper focuses on the impact of stepper motor′s input for the jacquard yarn tension variations. Firstly, dynamic model of the stepper motor jacquard device was created and the correspondence between the input angular frequency and the output torque was analyzed. According to the improved Euler equation, the yarn dynamic tension model was established, in which the section of yarn was around the jacquard roller. Meanwhile， the mathematical model of the stepper motor and the yarn dynamic tension model of the jacquard device were further analyzed. Under the different initial conditions of jacquard roller radius, center distance, yarn wrap angle and so on, its value changes were analyzed by the method of iteration-Euler, the quantitative relationship between the input angular frequency and the output yarn tension was derived and the effect of different corners to the dynamic tension of the yarn was researched. This is a reference to the manufacturing and research of different high pile tufted carpets and even the full-scale jacquard tufted carpet.

tufted carpet; jacquard device; yarn tension; stepper motor; iteration-Euler

2014-05-30

2014-09-21

国家自然科学基金资助项目(51175075，51375084)；教育部创新团队发展计划资助项目(IRT1220)

夏胜华(1987—)，男，硕士生。主要研究方向为簇绒地毯织机满幅提花设计与优化。孙以泽，通信作者，E-mail: sunyz@dhu.eu.cn。

10.13475/j.fzxb.20140505606

TS 103.3；TS 103.7

A