应用广义Julia集图形的服装纹样设计方法
2015-06-10贾凤霞
贾凤霞, 张 聿
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 浙江省服装工程技术研究中心, 浙江 杭州 310018)
应用广义Julia集图形的服装纹样设计方法
贾凤霞1,2, 张 聿1
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 浙江省服装工程技术研究中心, 浙江 杭州 310018)
为探讨服装纹样设计的新方法,首先通过叠加多项式函数进行Julia集数学模型的函数变换,获得一类造型独特的新型Julia集图形,然后根据服装流行趋势,结合所得Julia集图形确定设计灵感源与主题,通过截取该Julia集图形的元素,运用Photoshop等图形软件进行二次设计,重构可充分表达设计主题的服装纹样,同时采用数码技术实现丝绸面料印花。在此基础上,选择可与纹样设计主题契合的服装款式进行服装整体设计与制作,结果表明,应用广义Julia集图形进行服装纹样设计是可行的。
广义Julia集图形; 服装纹样; 面料印花; 设计方法
Julia集图形是在复域上建立数学模型,经计算机处理生成的复杂而具有未来感的分形图形。其构图与造型根据不同的数学模型千变万化,非人类大脑所能想像。
近年来,将分形图形应用在服装设计中已取得一定的成效。文献[1-3]研究了几类典型分形图形的结构特点,并结合服装设计软件,将分形图形应用到服装图案的设计中;夏伶俐等[4]着重讨论了规则的Julia 集图形在服饰图案设计中的应用;张聿等[5-6]结合数字喷墨印花工艺,对分形图案在服饰图案设计上的应用方法等进行了研究。另一方面,关于运用函数变换等方法探讨分形图形变化途径的文献不断涌现,文献[7-8]对Julia等分形集的数学模型变换以及由此生成广义分形图形的方法进行了讨论。然而,根据流行趋势,针对系列化服装的纹样设计应用,采用特殊的函数变换方法生成适用的图形进行服装纹样设计方面的研究则鲜有报道。本文以广义Julia 集为研究对象,基于计算机实验确定在Julia集数学模型中叠加多项式函数的一种具体方法,并探讨运用由此方法生成的一类新型图形进行系列化服装设计与制作实践的具体途径。
1 广义Julia 集图形的生成原理
1.1 新型Julia集图形的数学模型
Julia集(以下简称J集)图形的产生原理是在复平面上考虑一个迭代过程[9-11]:
(1)
式中:z=x+yi,z为复函数,x、y为变量;i为虚数;μ=p+qi,μ为复常数,p、q均为常数。当μ值固定时,给定复数z0作初始值,进行迭代运算,运用计算机方法可绘出规则的J集图形。
1.2 广义Julia集图形的变换方法
为获得更多类型的J集图形,需通过函数变换产生新型的图形。本文研究运用叠加的方法进行函数变换,主要包括以下几种类型。
1)叠加三角函数,即在数学模型中叠加三角函数使图形发生变化。例如,分别在J集数学模型中叠加正弦函数:

(2)
式中a为可调参数。
同时,考虑选用RGB色彩模式(以下均用此模式),由此获得一类广义J集图形,如图1所示。其中:图1(a)的a、p、q取值分别为a=0.5,p=-0.76,q=-0.1;图1(b)的a、p、q取值分别为a=0.01,p=0.317 17,q=-0.027 27。
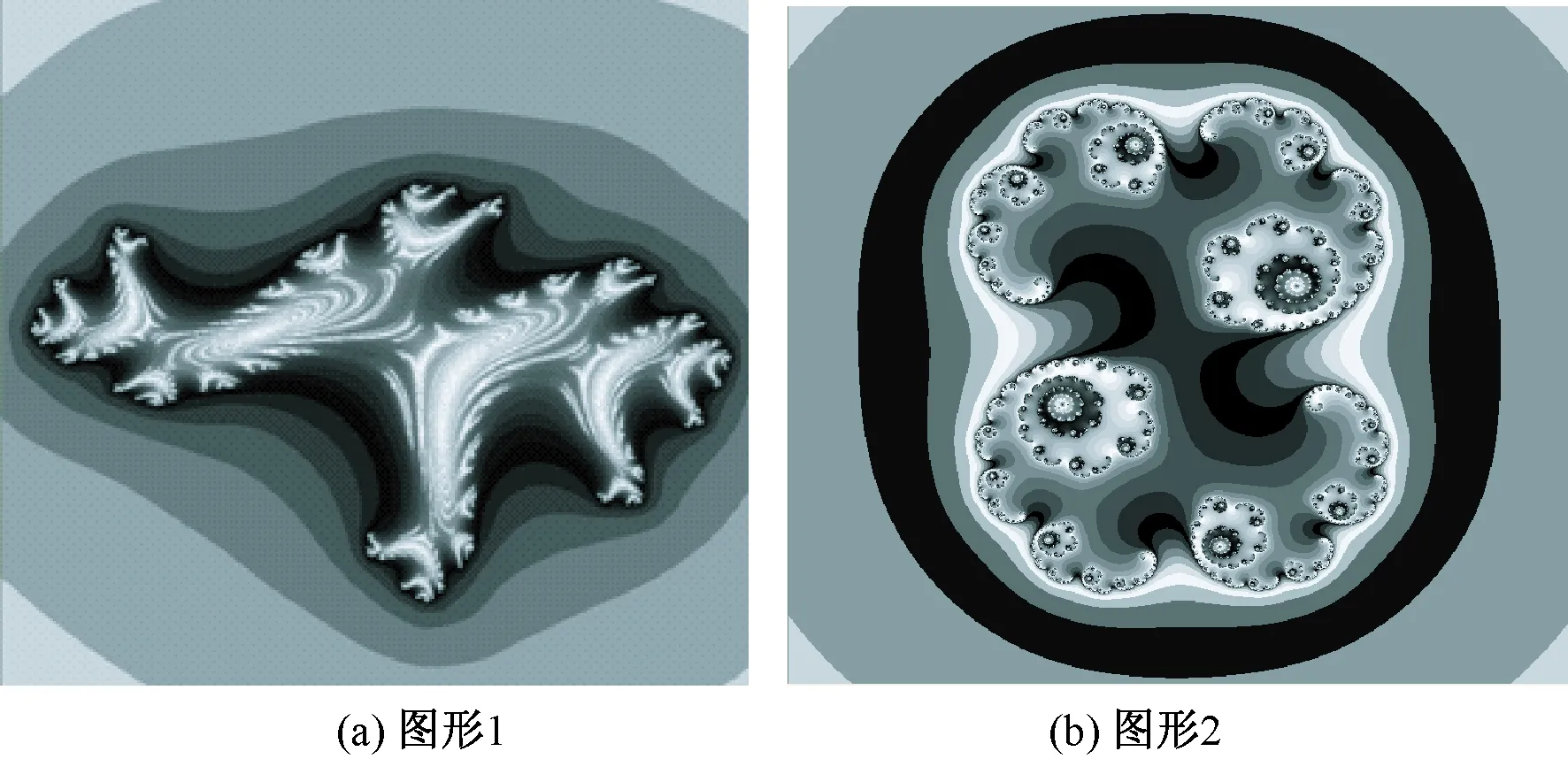
图1 叠加正弦函数的J集图形Fig.1 Julia set graphics of superimposed sine function. (a) Graphic 1; (b) Graphic 2
2)叠加多项式,即在数学模型中叠加多项式使图形发生变化。例如,分别在J集数学模型中叠加函数:
f(x,y)=ax+by+c
(3)
式中a、b、c均为可调参数。
由式(3)获得的广义J集图形如图2所示。图2(a)中a=0.15,b=0.15,c=0.001,p=-0.194,q=0.656;图2(b)中a=0.035,b=0.02,c=0.001,p=-0.88,q=0.31。

图2 叠加多项式的J集图形Fig.2 Julia set graphic of superimposed polynomial. (a) Graphic 1; (b) Graphic 2
2 广义J集图形的设计应用方法
2.1 广义J集图形的纹样设计应用方法
广义J集图形在服装纹样设计的应用总体上可分为直接应用和创新设计应用。直接应用是指将J集图形元素与构图等比较完整地应用于服装纹样设计中的一种设计方法;创新设计应用则是指运用解构、重组图形元素等手法进行创作设计。
直接应用主要是针对其色彩、构图、造型、风格等方面均比较完善,可以相对完整地直接作为服装纹样应用而言。要点是根据服装装饰部位的形状、位置及服装整体风格所需,有选择地直接截取相应的图形,通过简略的拼接等处理进行纹样设计。图3示出J集图形元素拼接组合过程。在以神秘黑色和科幻蓝色为主色调的渐变J集图形中,图形元素犹如散落着大大小小闪烁的星星,有的三五成群似星座,有的团抱一起呈星云状,这类图形完全可以通过复制、拼接等手法得到新的图形应用于服装设计中。首先对原图作镜像处理,然后将原图与镜像处理后的图拼接,得到首次拼接图1,采用同样方法重复操作即可得到拼接图2和需要的新图。

图3 J集图形元素的拼接组合过程图Fig.3 Combination of Julia set graphics elements. (a) Original graphic; (b) Spliced graphic 1; (c) Spliced graphic 2; (d) New graphic
创新设计是纹样设计创作中另一重要方法。重点在于将原有J集图形的形象打散,然后重新组合,形成一种新的结构形态或形象,即通常所说的解构重构。解构的方法可以是纵向或横向分解、等分分解、按结构分解、按角度分解等规律性的解构;也可以是将对象随意解构、拆散等自由分解。解构后,再以一定的形式如交叉、重叠、反向、反复、随意排列等将解构的元素重新进行组合,构成新的图形,如图4所示。图4(a)为原图,将原图自由分解出多个元素,然后按照协调、平衡形式美法将它们重新组合构成新图,新图的层次更加丰富。

图4 打散重构的J集图形Fig.4 Scattered and reconstructed Julia set graphics. (a) Original graphic; (b) New graphic
2.2 具体设计实践步骤
由美国流行资讯网(StyleSight)发布的2015年春夏流行趋势可知当季共有4大主题:和谐(harmony)、冲动(impulse)、记忆(memory)、核心(core)。本文以和谐主题为例,阐释应用广义J集图形进行服装设计实践的具体方法。
确定以诠释自然的和谐主题为选题方向设计制作一个系列的服装:科幻星空。
设计思路:和谐主题致敬大自然,在自然景观的启发下,打造新式设计,讲述关于自然的全新故事。纯粹的醇厚色调,体现着大自然的神圣;面料材质富有触感,各种天然元素新颖、协调,散发着自然气息,流露出原生态的优雅感;面料纹样模仿大自然的纹理,诱人碰触,展现着自然界的美感;款式设计强调以下元素:“V”字活力领型、斗篷衣袖、腰部褶裥、叠层造型、新颖结构性色块镶拼、弯形滚边细节、前高后低的“凹”状不对称设计、修身喇叭廓形裙摆等,都为经典原型注入新颖感觉。
设计制作过程可概括为以下步骤:确定灵感源—设计定位—生成与选取特定的广义J集图形—运用 Photoshop等绘图软件进行二次设计—结合主题进行服装款式、图形、材料、制作工艺等的整体设计构思,绘制服装设计效果图—制作实践。
2.2.1 灵感源
科幻星空系列灵感来自自然界的神秘星空,见图5。表达致敬自然,探索宇宙的理念,用纯粹、柔和的天然色调,不对称轮廓造型和层次丰富的数码印花技术为服装增色。

图5 神秘星空图片Fig.5 Mysterious sky picture
此系列诠释星空,致敬宇宙,从印花元素到配饰,充分利用源自星空的素材,如流星、星云、黑洞等,令人遐想。
2.2.2 设计定位
主题目标人群以一、二线城市年龄在30~45岁之间有一定经济实力的中高端女性消费者为主,她们优雅时尚,品味成熟,独立自信,事业有成。选择质地舒适的面料,个性鲜明的纹样,突出肩部的简明轮廓造型,可彰显这一消费群体的与众不同。
2.2.3 选取特定的广义J集图形
选取图3(a)带有宇宙星空效果的广义J集图形,截取其中部分元素作为设计素材。该图形独具的光感、质感,加上错落有致的排列效果,有力地彰显了宇宙星空的科幻、神秘之美,传达出人们探索宇宙奥秘、追求自然真相的精神。
2.2.4 二次设计
利用Photoshop绘图软件对图3(a)所示的广义J集图形素材进行四方连续和色彩调整处理。该系列中4个款式的纹样均为定位图形纹样,款式1~3均采用图6(a)所示的印花纹样1,款式4采用图6(b)所示的印花纹样2。
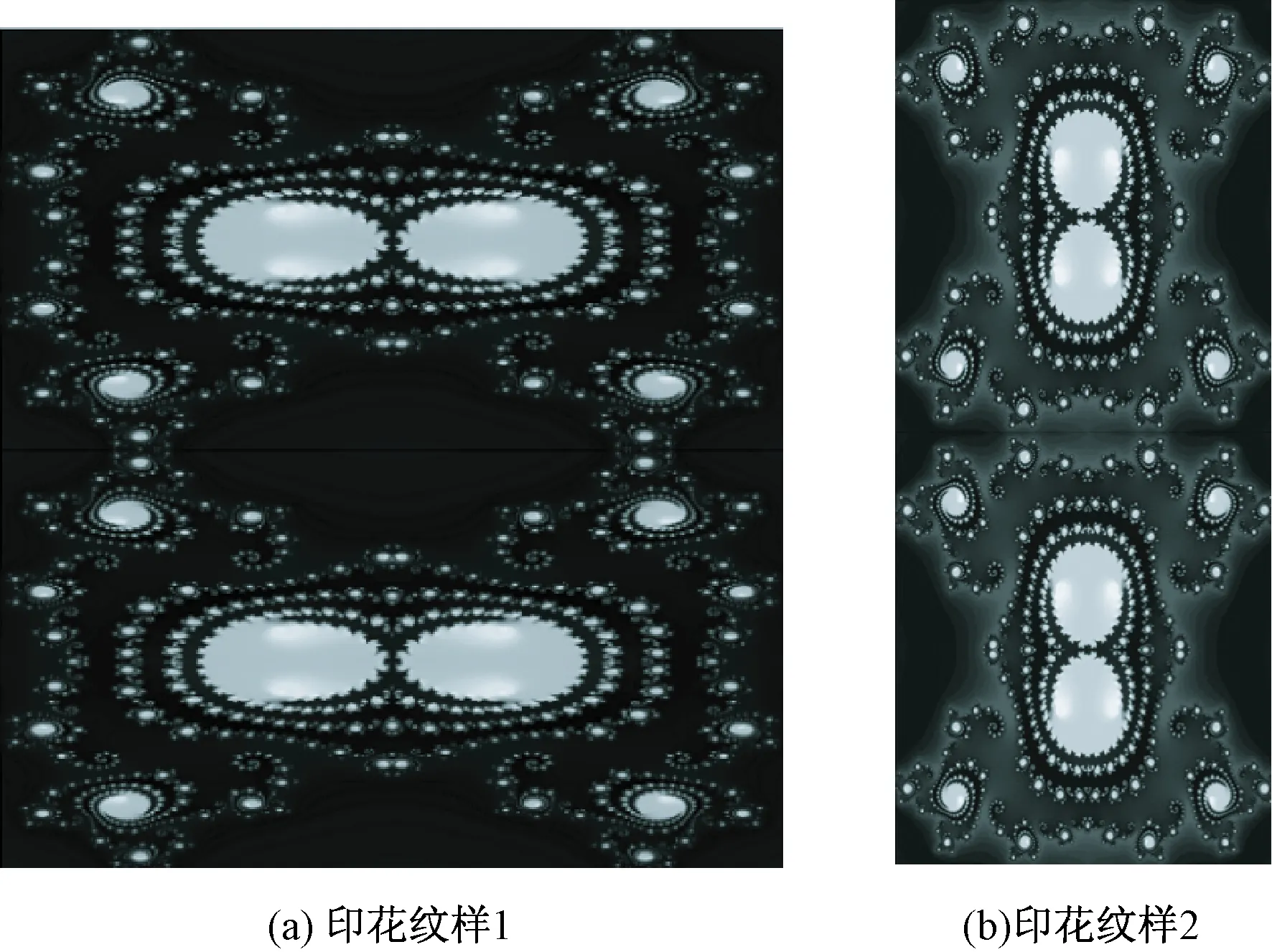
图6 科幻星空主题印花纹样Fig.6 Printing patterns of science fiction star theme. (a) Printing pattern 1;(b) Printing pattern 2
2.2.5 绘制服装设计效果图
根据流行趋势,绘制服装设计效果图,见图7。

图7 科幻星空主题服装效果图Fig.7 Fashion rendering of science fiction star theme
2.2.6 服装款式设计
根据流行趋势,绘制科幻星空系列设计正背面款式结构图,如图8、9所示。
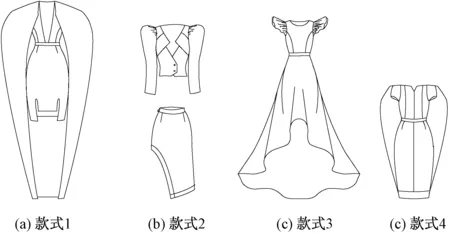
图8 科幻星空主题正面款式结构图Fig.8 Style front structure diagram of science fiction star theme. (a) Style 1; (b) Style 2; (c) Style 3; (d) Style 4

图9 科幻星空主题背面款式结构图Fig.9 Style back structure diagram of science fiction star theme. (a) Style 1; (b) Style 2; (c) Style 3; (d) Style 4
2.2.7 制作实践
科幻星空主题系列的设计步骤包括:CAD制版—白坯布样衣试制—样衣试穿、修改—局部修改、调整—相应的CAD样板修改、调整—面料进行数码印花—排料、裁剪—成品服装缝制—后期处理。
为突出该系列未来感、科幻感及星星应有的闪烁光感,根据图形大小、位置,采用丝线手工缝制黄色亮片,其效果如图10所示。

图10 手工缝制亮片照片Fig.10 Photo of hand stitched sequins
2.3 设计实践效果
经过上述步骤制成了成品服装,模特着装展示效果如图11所示。

图11 成品服装照片Fig.11 Finished clothing photos. (a) Finished clothing 1; (b) Finished clothing 2; (c) Finished clothing 3; (d) Finished clothing 4
3 讨 论
应用新型J集图形进行服装纹样设计实践,影响其最终设计制造效果的因素较多,除设计上的主观因素外还有客观因素。
3.1 广义J集图形的主要影响因素
影响生成新型J集图形的主要因素包括叠加函数表达形式、参数以及色彩模式的选择等。具体有:
1)叠加函数的形式。从式(2)、(3)可见,在生成广义J集图形时,叠加函数形式的选择对于图形造型起决定性的影响作用。将式(2)中的正弦函数换为余弦函数时,即f(x,y)=acos(x+y),如果p、q不变,取a=0.007 5,图形将分别呈现图12所示的造型。所以,叠加函数具体形式的选择需要结合生成图形的计算机实验进行取舍。
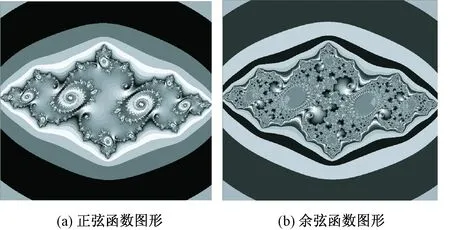
图12 不同函数对应的图形Fig.12 Different graphics with different functions. (a)Sine function graphic;(b)Cosine function graphic
2)参数的选择。由其数学模型的特点所决定,J集图形的参数影响首先来自源生参数p、q。在此基础上,从式(2)、(3)可见,在确定广义J集图形的叠加函数形式后,式(2)的a及式(3)中的a、b、c等参数对生成的图形影响极大。例如,在式(3)中,如果函数的形式及参数p、q值不变,取图2(b)的a、b、c置换图2(a)的a、b、c参数,可得到与图2(a)对比的图形(见图13),可见a、b、c参数对J图形影响很大;此外,对比图1(a)与图12(a)亦可同样说明参数对J图形的影响。因此,如何通过计算机实验确定其他参数进行配合生成满意的图形也非常关键。

图13 置换参数的图形Fig.13 Graphics with substituted parameters
3)色彩模式的选择。计算机上可选择的色彩模式较多。其中,RGB色彩模式的图形具有色彩丰富,过渡细腻等特点,视觉效果突出,但其他色彩模式均有其独自的特点与独特的应用,所以,模式的选择取决于设计的考虑与技术实现的要求。为了降低成本,需要选用平网印花,则可选用Qbcolor等模式更加方便分色处理。
3.2 服装纹样设计的主要影响因素
从上述分析可见,服装纹样设计的影响因素除来自J集图形外,还受流行趋势、技术手段客观因素以及设计者自身的设计经验、思路等主观因素的制约。从客观因素看包括以下几个方面。
1)流行趋势。流行趋势的形成,一方面来自权威机构的信息,另一方面来自对市场销售现状的判断。对于具体的设计而言,如何根据这些信息作出自己的判断,找到合适的灵感源,挖掘合适的主题进行设计完全取决于个人的经验与素质。
2)技术手段。主指设计手段与技术实现手段的提升与创新对纹样设计有重要影响。
设计手段方面:如本文研究的数字图形生成手段,实现图形二次设计的图形处理软件以及服装CAD设计软件等方面的进步与提高都为服装纹样设计拓宽了创新、创意设计的空间;技术实现手段方面,如数码印花、数码提花与数码绣花等加工手段的形成,以及新的面料材料与加工技术等不断涌现,均为服装的设计制作提供了新的条件,把以前不敢想的变为现实,从而赋予了全新的服装设计制作理念。
4 结 论
1)本文通过选择合适的叠加多项式函数进行J集数学模型的函数变换,借助计算机手段生成一类造型独特的广义J集图形,并根据服装流行趋势,进行服装纹样设计与制作实践,证明应用广义J集图形进行服装纹样设计的方法,为服装设计提供了理论依据。
2)叠加函数表达形式、参数以及色彩模式的选择等因素对广义J集图形的生成影响较大,在具体设计过程中要结合计算机实验,根据服装流行趋势与设计总体思路综合考虑与把握。
3)设计手段与技术实现手段的进步虽然为服装设计制作拓宽了创作的空间,但对这些手段与工具的合理运用及把握归根到底取决于设计者个人的技能、经验等综合素质,因此,如何学习掌握与运用数字图形等新方法、新技术是服装设计人员面临的一个重要课题。
FZXB
[1] 蔡燕燕.分形几何在服装图案设计中的研究与应用[D].上海:上海工程技术大学,2011:25-28. CAI Yanyan. Research and application of fractal geometry in clothing pattern design[D]. Shanghai: Shanghai University of Engineering Science,2011:25-28.
[2] 王淑颖.基于分形理论的服饰图案设计的研究与应用[D].无锡:江南大学,2010:35-43. WANG Shuying. The study and application of costumes design based on fractal theory[D]. Wuxi: Jiangnan University, 2010:35-43.
[3] 杨枝.分形图案在服装设计中的应用[D].北京:北京服装学院,2010:18-20.
YANG Zhi. The application of fractal patterns in costume design[D].Beijing:Beijing Institute of Fashion Technology, 2010:18-20.
[4] 夏伶俐.基于分形几何学理论的数字图形在时装设计中的应用研究[D].杭州:浙江理工大学,2011:36-49. XIA Lingli. Application research on digital graphics which based on the fractal geometry theory in fashion designing[D]. Hangzhou: Zhejiang Sci-Tech University, 2011:36-49.
[5] 张聿, 李玲,付岳莹. 基于IFS随机迭代算法的印花图案设计[J].纺织学报,2008,29(2):106-109. ZHANG Yu, LI Ling, FU Yueying. Fabric printing pattern design based on IFS random iteration algor-ithm [J]. Journal of Textile Research, 2008,29(2): 106-109.
[6] 窦晓静,张聿. 基于Mandelbrot集的仿扎染纹样设计方法[J].纺织学报,2012,33(7):82-87. DOU Xiaojing, ZHANG Yu. Design method of imitation tie-dye pattern based on Mandelbrot set [J].Journal of Textile Research, 2012,33(7): 82-87.
[7] 张聿,帅沁芬,付岳莹. 基于广义 Julia 集的印花图案设计[J].纺织学报,2007,28(4):82-86. ZHANG Yu, SHUAI Qinfen, FU Yueying. Printing pattern designing based on general Julia set [J].Journal of Textile Research, 2007, 28(4): 82-86.
[8] 姜会钰,郑春玲,刘素一. 基于分形理论中Mandelbrot集变换的印花图案设计[J].纺织学报,2010,31(12):139-142. JIANG Huiyu, ZHENG Chunling,LIU Suyi. Based on the fractal theory of Mandelbrot set transformation printing pattern design [J]. Journal of Textile Research, 2010,31(12):139-142.
[9] BARNSLEY M F. Fractals Everywhere[M]. New York:Academic Press Inc, 1988:86-92.
[10] 胡瑞安,胡纪阳,徐树公. 分形的计算机图像及其应用[M].北京:中国铁道出版社,1995:117-124. HU Ruian, HU Jiyang, XU Shugong. Fractal Computer Graphics and Its Application[M].Beijing:China Railway Press, 1995:117-124.
[11] 金以文,鲁世杰. 分形几何原理及其应用[M].杭州:浙江大学出版社,1998:93-120. JIN Yiwen, LU Shijie. Principles and Applications of Fractal Geometry[M]. Hangzhou: Zhejiang University Press, 1998:93-120.
Application of generalized Julia set graphics in clothing pattern design
JIA Fengxia1,2, ZHANG Yu1
(1.SchoolofFashionDesign&Engineering,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China;2.ZhejiangProvincialResearchCenterofClothingEngineeringTechnology,Hangzhou,Zhejiang310018,China)
For clothing patterns design, some methods using a type of generalized Julia set graphic is discussed in this paper. Firstly, the function transformations are made by adding polynomial to Julia set equations to obtain a new type of Julia set graphics with some unique features. Secondly, according to the analysis on fashion trend, combining the inspirations from the Julia set graphics with the design theme, a redesign for clothing patterns with Photoshop or other graphic software by use of some elements in the Julia set graphics are made, which could express the design theme adequately. The printing of these patterns on silk with the digital spray printing machine are accomplished. Based on this, the overall designs and productions of fashions are carried out by choosing fashion style in accordance with the pattern theme. It is proved that the methods applying a type of generalized Julia set graphics to clothing pattern design discussed in this paper are feasible.
generalized Julia set graphic; clothing pattern; fabric printing; design method
2014-08-25
2015-03-10
浙江省重点科技创新团队项目(2011R50004);杭州市企业高新技术研发中心项目(20111131P16);浙江省服装工程技术研究中心开放基金项目(2015YXQN16)
贾凤霞(1978—),女,实验师,硕士。主要研究方向为服装设计与工程。张聿,通信作者,E-mail:hzzy11111@163.com。
10.13475/j.fzxb.20140804806
J 523.5; TS 941.2
A
