基于可控谐振电感技术的移相全桥变换器

姬军鹏，胡雪利，华志广，曾光，陈桂涛

（西安理工大学自动化与信息工程学院，陕西西安710048）

移相全桥PWM（pulse width modulation）控制方法常被用在中大功率开关变换器的设备中［1-2］，该控制策略中滞后桥臂不易实现软开关，并对负载电流有依赖性，这使得开关管的损耗增加，电磁干扰变大，占空比丢失严重［3-5］。利用开关管的寄生电容和变压器漏感之间的谐振来实现软开关是一种常用方法，但该方法的谐振点不易控制，ZVS的实现范围比较小［6-7］。在变压器原边增加2个开关管可以增大变换器软开关的实现范围，但这会增加开关管的导通损耗［8］。增大变压器的漏感会使滞后桥臂的软开关实现范围增加，但这会导致占空比的丢失和变压器原边的导通损耗增加［9-11］。本文提出一种新型的可控谐振电感技术，该技术中的可控谐振电感值根据负载电流的大小自动调节，减小了零电压开关（zero voltage switch，ZVS）实现过程中对负载电流的依赖性，减小了开关管操作过程产生的电磁干扰，提高了电源总效率，在减小占空比的丢失方面有较大的优势。本文利用软件仿真，验证了利用可控谐振电感技术轻松实现滞后桥臂的软开关。最后搭建了一台20 kHz，30 kW 的带可控谐振电感的高频逆变弧焊电源样机，轻载下实现了滞后桥臂的ZVS。对该样机进行了效率和传导EMI测试，与不带可控谐振电感时相比，轻载下效率得到提高，传导EMI大幅降低。实验结果验证了所提出技术的正确性。

1 电源系统设计

系统实现框图如图1 所示，主电路部分如虚线框中所示，主要由三相不控整流电路、全桥逆变电路、高频变压器和高频整流滤波电路组成。控制部分由高精度英飞凌单片机实现全数字化恒流控制［12-13］。

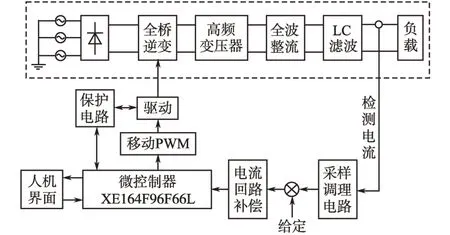
图1 变换器系统实现结构框图Fig.1 Converter system implementation block diagram

1.1 硬件电路设计

1.1.1 全桥逆变电路

全桥逆变电路的作用是把直流电压逆变为高频交流方波。逆变开关控制方式决定了电源的性能，控制精度决定变换器输出电流的控制性能，进而决定焊接质量。逆变电路需要实现软开关来降低开关损耗，进而提高电源效率，同时降低电磁干扰的产生，其电路拓扑如图2 所示。其中，L为可控谐振电感。

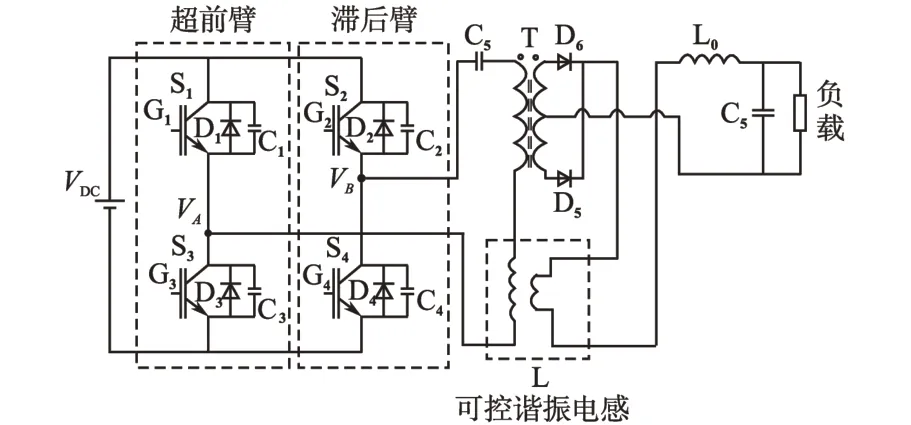
图2 弧焊逆变电源主电路拓扑Fig.2 Main circuit topology of inverter arc welding power supply

1.1.2 高频变压器

高频变压器既是能量传输的载体，又起到隔离和变压的作用。有源桥式变换器需要高频变压器来获得特定的绕组漏电感［14］。最大限度地减小铜损和磁芯损耗以达到高效的目的，有效的窗口面积限制了变压器绕组的排列，本文的变压器工作在高频大功率场合，磁芯采用磁通密度较大的超微晶材料，以增加功率密度，采用具有低漏感的原边线绕和副边通体面绕的结构。

1.1.3 高频整流电路RC吸收电路的设计

次级整流二极管并联RC吸收电路用来抑制由变压器原边等效电感及二极管本体电容产生的电压尖峰及振荡，以减少电磁干扰。二极管承受的最大反向电压Vrmax为

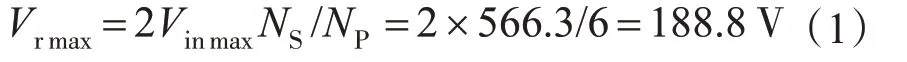
式中：Vinmax为变压器原边输入电压最大值；NS为变压器副边绕组匝数；NP为变压器原边绕组匝数。

查找数据手册，当二极管承受的最大反向电压Vrmax为200 V时，其结电容Cf取300 pF，设计时选吸收电容为快恢复二极管结电容的10倍，则可计算得吸收电容C为

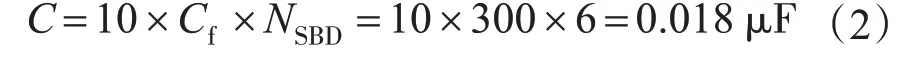
式中：NSBD为快恢复二极管并联的数量。

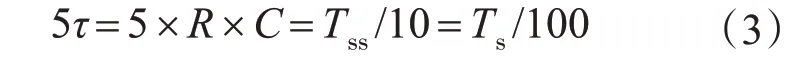
式中：R,C分别为吸收电路的电阻值、电容值；τ为RC吸收电路的时间常数。

由此可知，吸收电阻：

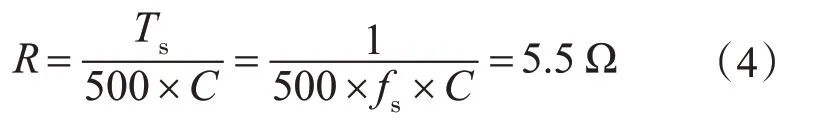
式中：fs为开关频率。

吸收电路中选取无感电阻与电容，电阻阻值R取6.67 Ω，电容容值C取0.04 μF。

1.1.4 驱动电路

本文的IGBT 驱动电路，主要采用2SD315A驱动模块进行设计，该驱动模块内设置了两组独立的驱动电路，而且模块内还包含了所需的驱动电源［15］。该模块可驱动1 200 V和1 700 V的IGBT，具有短路和过流保护的功能，峰值驱动电流可达±15 A。为了减小电磁干扰，提高信号传送质量，驱动电路中利用光纤进行信号的传送。

1.2 软件设计

移相全桥控制技术具有效率高、损耗低等优点，在谐振电感作用下可以实现4 个开关器件的ZVS。基于英飞凌单片机控制器设计4 路PWM时序控制图如图3所示［16］。

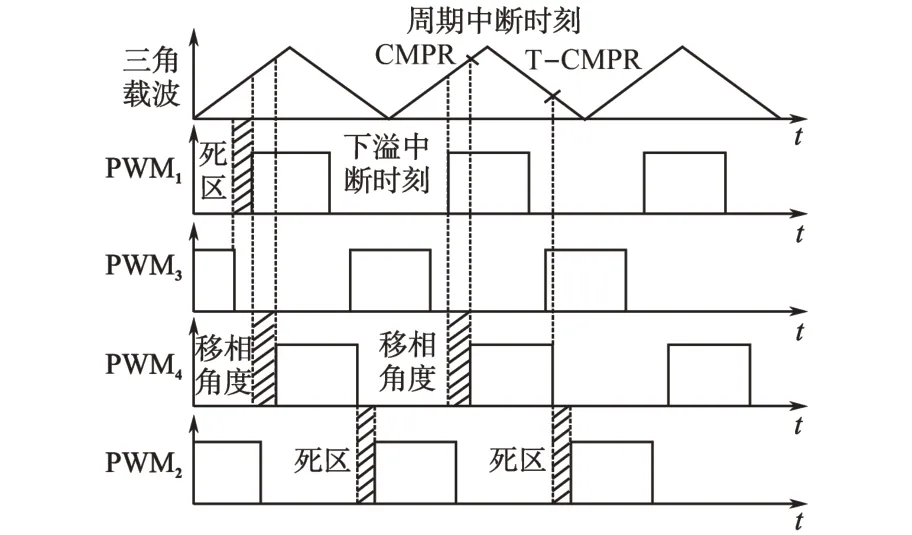
图3 移相全桥PWM生成原理图Fig.3 Schematic diagram of PWM generated in phase-shifted full-bridge

对图3 移相全桥PWM 生成原理进行分析，通过使用英飞凌单片机的CCU61 与CCU62 比较单元输出4 路PWM 方波，每个比较单元产生2 路带有死区时间的互补的PWM 信号。CCU61单元输出IGBT1与IGBT3所需脉冲，CCU62 单元输 出IGBT2与IGBT4所 需 脉 冲。CCU61 与CCU62 单元的比较寄存器的数值随调节程序在下溢中断与周期中断中不断修改。在下溢中断中赋给比较寄存器CMPR，在周期中断中赋给比较寄存器T-CMPR（周期值减去上次比较寄存器数值）。

2 可控谐振电感的设计与实现

2.1 原理及拓扑

本文所提出的可控谐振电感技术的拓扑结构如图2 中所示，该移相全桥ZVS 变换器由4 个IGBT 构成S1～S4，每个IGBT 都反并联1 个二极管D1～D4和1个缓冲电容C1～C4。全桥变换器输出交流电压，经过1 个隔直电容C5后连接1 个高频变压器T，可控谐振电感L 与变压器原边串联。后级采用全波整流和电感滤波方式，整流二极管为D5和D6，后级高频滤波电感和滤波电容分别为L0和C6。可控谐振电感的值由经滤波电感L0的输出电流控制，通过调节谐振电感的值，可以实现移相全桥变换器的ZVS，减小电磁干扰。由于移相全桥变换器的超前桥臂易实现ZVS，滞后桥臂不易实现，本文重点研究滞后桥臂的软开关实现。移相全桥变换器的控制脉冲时序及开关管端电压波形如图4所示［11］。

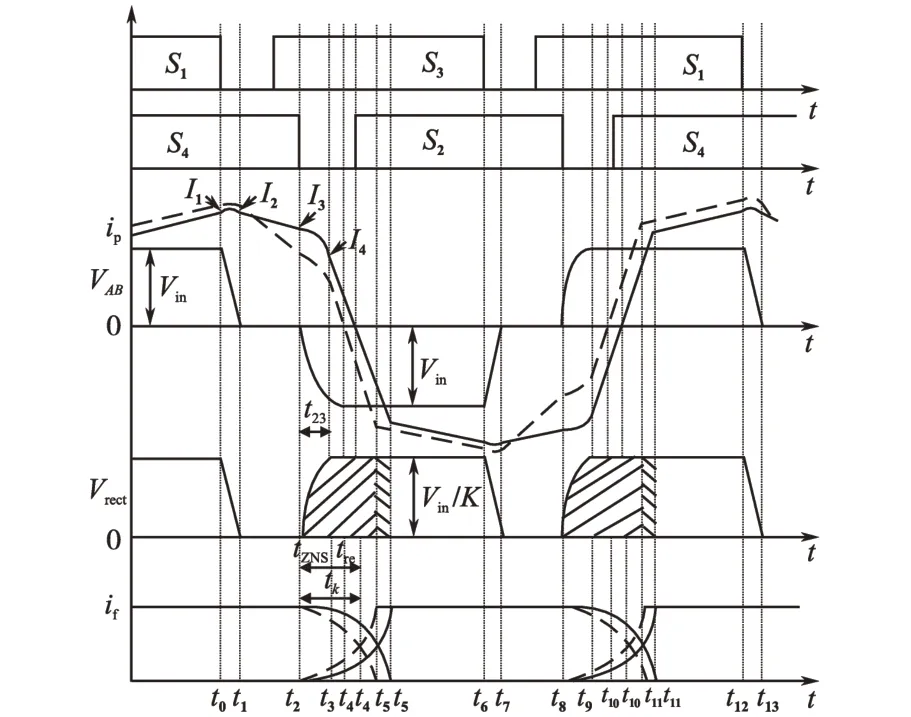
图4 移相全桥变换器控制脉冲时序图Fig.4 Time diagram of phase shifted full bridge converter

图4 中，S1和S3为超前桥臂的驱动信号，S2和S4为滞后桥臂的驱动信号。VAB为变压器原边电压，ip为变压器原边电流，if为后级滤波电感的电流。由于变压器绕组等效电阻的存在和开关管的正向压降过大，使得滞后臂实现ZVS的有效时间明显缩短，电路工作在非理想条件下，图4中实线表示不考虑等效电阻和导通压降的理想情况，虚线表示实际非理想情况。

当t ＜t0时，S1和D2导通，当t=t0时，S1信号为低电平，滞后桥臂开始工作，此时滞后桥臂的等效电路如图5所示。

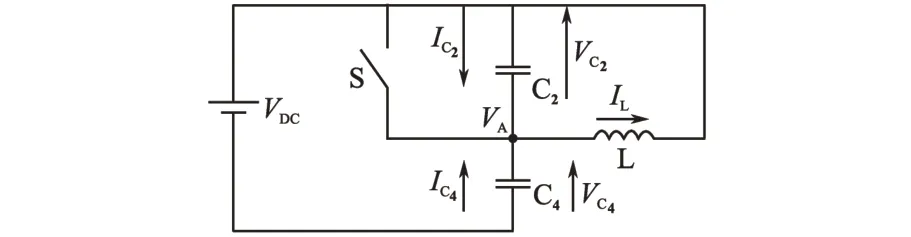
图5 滞后桥臂等效电路Fig.5 Equivalent circuit of the lagging arm

当t ＜t0时，开关S 是闭合的，此时电容C2两端电压VC2=0，电容C4两端电压VC4与直流母线电压VDC相等，即VA=VDC，后级滤波电感电流IL的初始值为IL(0)。当t=t0时，开关S 打开，电容C2和C4的电流IC2和IC4可表示为

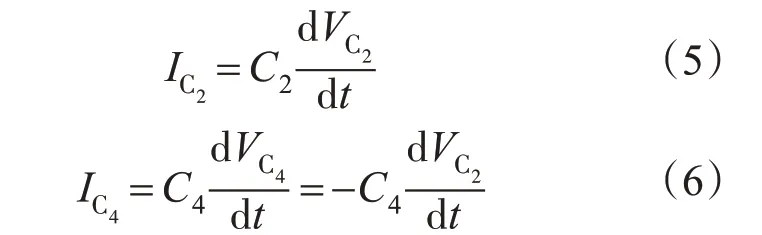
则可控谐振电感电流IL为

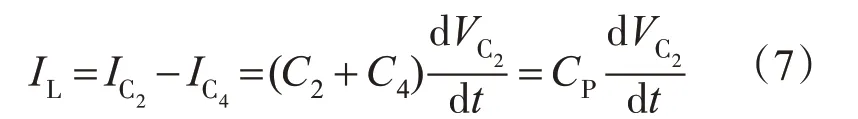
其中，CP为等效并联电容，可表示为

则串联LC谐振等效电路如图6所示。

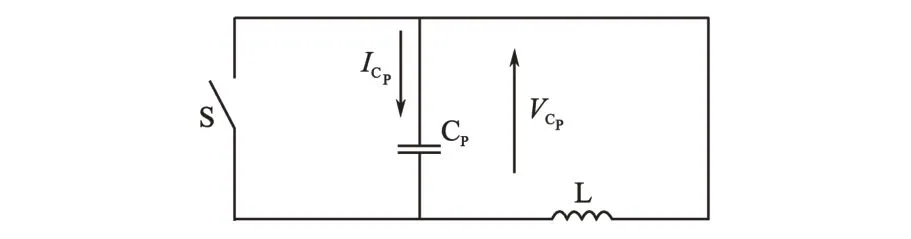
图6 串联LC谐振等效电路Fig.6 Equivalent circuit of series resonance LC

电感电流IL(0)和电容电压的初始值均为0，电路方程可表示为

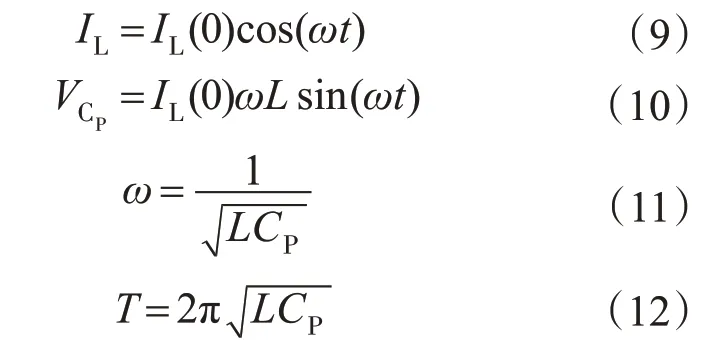
式中：ω为角频率；T为谐振周期。

在软开关的条件下，电感中应存储足够大的能量通过原边电流IP给等效并联电容CP充电，满足能量方程：

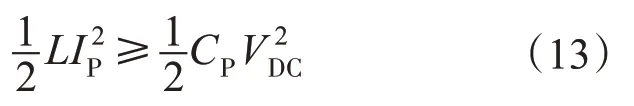
由式（13）知，满足ZVS 的原边电流最小值IPmin可表示为

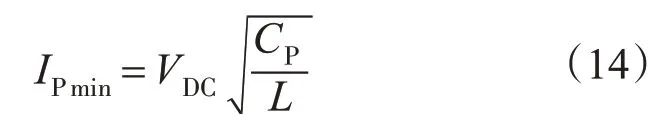
等效并联电容要完成1 次充放电，则原边电流应大于IPmin。

如果原边电流IP等于IPmin，由原边电流IP降为0，等效并联电容两端电压在1/4谐振周期时达到直流母线电压VDC，可计算其所需时间tZVS作为ZVS实现的最大时间tZVSmax：

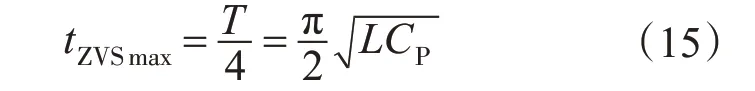
如果并联电容不能在tZVSmax时刻将能量完全释放，就不能实现软开关。

如果IP＞IPmin，等效并联电容电压VCP在tZVS期间从0上升到VDC，如果可控谐振电感电流的初始值IL(0)等于变压器原边电流初始值I3，tZVS可由下式计算：

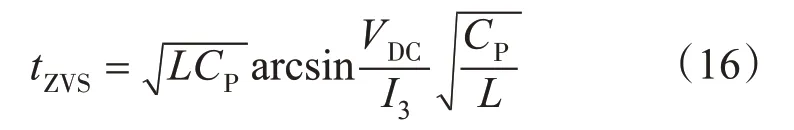
当IP从I3降到I4时，I4可由下式计算：

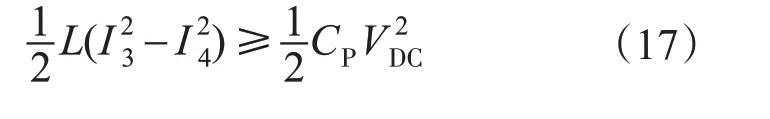
式中：I3，I4分别为t3和t4时刻变压器原边电流有效值。

当t=t4时，L两端开始承受负电压，电感电流在tre期间减为0，tre可由下式计算：

原边电流在tk=tZVS+tre期间降为0，在tZVS结束时，S2开始加脉冲，因此S1和S2之间的死区时间t23应满足下式：

因此，要使得负载电流在全范围内实现ZVS，则应满足式（19）。

2.2 可控谐振电感设计

本文所提出的可控谐振电感由2个相同的且不具有磁耦合的磁芯串联而成，变换器输出的直流电为可控谐振电感的控制绕组中的电流，控制电流在2个磁芯中产生一个直流偏置场。电感值大小随控制绕组匝数变化而变化，总体上随控制电流的增大而减小，可控谐振电感的变化范围为2～20 μH。在控制绕组没有电流时，可控谐振电感的值最大，可控谐振电感的大小由输出电流进行控制，在输出满载电流的0～1/4区间，可控谐振电感随输出满载电流变化较大；在输出满载电流的1/4～1/2区间，可控谐振电感随输出电流变化略微减小；在输出电流大于满载的1/2时，可控谐振电感随输出电流变化不明显。合理调节2个磁芯之间气隙大小，使得铁氧体磁芯的饱和范围变大。在较大的气隙条件下，磁芯的B-H曲线基本呈线性，气隙的选取应符合可控谐振电感的特性。

可控谐振电感的气隙大小的计算如下式所示：

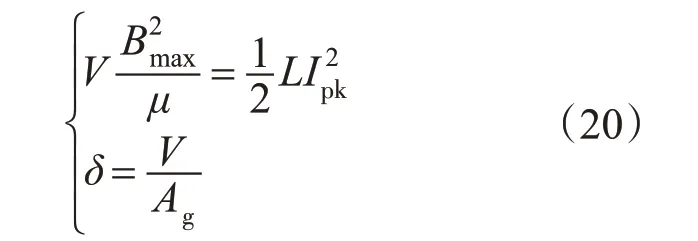
式中：V为全桥逆变输出电压有效值；Bmax为高频变压器磁通最大值；μ为铁氧体磁芯磁导率；L为输出电流为额定值时所对应的可控谐振电感值；Ipk为高频变压器原边电流峰值；δ为可控谐振电感气隙大小；Ag为有效导磁面积。

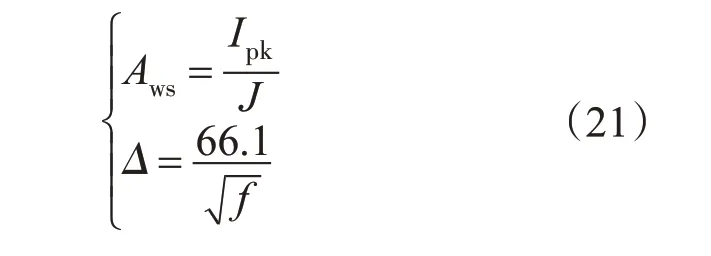
电感磁芯面积的计算如下式所示：式中：J为电流密度；Aws为集肤效应产生的集肤深度；Δ为可控谐振电感磁芯面积。

由式（20）得到可控谐振电感气隙δ的大小为4.23 mm；由式（21）得到可控谐振电感磁芯面积Δ为3.78 cm2。

3 仿真结果

3.1 输出电压和电流

满载时测得的输出电压和电流波形如图7 所示。

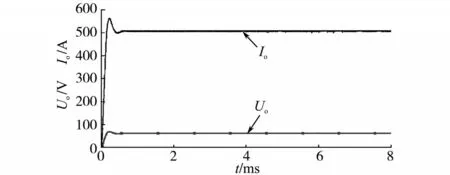
图7 输出电压电流波形Fig.7 Waveforms of the output voltage and current

由图7 可以看出输出电压Uo为60 V，输出电流Io达到500 A，纹波较小，满足设计要求。

3.2 软开关的实现

滞后臂的开关管S2和S4的仿真波形如图8所示。

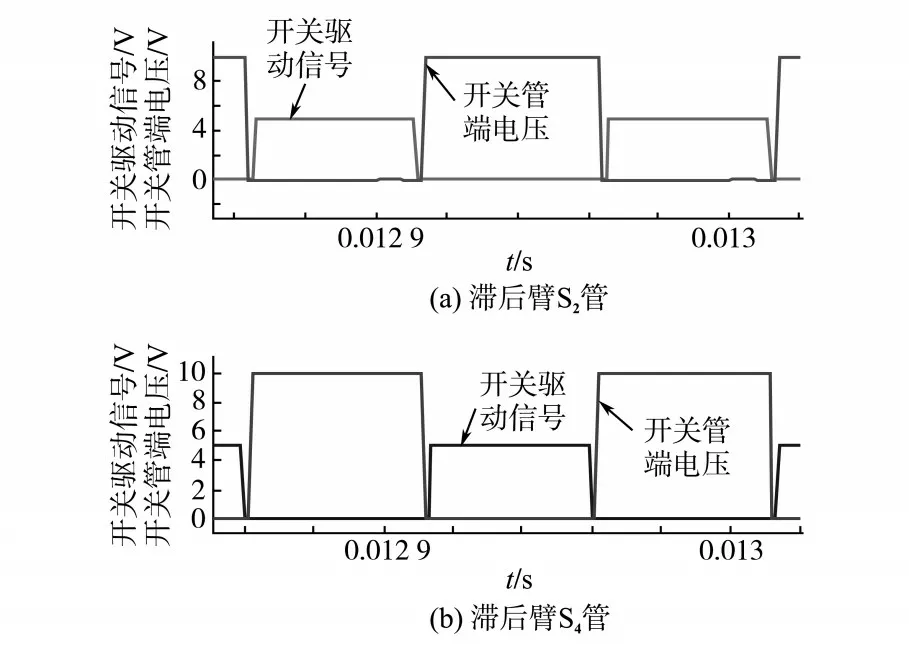
图8 滞后臂管压降及驱动波形Fig.8 Waveforms of the lagging arm tube voltage and drive signal

由图8 可知，开关管导通前滞后臂开关管两端电压已降为0 V，实现了ZVS。

3.3 RC吸收

RC 吸收电路中C=40 nF，R=2 Ω，R＝3.3 Ω，R＝4 Ω，R＝5 Ω，R＝6 Ω时的副边整流二极管电压波形如图9所示。

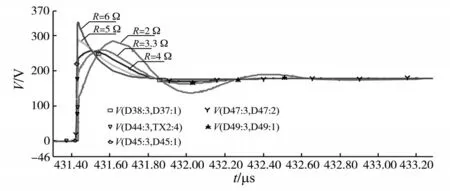
图9 副边整流二极管电压波形Fig.9 Waveforms of secondary side rectifier diode voltage

从图9可以看出，在R=4 Ω时为RC吸收电路的最佳效果。R＜4 Ω时副边整流二极管电压尖峰变大，振荡周期变长；R＞4 Ω时电压毛刺进一步增大，阻尼系数Q 变小，振荡周期变短。所以电阻值在4 Ω左右选取。

4 实验结果

4.1 高频逆变弧焊电源样机

利用移相全桥控制技术的原理搭建了1台功率为30 kW，60 V/500 A，20 kHz的高效高频逆变弧焊电源样机。

4.2 软开关的实现

在重载或满载条件下，移相全桥变换器的滞后臂ZVS 较易实现，但滞后臂不易实现，因此这里仅给出轻载状态下滞后臂的ZVS 波形。图10和图11 为25%负载条件下的滞后臂的ZVS 波形和变压器原边电压波形。

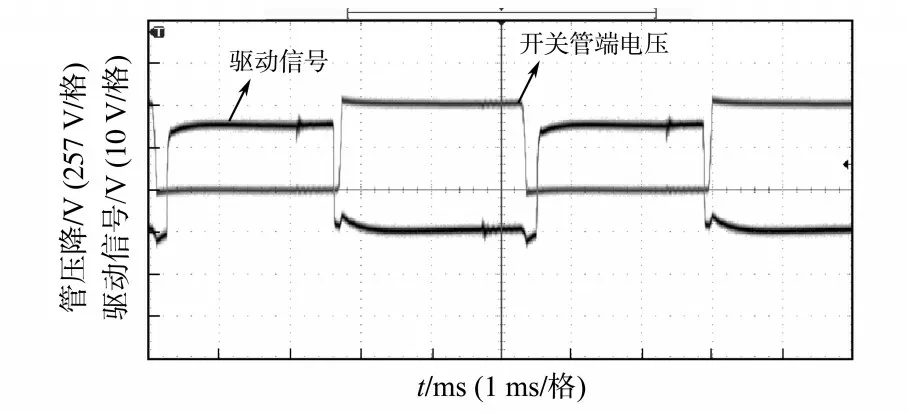
图10 2号开关管ZVS波形图Fig.10 No.2 switch ZVS waveforms

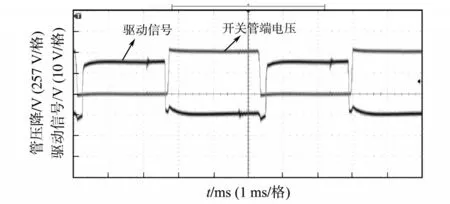
图11 4号开关管ZVS波形图Fig.11 No.4 switch ZVS waveforms

由图10、图11 可知，施加驱动信号前滞后臂开关管的管电压降已降为0 V，均实现了ZVS。

4.3 电源效率

带有可控谐振电感的弧焊逆变电源效率曲线如图12中实线所示，不带可控谐振电感的弧焊逆变电源的电源效率如图12虚线所示。

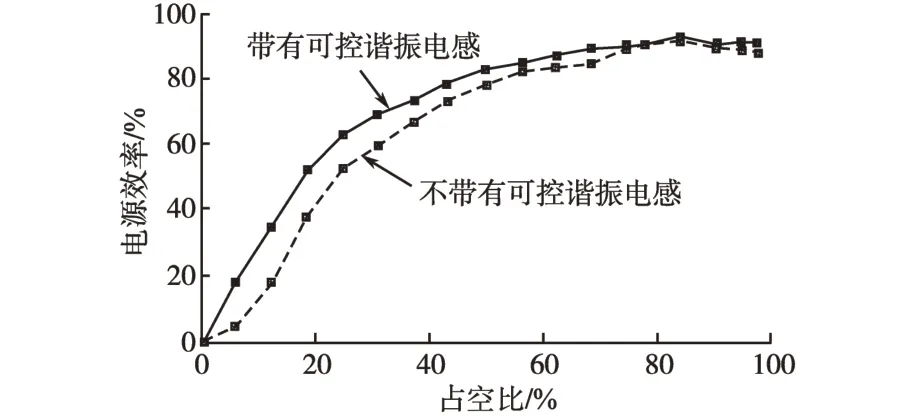
图12 电源效率曲线Fig.12 Power efficiency curves

由图12 可知，轻载时，由于谐振电感值由输出电流大小控制增大，滞后臂较易实现软开关，电源效率相对提高；重载和满载时，两者都能够实现软开关，效率基本相同。从总体上看，带有可控谐振电感电源的平均效率明显提高，占空比在0.5 以上时，电源效率可达80%以上，在满载时，电源效率可达到90%，所以提出的可控谐振电感技术大幅度提高了轻载运行状况下的电源效率。

4.4 传导EMI

对高频逆变弧焊电源样机进行共模传导EMI测试，测试原理框图如图13所示。

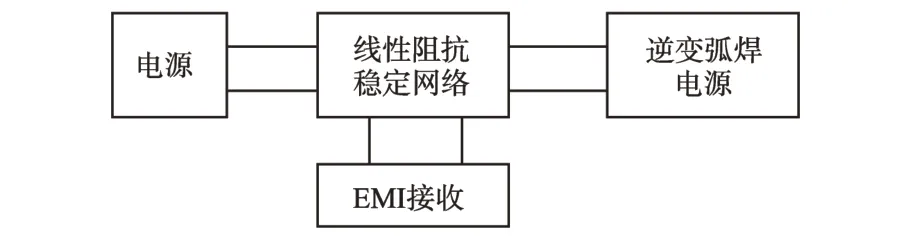
图13 传导EMI测试实现框图Fig.13 Realization diagram of the conducted EMI test

图13 中线性阻抗稳定网络可以为EMI 提供一个稳定的负载阻抗，并为EMI提供一个高频检测通路，滤除电网的高频噪声，减小测量误差。EMI接收采用频谱分析仪，可以接收到逆变弧焊电源的传导EMI信号。

采用可控谐振电感技术前后高频逆变弧焊机电源电网侧进行传导EMI测试，测试到的传导EMI频谱分别如图14和图15所示。

从图14 和图15 可以看出，未采用可控谐振电感技术的变换器低频段传导EMI 较大，可达70 dB·μV，中频段传导EMI也有60 dB·μV，平均幅值大约为45 dB·μV，干扰比较严重。利用可控谐振电感技术之后的传导EMI 在1 MHz 到30 MHz之间，EMI平均幅值在30 dB·μV周围，共模传导EMI有了明显降低。

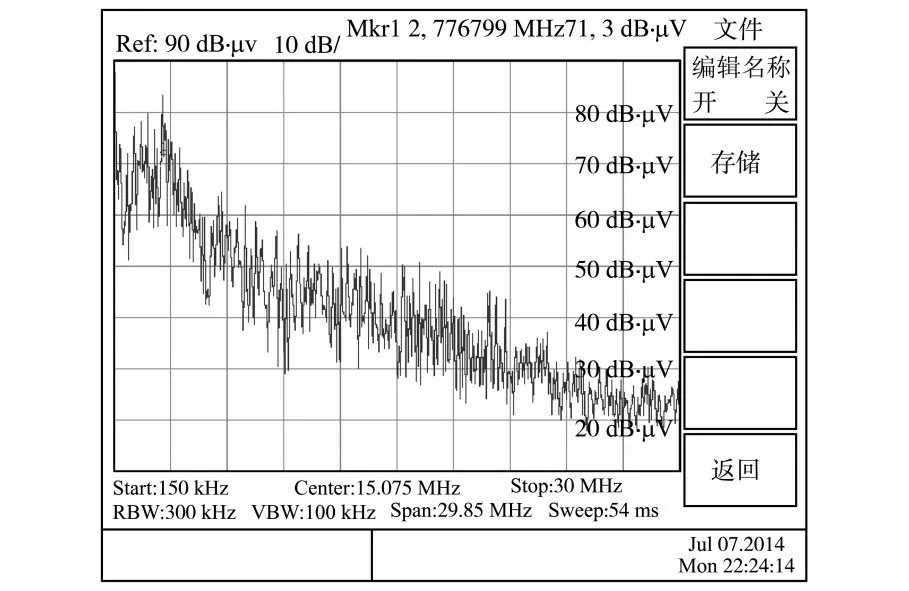
图14 未采用可控谐振电感时变换器共模传导EMIFig.14 The conducted EMI of converter without CRI

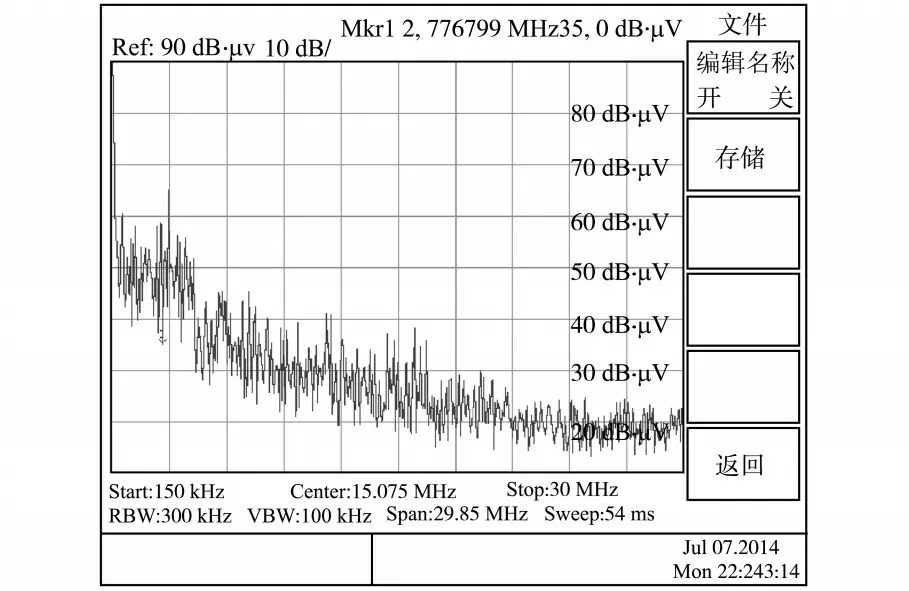
图15 采用可控谐振电感时变换器共模传导EMIFig.15 The conducted EMI of converter with CRI

5 结论

经过理论分析和实际调试，本文提出的可控谐振电感技术，可以容易地实现低压大电流高频逆变弧焊电源的软开关，减小了开关管操作过程中产生的电磁干扰，使得共模传导EMI 信号大大减小。在轻载情况下，可以通过增大可控谐振电感的值来获得软开关所需要的能量。在重载或满载情况下，可以减小寄生谐振和占空比的丢失。搭建了一台功率为30 kW，60 V/500 A，20 kHz的高效高频逆变弧焊电源样机，对该样机进行效率和传导EMI 测试，传导EMI 从未采用谐振电感技术的40～70 dB·μV 降到采用可控谐振电感技术之后的20 dB·μV，轻载效率得到明显提高，验证了所提出可控谐振电感技术的合理性和可实现性。

［1］ 陈仲，石磊，季飚，等.带辅助网络的倍流整流方式全桥ZVS 变换器［J］.中国电机工程学报，2010，30（30）：32-37.

［2］ Wang J M，Wu S T，Chiu H J.A Novel Energy-retaining Inverter for AC Arc Welding Machines［J］.Int.J.Circuit Theory Appl.，2012，40（2）：107-126.

［3］ 曹神抚，李彬.基于双环控制的电焊机逆变器的实现研究［J］.电力电子技术，2011，45（9）：105-107.

［4］ 孙铁成，李瑞，郭建辉，等.带辅助网络的倍流整流式全桥ZVS 三电平变换器［J］.电工技术学报，2008，23（8）：74-79.

［5］ 徐向华，张加胜，郝秀杰.一种新型的移相式全桥软开关变换器［J］.电气传动，2014，44（8）：27-30.

［6］ 孟培培，吴新科，张军明，等.新型磁集成零电压零电流软开关全桥变流器［J］.中国电机工程学报，2012，32（3）：15-21.

［7］ 孙铁成，汤建华，高鹏，等.一种新型全桥零电压转换PWM DC/DC 变换器［J］.中国电机工程学报，2006，26（6）：83-88.

［8］ 陈仲，刘沙沙，史良辰，等.两种加辅助网络的全桥变换器的损耗对比分析［J］.中国电机工程学报，2012，32（18）：66-72.

［9］ Emami Z，Nikpendar M，Shafiei N，et al.Leading and Lagging Legs Power Loss Analysis in ZVS Phase-shift Full Bridge Converter［C］//Power Electronics，Drive Systems and Technologies Conference.Tehran，Iran：IEEE，2011：632-637.

［10］Chen Z，Ji B，Ji F，et al.Analysis and Design Considerations of an Improved ZVS Full-bridge DC-DC Converter［C］//Applied Power Electronics Conference and Exposition.Palm Springs，USA：IEEE，2010：1471-1476.

［11］Jang Y，Jovanovic M M.A New PWM ZVS Full-bridge Converter［J］.IEEE Trans.on Power Electronics，2007，22（3）：987-994.

［12］Sun Qiang，Ji Junpeng，Tian Huan，et al.Design of Active Power Filter for Low Voltage and High Current Switching Power Supply［C］//Asia-pacific Power and Energy Engineering Conference，Wuhan China，2011.

［13］李钊，王国建，徐道恒，等.基于FPGA的移相全桥控制器数字化实现［J］.电气传动，2012，42（9）：33-36.

［14］石健将，罗劼，何湘宁.相同移相角控制的串-并型移相全桥组合变换器［J］.中国电机工程学报，2012，32（21）：23-30.

［15］和军平，姜建国.离线式PWM开关电源传导电磁干扰的分析研究［J］.中国电机工程学报，2003，23（6）：91-95.

［16］Djilali Hamza，Mei Qiu，Praveen K Jain.Application and Stability Analysis of a Novel Digital Active EMI Filter Used in a Grid-tied PV Micro Inverter Module［J］.IEEE Trans.on Power Electronics，2013，28（6）：2867-2874.