基于模糊参数优化的PMSM反推直接转矩控制

徐艳平，雷亚洲，马灵芝，沙登卓

（西安理工大学电气工程系，陕西 西安710048）

永磁同步电机（PMSM）直接转矩控制（DTC）具有控制方式简单、转矩响应快、便于实现全数字化的优点［1］，但是存在磁链和转矩脉动大，逆变器开关频率不恒定等缺点。

目前改善传统直接转矩控制系统性能的方法有矢量细分法［2-3］，占空比控制方法［4］和空间矢量调制方法［5］等。矢量细分法将基本电压矢量进行细化，根据电压矢量对磁链和转矩的作用，选择更为适合的电压矢量，但是矢量划分越细，控制就越复杂。占空比控制方法则是考虑零矢量的作用，确定出作用有效电压矢量的占空比进行控制，但是占空比的准确计算及控制难以达到。采用空间矢量方法可以达到减小磁链转矩脉动的目的，但这种方法中通常会使用PI 控制器来控制转矩性能，在一定程度上影响了系统的快速性。

反推控制方法［6］是针对不确定性系统的一种系统化的控制器综合方法，目前反推控制方法已经用于永磁同步电机控制中［7-8］。但是目前已有的用于永磁同步电机的反推控制方法，多集中在电机矢量控制和转速环控制中。本文将反推控制引入永磁同步电机直接转矩控制中，并采用模糊控制实现对反推控制器中参数的在线调节。

1 永磁同步电机的数学模型

PMSM在两相静止坐标系中的状态方程为

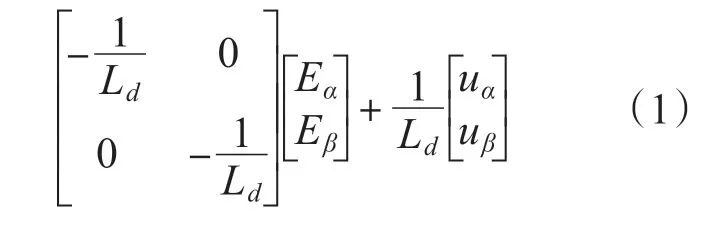
其中

式中：uα,uβ分别为定子电压在α,β 轴上的分量；iα,iβ分别为定子电流在α,β 轴上的分量；id,iq分别为定子电流在d,q 轴上的分量；Rs为定子电阻；Ld,Lq分别为电感在d,q 轴上的分量；ωr为转子角速度；Ψf为转子永磁体磁链；θr为转子角度。

PMSM 的电磁转矩方程、磁链方程、机械运动方程分别为

式中：Te为电磁转矩；np为电机极对数；Ψs为定子磁链的平方；Ψα,Ψβ分别为定子磁链在α,β 轴上的分量；J 为转动惯量；Bm为摩擦系数；TL为负载转矩。

2 模糊参数优化的反推DTC

2.1 反推控制器设计

对于永磁同步电机的直接转矩控制系统，定义转速误差为

针对直接转矩控制，选取电磁转矩和定子磁链为虚拟控制状态来控制电机转速。为了使速度误差趋于零，构造李亚普诺夫函数为

对V1求导可得：

式中：kω为转速调节系数。

为使dV1/dt ＜0，选取

式中：Ψsref为参考磁链的平方。

则

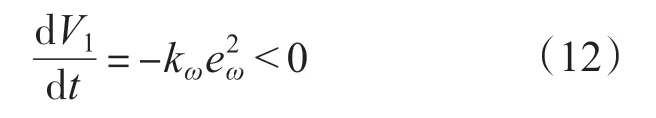
当kω＞0 时，通过李亚普诺夫稳定性分析可知，电机转速可以稳定地跟踪给定转速，转速误差为0。

为控制电磁转矩和磁链，选取转矩误差和磁链误差为状态变量，定义转矩误差和磁链误差分别为

式中：eT为转矩误差；eΨ为磁链误差。

构造新的李亚普诺夫函数

对式（14）求导，可得：

式（15）中包含了系统的实际控制量uα和uβ，为使式（15）满足dV2/dt ＜0，设计实际控制uα，uβ为

式中：kT为转矩调节系数，kT＞0；kΨ为磁链调节系数，kψ＞0。

将式（16）和（17）代入式（15）可得：

则按照式（16）和式（17）控制定子电压可以使得控制系统中的转速收敛，同时可以达到磁链和转矩准确控制的效果，使得系统具有快速的响应速度。

2.2 模糊控制优化反推控制器

针对对反推直接转矩控制系统性能影响较大的2个参数转速调节系数和转矩调节系数设计了模糊控制器，以实现反推控制器参数的在线整定。

选取转矩误差eT和转矩误差的变化率ceT为输入变量，转速调节参数增量Δkω和转矩调节参数的增量ΔkT为输出变量，输入输出变量的隶属度函数如图1所示。

图1 输入输出变量隶属度函数Fig.1 Membership functions of input and output variables

根据kω，kT对系统输出特性的影响，设计Δkω和ΔkT调整原则：当转矩误差偏大时，为快速稳定转矩，选取较大的ΔkT，同时为防止转速有过大超调，选取较小的Δkω；当转矩误差为中等大小时，Δkω和ΔkT取值应适中；当转矩误差值较小时，选取较大的Δkω和较小的ΔkT。所设计的输出Δkω和ΔkT模糊规则表分别见表1和表2。

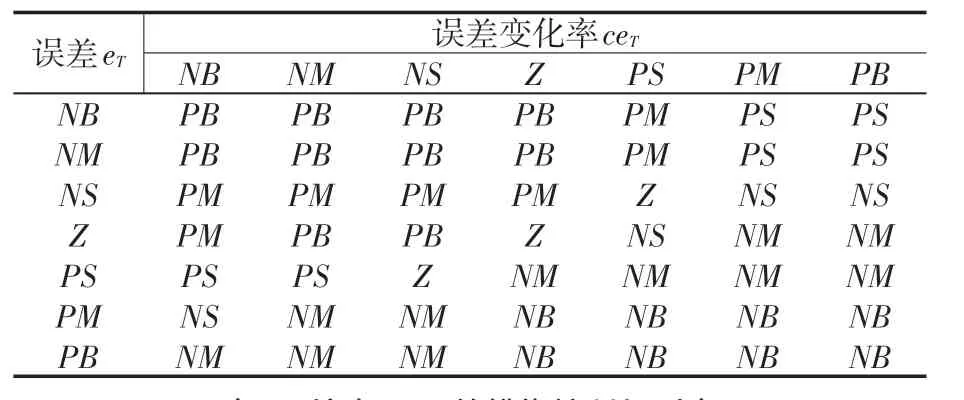
表1 输出Δkω 的模糊控制规则表Tab.1 Table of fuzzy control rules of output Δkω

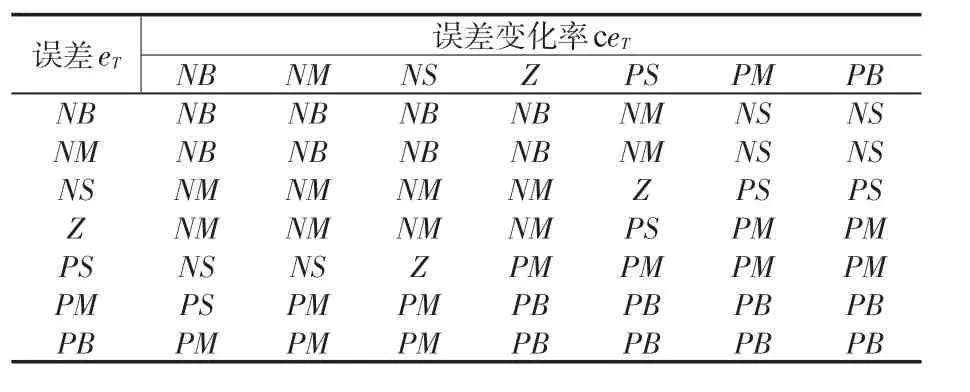
表2 输出ΔkT 的模糊控制规则表Tab.2 Table of fuzzy control rules of output ΔkT

2.3 基于模糊参数优化的反推DTC系统实现

基于模糊参数优化的反推DTC 系统框图如图2所示，与传统直接转矩控制相比，所设计的反推控制器取代了磁链和转矩滞环比较器，模糊控制器利用转矩误差实时调节磁链转矩反推控制器中的转速调节系数kω和转矩调节系数kT。空间矢量调制单元（SVM）取代了传统DTC 中的开关电压矢量表。反推控制器输出定子电压分量uα和uβ，经空间矢量调制单元后产生逆变器开关信号，进而控制永磁同步电机。

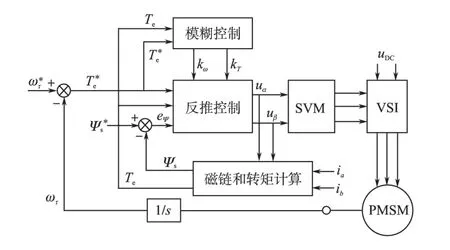
图2 基于模糊参数优化的反推DTC系统框图Fig.2 Block diagram of backstepping DTC based on fuzzy parameters optimization

3 实验分析

为了验证所提出的基于模糊参数优化的永磁同步电机反推DTC 策略，简称改进反推DTC，搭建了一台7.5 kW 的PMSM 调速系统实验样机进行验证分析。实验中永磁同步电机的参数为：永磁体磁链0.24 Wb，d 轴电感8.5 mH，q 轴电感8.5 mH，额定电压200 V，额定电流9.4 A，额定转矩7.15 N·m，定子电阻0.2 Ω，额定转速2 000 r/min，极对数4，转子惯量0.001 23 kg·m2，传统DTC系统的采样频率为10 kHz，磁链滞环宽度为0.001 Wb，转矩滞环宽度为0.02 N·m，反推控制DTC 和基于模糊参数优化的反推DTC 系统均为4 kHz，磁链给定均为0.24 Wb，反推控制DTC 系统中kω=300，kT=1 000，kΨ=7 000。所得到的实验波形如图3～图6所示。

图3 3种控制方法稳态实验波形Fig.3 Experimental results of three strategies at steady-state

图4 3种控制方法启动实验波形Fig.4 Experimental results of three strategies at start-up

图3 是传统DTC、反推DTC和改进反推DTC控制下电机空载运行于600 r/min 时的磁链和转矩稳态实验波形。从图3 可以看出，3 种控制方式下的磁链都稳定运行在给定值0.24 Wb，并且与传统DTC 相比，反推DTC 和改进反推DTC 的磁链和转矩脉动均明显减小。

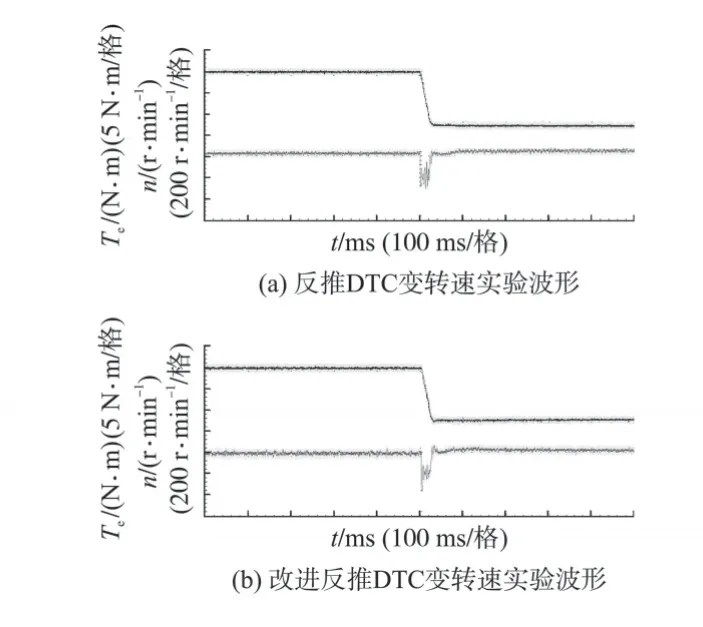
图5 反推DTC和改进反推DTC变转速实验波形Fig.5 Experimental results of backstepping DTC and improved backstepping DTC under step speed

图6 反推DTC和改进反推DTC减载转矩实验波形Fig.6 Experimental results of backstepping DTC and improved backstepping DTC under changed torque

图4 是电机给定转速为1 200 r/min，传统DTC、反推DTC和改进反推DTC控制方式下的电机空载启动时的转速和转矩实验波形。从图4可以看出，当电机启动时，3种控制方法下转速达到给定值的时间均约为0.1 s，具有相同的快速性。

图5是给定转速为800 r/min稳定运行后控制系统参数不变给定转速突变为300 r/min时，反推DTC 和改进反推DTC 控制方式下的电机转速和转矩实验波形。从图5 可以看出，当转速从800 r/min 突减至300 r/min 时，反推DTC 的电机实际转速约为270 r/min，而改进反推DTC的电机实际转速可以稳定在300 r/min。所以由图5可以看出改进反推DTC相比反推DTC具有较强的适应性。

图6 是电机给定转速为500 r/min，负载转矩为3 N·m突减至0 N·m时，反推DTC和改进反推DTC 控制方式下的电机转速和转矩实验波形。从图6可以看出，改进反推DTC具有与反推DTC系统相同迅速的转矩响应。

4 结论

本文提出了一种基于模糊参数优化的永磁同步电机反推直接转矩控制方法，该方法针对直接转矩控制，设计了反推控制器，并针对反推控制器中参数难以确定的问题，采用模糊方法实现了反推控制器中参数的在线调节。实验结果表明基于模糊参数优化的反推直接转矩控制方法在保持传统直接转矩控制系统响应迅速的同时，能够有效减小传统直接转矩控制中的磁链转矩脉动，并具有优良的静动态性能。同时采用模糊控制实现了对反推控制器参数的在线调节，可以大大缩短基于反推控制的改进直接转矩控制系统的调试过程，这对控制系统实现具有重要的意义。

［1］ Zhong L，Rahman M F，Hu W Y，et al.Analysis of Direct Torque Control in Permanent Magnet Synchronous Motor Drives［J］.IEEE Transactions on Power Electronics，1997，12（3）：528-536.

［2］ Casadei D，Serra G，Tani A.Implementation of a Direct Torque Control Algorithm for Induction Motors Based on Discrete Space Vector Modulation［J］.IEEE Transactions on Power Electronics，2000，15（4）：769-777.

［3］ 李耀华，商蓓，刘卫国，等.永磁同步电机直接转矩控制转矩脉动抑制研究［J］.电气传动，2008，38（3）：21-24.

［4］徐艳平，钟彦儒.扇区细分和占空比控制相结合的永磁同步电机直接转矩控制［J］.中国电机工程学报，2009，29（3）：102-108.

［5］Tang Li-xin，Zhong Li-min，Rahman M F，et al.A Novel Direct Controlled Interior Permanent Magnet Synchronous Machine Drive with Low Ripple in Flux and Torque and Fixed Switching Frequency［J］.IEEE Transactions on Power Electronics，2004，19（2）：346-354.

［6］ 杨俊华，吴捷，胡跃明.反步方法原理及在非线性鲁棒控制中的应用［J］.控制与决策，2002，17（S）：641-647.

［7］ Liu Dong-liang，Zhou Li-xin.Application of Backstepping Contro l in PMSM Servo System［C］//ICEMI，2009：3638-3641.

［8］ Rebouh S，Kaddouri A，Abdessemed R，et al.Adaptive Backstepping Speed Control for a Permanent Magnet Synchronous Motor［C］//MASS，2011：1-4.