基于混沌量子蜂群优化SVR的多峰MPPT算法研究

高相铭，杨世凤，潘三博

（1.安阳师范学院物理与电气工程学院，河南 安阳455000；2.天津科技大学自动化学院，天津300222）

光伏发电作为一种最具应用前景的新能源发电技术在近年内得到了飞速发展，但其在应用过程中仍存在发电效率较低的问题。目前，提高光伏系统发电效率的最有效方法之一是采用最大功率点跟踪（MPPT）技术。

光伏阵列在均匀光照情况下的P—V 特性曲线为单峰值，传统的MPPT方法如扰动观测法、电导增量法、恒电压控制法等都能快速而准确地实现最大功率点跟踪［1］。然而在局部阴影的情况下，光伏阵列中各组件的光照度不均匀时，系统的P—V 曲线将呈现多峰值特性，如果仍采用传统的MPPT 方法将很容易使系统陷入局部最大功率点，从而降低发电效率。因此，研究适合于多峰值最大功率点跟踪的光伏MPPT 算法已势在必行。

文献［2-4］对粒子群优化算法应用到多峰值最大功率点跟踪中的问题进行了研究，但是粒子群算法本身容易陷入局部最优，而且算法在运行到后期时粒子趋于同一化，很可能无法找到全局最大功率点。文献［5］将模糊控制与人工神经网络相结合，实现了多峰值最大功率点跟踪，但是该方法中的模糊规则较难确定。文献［6］提出一种基于模糊免疫算法的光伏阵列多峰值最大功率点跟踪方法，但是该算法控制复杂，跟踪精度较差。

基于以上分析可知，多峰值最大功率点跟踪是光伏发电系统中亟待解决的问题。本文提出了一种基于混沌量子蜂群优化SVR 的多峰MPPT 控制算法，该算法将多峰最大功率点跟踪问题当做典型的非线性预测控制问题进行处理。引入SVR 回归模型对局部阴影条件下的光伏阵列最大功率点电压进行回归预测，使光伏阵列工作于全局最大功率点；利用混沌量子蜂群算法的全局优化能力对SVR 的参数进行寻优预处理，保证SVR 回归模型的预测精度和泛化性能；最后通过实验验证了基于混沌量子蜂群优化SVR的多峰MPPT控制算法的有效性。

1 光伏阵列最大功率点多峰特性分析

为了避免局部阴影条件下的热斑效应对光伏组件造成损害，实际运行中的每个光伏组件两端都并联有旁路二极管。当某些光伏组件被阴影遮挡时，旁路二极管导通并流过整个串联阵列的电流，从而保护被阴影遮挡的电池板不受损害。但是旁路二极管导通时，光伏组件或者阵列的输出特性相比均匀光照情况时将发生较大变化。由3个光伏组件串联而成的光伏阵列如图1所示。

图1 并联旁路二极管的光伏阵列电路原理图Fig.1 The circuit model of serial PV module with parallel bypass diode

在均匀光照的情况下，旁路二极管截止，光伏阵列中的每一个光伏组件通过的电流可以用下式描述：

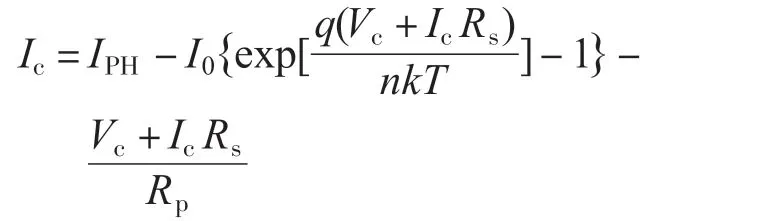
式中：Ic为输出电流；IPH为光生电流；I0为光伏组件的反向饱和电流；q 为电子电荷量，取1.6×10-19；Vc为输出电压；Rs为串联内阻；n 为理想因子；k 为玻尔兹曼常数，取1.38×10-23J/K；T 为电池表面的绝对温度；Rp为并联内阻。

实际光伏电池中，并联内阻Rp的值非常大，因此(Vc+IcRs)/Rp的值同Ic相比非常小，可以忽略不计。上式可以化简为

局部阴影时，光伏阵列中受阴影遮挡的光伏组件的旁路二极管将可能导通，若第i 个光伏组件被遮挡，则其旁路二极管导通时的正向偏压Vb可以描述为

式中：nb为旁路二极管的理想因子；Tb为旁路二极管的温度；I0b为旁路二极管的反向饱和电流；Ic为光伏阵列总输出电流；IPHi为第i个光伏组件被阴影遮挡时的光生电流。

对于图1 所示的光伏阵列，假设3 个光伏组件温度相同，但所受的光照强度各不相同，且光生电流IPH1＞IPH2＞IPH3。随着光伏阵列外接负载电阻由小到大的变化，输出电流Ic逐渐减小，相应光伏组件的旁路二极管将会出现由导通到阻断的变化。根据文献［7］可知，输出电流Ic的大小决定了光伏阵列的输出特性，上述光伏阵列的输出功率可以用分段函数表示。

通过实际的光伏组件搭建上述光伏阵列电路，并在不同的辐照度下对电路进行实际测试，用测试数据对公式中的参数进行拟合，同时根据旁路二极管的性质确定反向饱和电流I0b。最后各参数确定如下：I0=0.022 μA，Rs=0.76 Ω，α=1.043，αb=0.104，I0b=5.95 μA。

光伏阵列数学模型各参数确定后，采用Matlab 软件对两种局部阴影情况下的串联光伏阵列功率输出特性进行仿真，得到的P—V 特性曲线如图2所示。

图2 不同光照情况下光伏阵列的P—V特性曲线Fig.2 P—V characteristic curves under different light levels

实验中的光伏阵列由3个参数一致的光伏组件串联而成，温度都设为25°C。曲线1中的3个光伏组件所受光照情况如下：组件1 为标准光照强度（1 000 W/m2），组件2光照强度为700 W/m2，组件3 为400 W/m2。曲线2 中的3 个光伏组件所受光照情况如下：组件1 为标准光照强度（1 000 W/m2），组件2 光照强度为600 W/m2，组件3 为200 W/m2。

由图2 中的曲线可以看出，当光伏阵列中的各组件所受光照不均匀时，系统的P—V 曲线呈现出多峰特性。

如果仍按照传统的最大功率跟踪策略，可能会使系统陷入局部最大功率点，从而大大降低光伏系统的发电效率。对于曲线1 的情况，如果系统只跟踪到了第1 个局部极值点或第2 个极值点，则其输出功率仅为40 W和70 W左右，距离真正的最大功率点86 W相差了46 W和16 W，将造成输出功率的严重损失。因此，本文提出了一种基于混沌量子蜂群优化SVR 的多峰最大功率点跟踪方法。

2 基于CQABC 优化SVR 的多峰最大功率点跟踪

支持向量回归机（SVR）是一种基于结构风险最小化原则、以统计学习理论为基础的机器学习方法，已经在非线性回归预测控制［8］、数据挖掘等领域得到了成功应用。SVR 中的惩罚系数C、不敏感度系数ε以及核函数参数σ2决定着算法的精度和泛化性能，但是目前对于这3 个参数的选取仍然缺乏有效的解决方案。针对此问题，本文提出了基于混沌量子蜂群算法的SVR 参数优化选择方法，并将优化后的SVR模型用于光伏阵列的多峰最大功率点跟踪，从而提高MPPT 控制的精度。

2.1 量子比特与量子蜂群算法

量子计算以量子力学的相关理论为基础，利用量子所独有的纠缠性、相干性和叠加性达到并行计算的目的，因此具有并行性和指数加速特征，并且表现出了强大的运算能力。相关研究表明，通过将量子计算与传统的智能算法相结合，能够大大提高智能算法的收敛速度和全局优化能力，满足寻优过程中的高性能和高精度的要求［9］。

在量子计算中，量子比特是信息的最小存储单元，它不但能处于“0”和“1”2种状态，还能够处于“0”和“1”之间的任意叠加态。这个叠加态是由“0”和“1”位的线性组合，其大小由概率幅α 和β 决定。通常用Dirac 记号“表示量子态，一个量子比特可以表示为，其中，α,β 表示量子比特在状态“和“的概率，α,β 必须满足：α2+β2=1。

量子空间中，通常采用量子旋转门实现量子比特的状态调整和改变。量子旋转门的数学模型为

量子比特的调整过程为

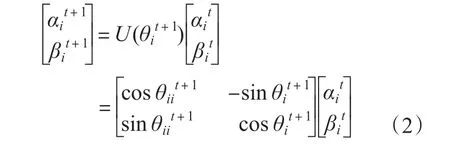
量子蜂群算法（quantum-inspired artificial bee colony，QABC）中，蜜源的位置可以用量子比特来表示，第i个蜜源的量子位置为

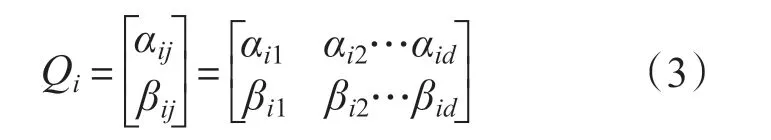
其中

量子蜂群的进化是通过调整量子旋转门从而改变量子比特的状态来实现的，而量子比特的状态代表了蜜源的量子位置，第i 个蜜源量子位置的更新方式如下：

2.2 引入混沌搜索的混沌量子蜂群算法

在量子蜂群算法中，如果某个蜜源的量子位置经过limit 次更新后，适应度值仍无法提高，则表示该蜜源已经陷入局部最优，需要放弃该蜜源，并随机产生新的蜜源来取代它。

本文提出的混沌量子蜂群算法（CQABC）采用了混沌搜索机制来产生新蜜源。该方法利用混沌搜索的随机性和遍历性，以当前陷入局部最优的蜜源位置为基础，通过Logistic 映射迭代产生混沌序列，并提取混沌序列中适应度值最高的解作为新的蜜源位置。通过混沌搜索处理后，陷入局部最优的解得以继续进化，从而提升CQABC算法的收敛速度和精度。混沌搜索的迭代方程如下：

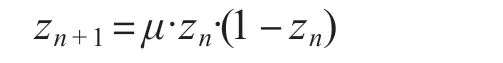
式中：n 为混沌搜索的迭代次数，n=0，1，2，…，d，z0∈（0，1）；μ 为完全混沌搜索μ=4。

该方程迭代运行d 次后将产生一个混沌序列。

假设陷入局部最优的蜜源位置为xk=xk1,xk2,…,xkd,xki∈［ai,bi］，对它进行混沌优化的主要步骤如下：

1）将Xk映射到混沌搜索的迭代方程的定义域［0，1］内，作为混沌搜索的迭代初值，即：

2）用混沌搜索迭代方程进行d 次迭代操作，得到一个混沌序列Zk=(zk1,zk2,…,zkd)。

3）将混沌序列Zk通过逆映射恢复为新蜜源，逆映射公式为

4）重复运行步骤3）L 次，得到L 个适应度值，找出最大的适应度值所对应的作为新蜜源。

本文的CQABC 算法中，除了将混沌搜索用于优化陷入局部极值的蜜源外，还将其用于混沌初始化蜜源种群。

2.3 混沌量子蜂群算法优化选择SVR参数

对于光伏阵列最大功率点预测的SVR模型，CQABC算法需要优化该模型的3个参数C，ε 和σ2，因此被优化问题的解为3 维向量，对应于CQABC 算法中的蜜源位置也是3 维向量。具体的运算步骤如下。

Step 1：初始化量子蜂群参数。设定采蜜蜂、观察蜂以及蜜源的个数为N；算法的最大迭代次数为M；判断蜜源陷入局部最优的阈值参数limit；根据前面介绍的混沌搜索方法初始化蜜源位置并将其变为量子比特的形式。

Step 2：采蜜蜂根据式（4）和式（5）寻找新蜜源的量子位置，并计算新蜜源的适应度值，如果新蜜源的适应度值大于旧蜜源，则用新蜜源的量子位置代替旧蜜源，否则保持旧蜜源的位置不变。

Step 3：观察蜂根据概率公式选择一个质量较好的蜜源，并根据式（4）和式（5）在该蜜源附近寻找到一个新蜜源，通过计算新蜜源的适应度值确定是否保留该蜜源。

Step 4：判断是否有蜜源陷入局部最优，如果有，则该蜜源对应的采蜜蜂变为侦察蜂［10］，并根据前面介绍的混沌搜索方法找到一个新蜜源取代陷入局部最优的蜜源。

Step 5：保存搜索过程中蜜源的最优量子位置（问题的全局最优解）。

Step 6：判断是否达到程序的终止运行条件（通常取决于初始化时设定的最大迭代次数M），如未满足终止条件，返回Step 2继续搜索；否则，输出全局最优位置（SVR 的最优参数值），算法终止。

2.4 基于CQABC-SVR的多峰MPPT算法

基于CQABC-SVR 的光伏系统最大功率点跟踪的实质是一个非线性预测控制问题。系统的输入为各光伏组件的光照度以及温度等环境参数，系统的输出则为上述环境参数下的最大输出功率。支持向量机回归算法以其优异的全局优化能力和泛化性能特别适合于光伏组件的最大功率点进行预测跟踪。

该算法流程如图3所示。其中模型的输入量为温度T 和3 个串联组件各自的光照度S1，S2，S3共4 个变量，输出变量为对应于光伏阵列最大功率点的输出电压值Vmpp。

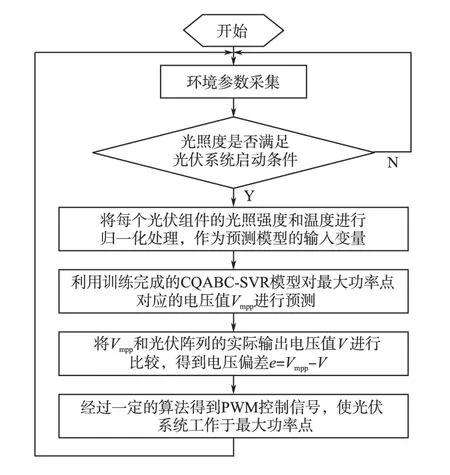
图3 基于CQABC-SVR的多峰MPPT算法流程Fig.3 The flowchart of multi-peak MPPT algorithm based on CQABC-SVR

3 仿真分析

3.1 仿真系统构建

为验证上述CQABC-SVR多峰MPPT算法的有效性，在Matlab/Simulink 环境下建立基于混沌量子蜂群优化SVR 的MPPT 控制系统模型见图4。该系统由几个模块组成：光伏阵列模块、基于混沌量子蜂群优化SVR的最大功率点预测模块、DC/DC模块和PWM驱动电路模块。其中基于混沌量子蜂群优化SVR 的最大功率点预测模块采用m 文件的形式嵌入到Simulink 中。系统输入为各光伏组件的光照强度、组件温度T 和组件的短路电流Isc，输出为SVR模型预测的最大功率点电压Vmpp。系统中的光伏阵列能够仿真光伏组件在各种光照和温度情况下的系统输出特性，实现光照不均条件下的光伏阵列多峰特性的模拟。

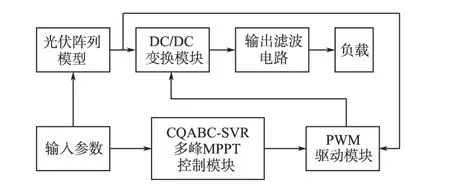
图4 基于CQABC-SVR的多峰MPPT控制系统结构图Fig.4 The structure diagram of multi-peak MPPT controlling system based on CQABC-SVR

3.2 SVR参数的优化选择

为了选择SVR模型的最优参数，需要一定数据作为实验样本进行模型的训练和验证。本文中的样本数据来源于实际的串联光伏阵列实验数据，光伏阵列由3个相同的光伏组件串联而成。通过调整3个组件的不同光照度组合，得到30种不同组合情况下的1 500 组数据。取其中1 200 组数据作为训练数据，300组数据作为验证数据。

采用混沌量子蜂群算法对SVR 模型的参数进行优化选择，算法的参数设置如下：采蜜蜂、观察蜂以及蜜源的个数为50，最大迭代次数为200，阈值参数limit=40。为了比较混沌量子蜂群算法的性能，同时采用交叉验证法和粒子群算法进行SVR参数的寻优实验。结果如表1所示。

表1 不同算法的参数优化结果Tab.1 The results optimized by different algorithms

由表1 可以看出，3 种算法都能寻优得到SVR 的参数，但是3 个参数的结果存在一定的差异。将相应的3个参数赋予SVR模型后，误差指标MSE差别较大：CQABC算法＜PSO算法＜交叉验证方法，运算时间也是CQABC算法最短。

3.3 基于CQABC-SVR的MPPT算法仿真分析

将经过参数寻优的SVR 预测模型以m 函数的形式嵌入到Simulink 的MPPT 控制系统模型中，并设定光伏组件如表2所示。

表2 光伏阵列的相关参数设置Tab.2 The setting parameters of PV arrays

分别采用基于CQABC-SVR的MPPT算法和扰动观察法进行仿真，系统的最大功率跟踪结果如表3 所示。表中本文方法代表基于CQABC-SVR 的MPPT 算法，P&O 方法代表扰动观察法。通过表3中的结果比较可知，本文方法在各种情况下都能跟踪到全局最大功率点，而扰动观察法大多数情况下只能跟踪到局部峰值，而无法跟踪到全局最大功率点。

表3 最大功率点跟踪效果比较Tab.3 The tracking effect of different algorithm

3.4 基于CQABC-SVR 的MPPT 算法在实际环境下性能验证

实际运行中的光伏发电系统所处的环境参数（温度，光照度等）时常发生变化。传统的MPPT算法在环境参数发生突变或者光照度不均匀时将无法实现准确的最大功率点跟踪，而基于CQABC-SVR的MPPT算法能够在任意工况下准确快速地实现最大功率点的跟踪控制。实验所用光伏系统的参数如下：DC/DC 主拓扑电路为Boost 变换电路，开关管选用MOSFET 功率管IRF540N，开关频率为50 kHz。当室外温度为29°C，光照强度由1 000 W/m2突变为600 W/m2时，本文提出的多峰MPPT 算法使系统在0.018 s的时间内稳定于新的最大功率点。而传统的MPPT 算法如扰动观察法虽然也在0.04 s 左右的时间内趋于稳定，但是未能找到全局最大功率点。

图5 为基于CQABC-SVR 的MPPT 算法对实际运行的光伏阵列某一天中的最大功率进行跟踪的曲线。其中在13∶40—14∶20的时间段内，光伏阵列处于不均匀的光照情况下，虽然系统的最大功率点大大降低，但本文提出的算法仍能够对光伏阵列的最大功率点实现准确跟踪。

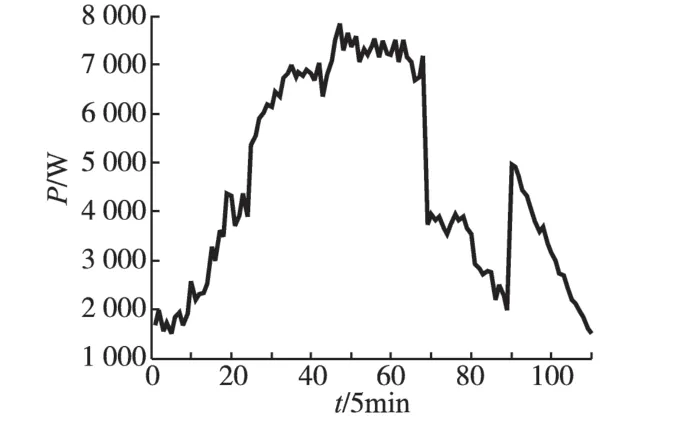
图5 基于CQABC-SVR的MPPT算法在实际环境下的最大功率点跟踪性能Fig.5 The tracking performance of new MPPT algorithm based on CQABC-SVR under physical environment

4 结论

光伏阵列在局部阴影的情况下会导致P—V曲线呈现多峰特性，传统的MPPT 算法很难跟踪到系统的全局最大功率点。针对此问题，本文将支持向量回归机预测模型应用于多峰MPPT控制研究，提出一种基于混沌量子蜂群优化SVR的多峰MPPT控制算法。利用混沌量子蜂群算法的全局优化能力对SVR的参数进行寻优预处理，提高了支持向量回归机模型的预测精度和泛化性能。通过仿真实验和实际数据测试验证了所提算法的有效性。实验结果表明：基于CQABC-SVR的MPPT算法在均匀光照或者局部阴影的情况下均能够准确地跟踪到全局最大功率点，且性能明显优于传统算法（扰动观测法），有效提高了光伏发电系统的输出效率，具有广阔的应用前景。

［1］ 李春玲，石季英，武艳辉，等.模糊控制的扰动观察法在光伏MPPT中的应用［J］.电气传动，2013，43（2）：61-64.

［2］ 朱艳伟，石新春，但扬清，等.粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用［J］.电机工程学报，2012，32（4）：42-48.

［3］ 王雨，胡仁杰.基于粒子群优化和爬山法的MPPT算法［J］.太阳能学报，2014，35（1）：149-153.

［4］ Miyatake M，Veerachary M，Toriumi F.Maximum Power Point Tracking of Multiple Photovoltaic Arrays：a PSO Approach［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）：367-380.

［5］ Bidram A，Davoudi A，S Balog R.Control and Circuit Techniques to Mitigate Partial Shading Effects in Photovoltaic Arrays［J］.IEEE Journal of Photovoltaics，2012，4（2）：2612-2617.

［6］ 刘立群，王志新，张华强.部分遮蔽光伏发电系统模糊免疫控制［J］.电力自动化设备，2010，30（7）：96-99.

［7］ 翟载腾，程晓舫，丁金磊，等.被部分遮挡的串联光伏组件输出特性［J］.中国科学技术大学学报，2009，39（4）：398-402.

［8］ 唐贤伦，李洋，李鹏，等.多智能体粒子群优化的SVR模型预测控制［J］.控制与决策，2014，29（4）：593-598.

［9］ Yao F.Quantum-inspired Particle Swarm Optimization for Power System Operations Considering Wind Power Uncertainty and Carbon Tax in Australia［J］.Industrial Informatics，2012，8（4）：880-888.

［10］高相铭，刘付斌，杨世凤.基于极限学习机的供水管网故障智能诊断方法［J］.计算机工程与设计，2013，34（8）：2887-2891.