基于六参数RC等效电路模型的锂离子电池SOC估计

黄兵锋，杨正才，傅佳宏

(1.湖北汽车工业学院 汽车工程学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002； 2.吉林大学 汽车工程学院 汽车仿真与控制国家重点实验室，吉林 长春 130022； 3.武汉科技大学 信息科学与工程学院，湖北 武汉 430081)



基于六参数RC等效电路模型的锂离子电池SOC估计

黄兵锋1,2，杨正才1，傅佳宏3

(1.湖北汽车工业学院 汽车工程学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002； 2.吉林大学 汽车工程学院 汽车仿真与控制国家重点实验室，吉林 长春 130022； 3.武汉科技大学 信息科学与工程学院，湖北 武汉 430081)

为提高电动车锂离子动力电池荷电状态(SOC)的估算精度，提出了一种基于六参数RC等效电路的电池模型，采用扩展卡尔曼滤波开展对电池SOC的估算方法研究。在考虑未知干扰和环境噪声的影响下，进一步提出了在扩展卡尔曼滤波的基础上的自适应卡尔曼滤波算法，并开展了对电池SOC的在线估算。仿真结果表明：虽然扩展卡尔曼滤波和自适应卡尔曼滤波都对电池SOC有较好的估算精度，但在未知干扰和噪声的影响下自适应卡尔曼滤波具有更好的鲁棒性。

车辆工程；电动车；锂离子电池；荷电状态；自适应卡尔曼滤波

随着电动汽车的快速发展，为其提供能源的动力电池备受关注。为了合理的使用动力电池，减少过充电和过放电带来的风险，并延长电池寿命，理应为电池管理系统(Battery Management System，BMS)提供一个能准确反映电池荷电状态(State of Charge，SOC)的模型。遗憾的是目前还没有哪一类现有的电池模型能够完全准确地反映出电池的各种特性，在这种情况下，对电池各种状态的合理估算就显得极为的重要[1-3]。

笔者主要针对电动车锂离子电池的荷电状态估算进行深入研究。目前，电池SOC估算常用的方法有安时法和开路电压法，近些年一些学者和研究人员提出了模糊逻辑法、神经网络法、卡尔曼滤波法等方法试图对电池SOC进行更加准确的估算，以防止电池过充电(过放电)，延长电池的使用寿命。林成涛等[4]采用改进的安时计量法，提出折算库仑率定义来估算电池SOC；张利等[5]通过构建T-S模型，利用模糊聚类预测法提高SOC估算精度；刘秋丽等[6]提出利用粒子群优化神经网络和阈值方法，提高模型的预测精度；何磊等[7]采用扩展卡尔曼滤波估算SOC，减小了长时间放电引起的累积误差，但没有考虑周围干扰环境噪声的影响。笔者采用扩展卡尔曼滤波对电池SOC进行估算，考虑到外部环境干扰噪声的影响，提出自适应卡尔曼滤波，通过对环境噪声的均值及方差进行在线估算，进一步提高了电池SOC的估算精度。

1 电池等效动力学模型

基于模型的电池SOC估算需要建立一个精确的电池模型，电池的建模通常是将其简化成串联或并联的RC阻容环节[8]，用以模拟动力电池内部快速充放电的反应过程和电池内部缓慢的扩散现象。在诸多电池模型当中，以等效动力学模型应用的最为广泛，而经典的电池模型有分布式等效电池模型、线性等效电池模型、非线性等效电池模型等，其中非线性等效电路模型中以六参数RC电池模型的精度最高，能够较好的反应电池的动态特性。因此，笔者采用六参数RC电池模型作为等效的电池模型[9]，具体的等效电池模型如图1。

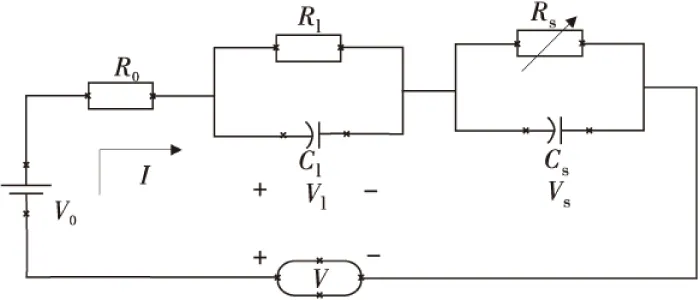
图1 六参数等效RC电池模型Fig.1 Six parameters equivalent RC battery model

图1中：V和I分别为电池的工作电压和工作电流；R0是电池的欧姆内阻；R1，C1用于描述充电时电池双电层部分电压快速上升的动态特性，其两端电压为Vl；Rs，Cs用于模拟放电过程电压缓慢扩散现象，其两端电压为Vs，电压V0用以模拟理想电压源，表征了动力电池储存电能能力的大小，描述了电池的开路电压。

由上述RC等效电池模型，根据电工学中的基尔霍夫电压和电流准则，结合安时计量法建立电池的动力学模型如式(1)～式(5)：

(1)

(2)

(3)

V(t)=V0(t)+Vl(t)+Vs(t)+R0I(t)

(4)

V0(t)=f[S(t)]

(5)

式(1)～式(3)描述了电池模型的内部状态，S(t)代表在t时刻电池的荷电状态；QN是电池的初始容量；f〔S(t)〕描述了动力电池荷电状态SOC与电动势之间的函数关系，它一般情况下是一个非线性函数，可以通过函数拟合来求取。

选取电池的荷电状态SOC、两个RC环电路的电压Vl，Vs作为系统的状态变量，即x=[SOC,Vl,Vs]T。电池的电流I作为系统的输入量，电池的端电压V作为系统的输出量。系统的状态方程如式(6)：

(6)

笔者将在上述锂离子等效模型的基础上对电池SOC进行估算。

2 基于扩展卡尔曼滤波SOC估算

六参数等效RC电池模型是非线性模型，采用扩展卡尔曼滤波进行估算时，首先对系统方程进行泰勒展开，将系统状态空间的非线性部分线性化，然后利用标准卡尔曼滤波算法进行循环迭代，从而对系统的状态变量做算法最优估计。卡尔曼滤波SOC估算具体原理如图2。

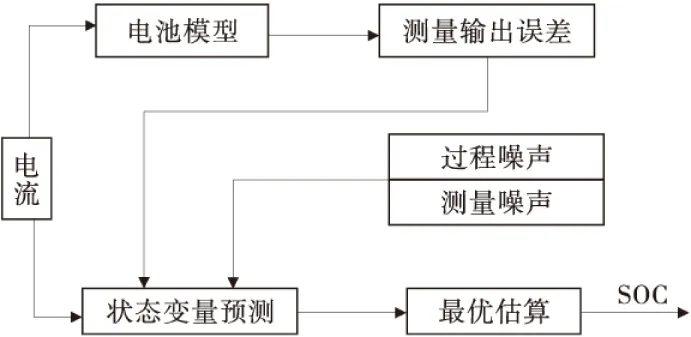
图2 卡尔曼滤波SOC估算原理Fig.2 SOC estimation schematic diagram based on EKF

系统的状态空间模型为式(7)、式(8)：

状态方程

x(k+1)=f[x(k),u(k)]+w(k)

(7)

输出方程

y(k)=g[x(k),u(k)]+v(k)

(8)

式中：f[x(k),u(k)]，g[x(k),u(k)]分别对应非线性状态转移函数和非线性测量函数，图3。

对非线性离散时间状态空间模型进行了描述。

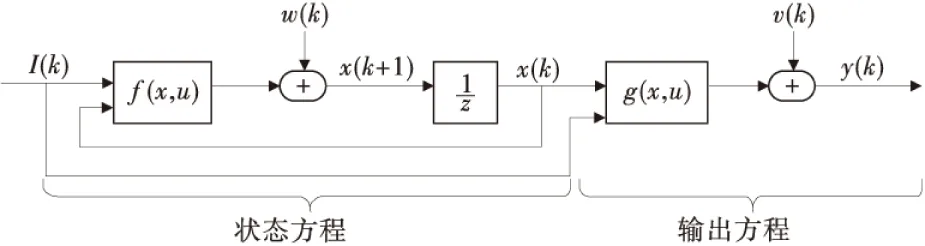
图3 非线性离散时间状态空间模型Fig.3 Nonlinear discrete time state of space model

这里选取的系统状态变量x=[x1x2x3]T=[SOC,Vl,Vs]T，系统的输入为电池的端电流u(k)=I(k)，输出为电池的端电压y(k)=V，w(k)和I(k) 分别为状态空间的过程噪声和测量噪声。

其中

(9)

g[x(k),u(k)]=f[S(t)]+Vl(t)+Vs(t)+R0I(t)

(10)

因此

x(k+1)=Ax(k)+Bu(k)+w(k)

(11)

y(k)=Cx(k)+D(k)+v(k)

(12)

至此，电池模型的非线性部分f[x(k),u(k)]和g[x(k),u(k)]分别由常数项矩阵A，B，C，D来代替，为下面的扩展卡尔曼滤波奠定了基础。其中，

电池模型线性化之后，采用卡尔曼滤波对电池荷电状态SOC进行估计，具体步骤如下[6]。

2.1 系统条件初始化

2.2 系统状态变量和误差协方差预测

状态预测就是根据前(k-1)时刻的状态和误差协方差矩阵来预测k时刻的状态和误差协方差矩阵，公式表示为：

(13)

P(k|k-1)=A(k)P(k-1)AT(k)+Q(k-1)

(14)

2.3 计算卡尔曼增益L(k)

卡尔曼增益根据系统当前状态的估算值对系统状态进行修正，计算公式如式(15)：

L(k)=P(k|k-1)CT(k)[C(k)P(k|k-1)CT(k)+

R(k-1)]-1

(15)

2.4 系统状态变量和误差协方差更新

在预测出系统状态变量和误差协方差之后，卡尔曼滤波会根据卡尔曼增益L(k)和观测变量y(k)对系统状态变量和误差协方差进行更新，以获得更加准确的估算值，具体计算公式如式(16)、式(17)：

1)-D(k)u(k)]

(16)

P(k)=[E-L(k)C(k)]P(k|k-1)

(17)

式(17)中E是单位矩阵，如果P(k)是常数，则E为实数1。

3 基于自适应卡尔曼滤波SOC估算

对于电池SOC估算，在扩展卡尔曼滤波的基础上提出自适应卡尔曼滤波，一方面是在未知干扰环境和噪声的影响下，对电池SOC进行估算的同时，自适应卡尔曼滤波会根据电池的观测数据对噪声的统计特性进行估算；另一方面，卡尔曼滤波在对噪声误差协方差进行估算时，估算的误差有时没有真实地反映出实际误差的变化趋势，从而导致迭代不收敛，估算精度降低。自适应卡尔曼滤波会基于测量数据，根据误差目标值对其进行实时调整，以提高SOC估算精度和干扰环境下的鲁棒性[10]。自适应卡尔曼滤波SOC估算的具体原理如图4。

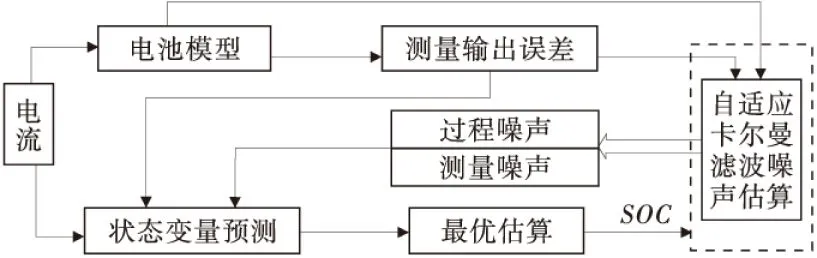
图4 自适应卡尔曼滤波 SOC估算原理Fig.4 SOC estimation schematic diagram based on AEKF

噪声估算模块对过程噪声和测量噪声的均值及协方差进行估算，具体计算如式(18)～式(21)：

(18)

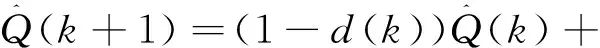
(19)

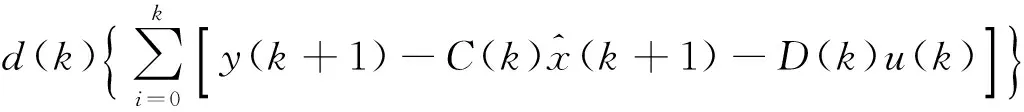
(20)

(21)

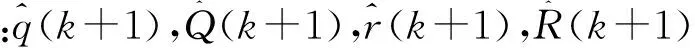
4 仿真结果及分析

在 Simulink 中搭建算法控制策略，电池的额定容量为6 Ah，额定电压为7.2 V，SOC初始值为 0.9，在温度不变的情况下对电池进行恒速驱动工况下的放电试验，放电时间为1 000 s，电池模型参数如表1。

表1 电池模型参数

系统状态的初始值和误差协方差矩阵分别为：

电池的放电电流、电池端电压及SOC估算结果分别如图(5)～图(7)。

图5 电池放电电流 Fig.5 Battery discharge current

图6 电池端电压Fig.6 Battery work voltage

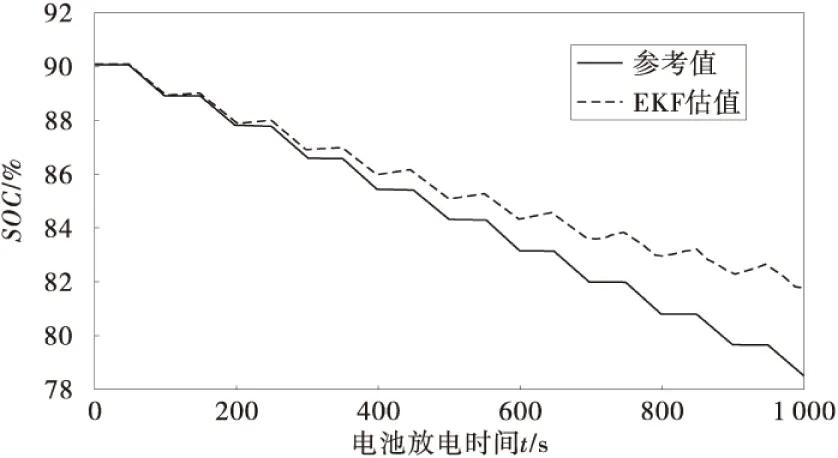
图7 基于EKF算法SOC估计Fig.7 SOC estimation based on EKF algorithm

图8 加入随机噪声的电压Fig.8 Voltage with random noise

从图7可以看出，扩展卡尔曼滤波在电池放电过程的前600 s能够准确地估算出电池的荷电状态，随着放电时间的增加，扩展卡尔曼滤波的估算精度有所降低，这是由于电池的荷电状态受到温度、制造精度等诸多因数的影响造成的。

下面考虑未知干扰和环境噪声对SOC估算的影响，将测量电压加入干扰随机噪声，如图8。电池SOC估算、估算误差及AEKF估算的噪声统计特性分别如图9～图11。

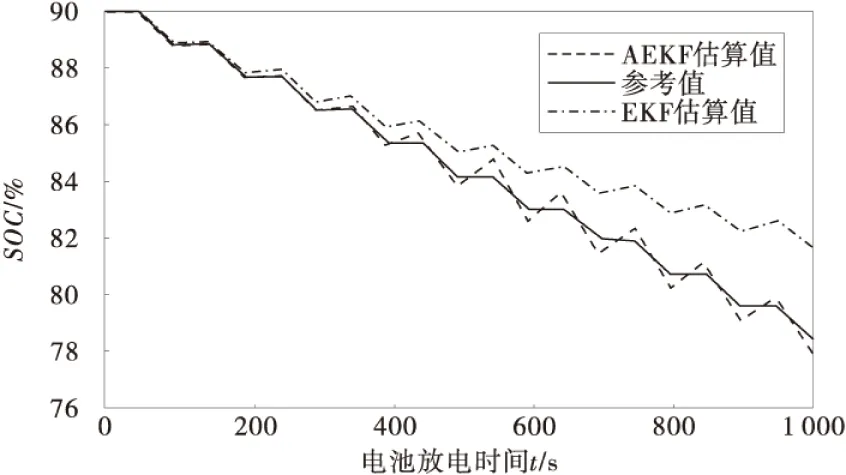
图9 电池 SOC估计Fig.9 Battery SOC estimation

图10 SOC估计误差Fig.10 SOC estimation error

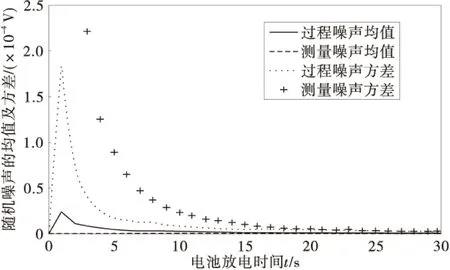
图11 AEKF估算的噪声统计特性Fig.11 Noise statistic characteristics of AEKF estimation

图9的SOC估算结果表明，扩展卡尔曼滤波和自适应卡尔曼滤波都能较准确地估算出电池的SOC。但从整个放电过程来看，随着放电时间的增加，扩展卡尔曼滤波估算精度有所降低，而自适应卡尔曼滤波则自始至终都能很好地估算电池SOC，这是由于自适应卡尔曼滤波在每一次迭代中都会利用测量数据在线估算干扰噪声的均值和方差，并不断修正当前的SOC，从而提高了估算精度和噪声干扰下的鲁棒性。图10的SOC估算误差和图11的AEKF估算的随机噪声统计特性也反映了这一特点。

5 结 语

在建立了六参数等效非线性电路的电池动力学模型的基础上，首先采用了扩展卡尔曼滤波(EKF)迭代算法对SOC进行估算；考虑到电池使用条件的不确定性和环境噪声统计特性的未知性，进一步提出了基于自适应卡尔曼滤波算(AEKF)，通过在线估算未知噪声的统计特性，实时地修正了电池SOC估算值。

仿真结果表明：虽然两种算法均能较为准确地估计电池SOC，但若存在未知外界干扰和环境噪声，则自适应卡尔曼滤波方法的鲁棒性更强。这一结论为进一步进行电池的能量管理、寿命估算等工作奠定了基础。

[1] Chen Min,Rinc’on-Mora,Gabriel A.Accurate.Electrical battery model capable of predicting runtime and I-V performance [J].IEEE Transactions on Energy Conversion,2006,21(4):504-511.

[2] Mo Yuenchow.Online battery modeling and state estimation [EB/OL].[2013-12-13].http://www.adac.ncsu.edu/projects/Battery%20Model/Docs/BatEst3.pdf.

[3] Wang J P,Xu L,Guo J G,et al.Modelling of a battery pack for electric vehicles using a stochastic fuzzy neural network.Proceedings of the Institution of Mechanical Engineers,Part D [J].Journal of Automobile Engineering,2009,223(1):27-35.

[4] 林成涛,陈全世,王军平,等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报：自然科学版,2006,46(2),247-251. Lin Chengtao,Chen Quanshi,Wang Junping,et al.Improved ah counting method for state of charge estimation of electric vehicle batteries [J].Journal of Tsinghua University:Science & Technology,2006,46(2),247-251.

[5] 张利,王为,陈泽坚,等.新能源汽车 SOC估算的模糊预测算法研究[J].电子测量与仪器学报,2011,25(4),315-319. Zhang Li,Wang Wei,Chen Zejian,et al.Research of fuzzy prediction algorithm in SOC estimation of new energy vehicles [J].Journal of Electronic Measurement and Instrument,2011,25(4),315-319.

[6] 刘秋丽,马晓军,袁东,等.粒子群优化神经网络在SOC估算中的应用[J].计算机工程,2012,18(12),143-148. Liu Qiuli,Ma Xiaojun,Yuan Dong,et al.Application of particle swarm optimization neural network in state of charge estimation [J].Computer Engineering,2012,18(12),143-148.

[7] 何磊,宗长富,赵洪辉,等.基于扩展卡尔曼滤波的电动汽车电池状态估计[C]// 2010年第3届电子与智能交通系统国际会议论文集.深圳:[s.n.],2010. He Lei,Zong Changfu,Zhao Honghui,et al.State estimation of power battery in electric vehicle based on extended Kalman filter[C]//Proceedings of 2010 the 3rd International Conference on Power Electronics and Intelligent Transportation System.Shenzhen:[s.n.],2010.

[8] Kutluay K,Cadirci Y,Ozkazanc Y S,et al.A new online state-of-charge estimation and monitoring system for sealed lead-acid batteries in telecommunication power supplies [J].IEEE Transactions on Industrial Electronics,2005,52(5):1315-1327.

[9] U.S.Department of Energy Assistant Secretary for Energy Efficiency,Renewable Energy (RE) Idaho Operation Office.DOE/ID-11069,Freedom CAR Battery Test Manual for Power-Assist Hybrid Electric Vehicles[S].Idaho:Renewable Energy (RE) Idaho Operation Office,2003.

[10] Han Jaehyun,Kim Dongchul,Sunwoo Myoungho.State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter [J].Journal of Power Sources,2009,188(2):606-612.

SOCEstimation of the Electric Vehicle Li-ion Battery Based on Six-Parameter RC Circuit Equivalent Model

Huang Bingfeng1, 2, Yang Zhengcai1, Fu Jiahong3

(1. Hubei Key Laboratory of Automotive Power Train & Electronics, Hubei University of Automotive Technology, Shiyan 442002, Hubei, China; 2. State Key Laboratory of Automotive Simulation & Control, Jilin University, Changchun 130022, Jilin, China;3. School of Information Science & Engineering, Wuhan University of Science & Technology, Wuhan 430081, Hubei, China)

In order to improve the estimation accuracy of state of charge (SOC) for Li-ion battery commonly used in electric vehicles, a battery model was first proposed which was equivalent to a six-parameter RC circuit. The extended Kalman filter (EKF) was then employed to estimate theSOCwhile dealing with the nonlinearity of the battery model. Further to cope with the disturbances caused by unknown and random noises, an adaptive extended Kalman filter (AEKF) algorithm was introduced which estimated the statistical attributes of the noises for the purpose to adaptively adjust theSOCestimation. Simulation results show that the AEKF algorithm is more robust to the external disturbances, although both EKF and AEKF algorithms have quite accurateSOCestimation.

vehicle engineering; electric vehicle; Li-ion battery; state of charge(SOC); adaptive Kalman filter

10.3969/j.issn.1674-0696.2015.05.34

2014-01-02；

2014-03-24

湖北省重点实验室开放基金项目计划(ZDK201206)

黄兵锋(1977—)，男，湖北枝江人，讲师，硕士，主要从事汽车动力学方面的研究。E-mail：ycdt@sohu.com。

U469.71+2

A

1674-0696(2015)05-170-05