盾构隧道洞周土压力颗粒流数值分析

邢心魁, 闫茂龙, 张坤鹏, 李 迎,张 坚

(1. 广西岩土力学与工程重点实验室,广西 桂林 541004; 2. 桂林理工大学 土木与建筑工程学院,广西 桂林 541004)



盾构隧道洞周土压力颗粒流数值分析

邢心魁1, 2, 闫茂龙2, 张坤鹏2, 李 迎2,张 坚2

(1. 广西岩土力学与工程重点实验室,广西 桂林 541004; 2. 桂林理工大学 土木与建筑工程学院,广西 桂林 541004)

对盾构隧道洞周土压力的变化规律进行了数值模拟，研究了不同盾尾空隙、不同直径、不同埋深时隧道洞周土压力的分布规律，分析了隧道正上方土体的应力路径，并对隧道洞周土体竖向位移随埋深的变化规律进行了探讨。结果表明：盾尾空隙小于20 cm时，开挖对竖向土压力的影响区在2.7倍隧道直径范围内，土压力拱主要产生在隧道上部2倍隧道直径范围内；根据隧道正上方不同位置处土体的应力路径，将该区划分为3个区段：① 洞周松动区，② 稳定的压力拱区域，③ 土拱效应不明显的区域；随着隧道埋深的减小，其正上方的地表下沉量逐渐增大，而地表沉降的影响范围逐渐减小。

隧道工程；盾构隧道；土压力；数值分析；盾尾空隙；颗粒流

0 引 言

为解决制约城市发展的交通问题，地铁得到了快速发展。在修建地铁过程中，暗挖法具有不破坏地面交通、建筑物以及地下管线设施等优点，得到广泛应用。盾构法是暗挖法的一种，由于其推进过程中对地表产生的影响相对较小，是目前区间隧道施工的主要方法。盾构隧道的盾尾空隙、管片变形等因素，使洞周土体产生不均匀位移，改变了原始土压力场，对隧道周围建筑物及地下市政设施等产生不利影响[1-2]。因而研究盾构隧道洞周土压力变化规律对提出有效的防治措施有重要指导意义。

笔者基于离散单元法的二维颗粒流程序(PFC2D)，从细观角度研究盾构掘进过程中土压力的变化规律。从前期学者的研究成果来看，PFC2D已用于分析围岩的失稳机制[3-6]。T.Funatsu等[7]和Y.Mitarashi等[8]用PFC模拟了支护对隧道稳定性的影响；A.Fakhimi等[9]用PFC2D模拟了岩石中圆形洞体的开挖问题，分析了洞周围岩的破坏机理；朱伟等[10]已对盾构隧道垂直土压力松动效应进行颗粒流模拟研究；蒋明镜等[11]也已对考虑尾隙的盾构隧道土压力进行了离散元数值分析。

笔者采用PFC2D研究不同盾尾空隙、不同直径、不同埋深时隧道周围土压力的分布规律，分析了隧道上部土体的应力路径，同时对不同埋深条件下隧道周围土体竖向位移的变化规律进行了探讨。

1 盾构隧道PFC2D模型的建立

数值模拟中，围岩参数取自文献[10]。定义下、左、右三道墙体(法向、切向刚度分别为2×108，1.5×108N/m)，创建宽60 m，高80 m的模型箱，在模型箱内随机生成100 000个圆形颗粒(密度为2 630 kg/m3，半径5～10 cm)，颗粒呈均匀分布。确保颗粒间无接触后，对颗粒施加重力加速度，待PFC2D模型达到自重平衡状态后，试样高度被压缩至36.5 m左右。

删除圆形隧道开挖范围内的颗粒，并在衬砌位置处使用FISH函数创建两层颗粒簇(颗粒参数：密度为2 630 kg/m3，内层颗粒半径为9.729 cm，外层颗粒半径根据隧道直径确定，法向、切向刚度分别取7.1×109，3.05×109N/m；平行黏结参数：法向、切向黏结刚度分别取3.55×1010，1.53×1010Pa/m，法向、切向黏结强度均取5.5×106Pa，pb_radius取1)，模拟盾构隧道管片。盾构隧道开挖区域的半径大于管片的半径，二者的空隙即为盾尾空隙(图1)；再次达到自重平衡状态后，可得到隧道洞周土压力的分布规律以及土体位移等。

图1 隧道颗粒流模型Fig.1 Particle flow code model of tunnel

笔者研究内容主要包括：

1)盾尾空隙不同时隧道(半径3 m、埋深23 m)洞周土压力的分布规律，盾尾空隙取5，6，7，8，9，10，11，12，13，14，15，16，18，20，22 cm；

2) 直径不同时隧道(盾尾空隙20 cm、埋深23 m)洞周土压力的分布规律，直径取2，4，6，8，10 m；

3) 埋深不同时隧道(半径3 m、盾尾空隙10 cm)周围土压力的分布规律，埋深取4，6，8，11，14，17，20，23 m。

2 数值模拟结果分析

当盾构隧道开挖且周围土体稳定后，洞周竖向土压力相对竖向自重土压力的变化率等于10%时，则认为该处是隧道开挖对竖向土压力的影响圈边界。对于隧道正上方土压力拱边界的确定，笔者采用了梁晓丹等[12]提出的方法；隧道上方土拱内围岩应力状态与原始自重应力状态相比，最小主应力减小，最大主应力增大，最大主应力的最大值处即为压力拱的内边界；随着至管片距离的增加，外边界根据最小主应力被转移到最大主应力此现象来确定。

2.1 盾构隧道洞周土压力

2.1.1 土压力的分布

图2分别为土体竖向自重应力云图、水平自重应力云图、开挖后竖向应力云图、开挖后水平应力云图(隧道半径3 m、盾尾空隙18 cm、埋深23 m)。

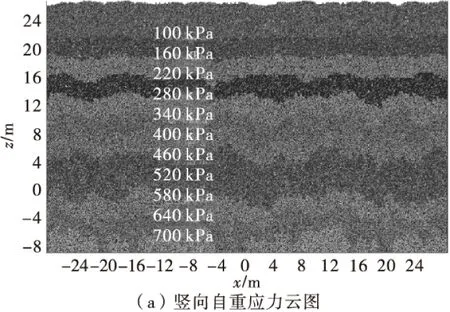
图2 土应力分布Fig.2 Distribution of soil pressure

由图2(a)、(b)可以看出，在自重平衡过程中，不同粒径的颗粒分布不均，使得自重土压力分布横向存在略微的波动，但总体基本符合自重应力分布规律。

由图2(c)、(d)可以看出，由于隧道开挖，洞周土压力产生一定程度的重分布；对于隧道正上方，竖向土压力相对竖向自重土压力显著减小，而水平土压力相对水平自重土压力有先减小后增大的趋势，但最终竖向和水平土压力都趋于自重土压力。

隧道开挖后，由于盾尾空隙的存在，促使围岩向隧道方向产生较大的松胀变形，导致竖向土压力明显减小，近洞壁处土体进入极限状态，水平极限应力较原始土压力降低；随着至管片距离增大，竖向土压力减小幅度降低，而水平土压力逐步增大至极值，而后逐渐回归原位土压力。当至管片的距离超过隧道的影响范围，竖向、水平土压力均趋于初始值。隧道上方土压力的变化规律、竖向土压力的影响圈边界(以下简称为影响圈边界)以及土压力拱的内、外边界(以下简称为内、外边界)如图3。可以看出，影响圈、内、外边界至管片距离分别为12.5，4.6，9.4 m。

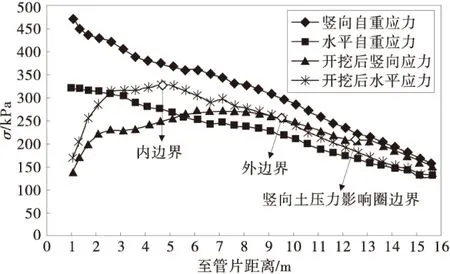
图3 隧道正上方土压应力变化曲线Fig.3 The curve of stress variation just above the tunnel

2.1.2 盾尾空隙对隧道正上方土压力的影响

图4为不同盾尾空隙时隧道正上方影响圈、内、外边界的变化情况。可以看出，盾尾空隙<11 cm时影响圈边界变化不大，当盾尾空隙>11 cm时，随着盾尾空隙的增加影响圈呈线性增大的趋势。这是由于影响圈边界主要受盾尾空隙、管片变形(在土压力作用下管片向两侧变形，上下受到挤压变形)两者的影响，即盾尾空隙或管片变形增加均导致影响圈边界增大；盾尾空隙较小时，管片上的土压力随盾尾空隙的增加而减小[10]，从而导致管片变形也减小，盾尾空隙增加、管片变形减小两因素在一定程度上相互抵消，致使影响圈边界趋于稳定值；盾尾空隙较大时，管片上的土压力不随盾尾空隙的增加而变化，这时可认为影响圈边界只受盾尾空隙的影响，即影响圈边界至管片的距离随盾尾空隙的增加而线性增大。

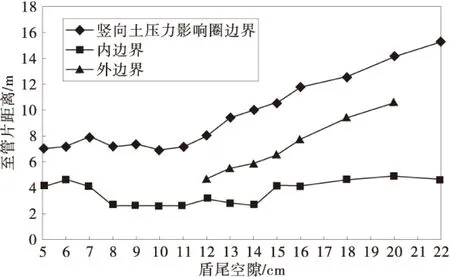
图4 不同盾尾空隙对土压力边界的影响Fig.4 The influence of different shield tail void on earth pressure boundary

内边界至管片的距离在2.6～4.6 m范围内波动，可认为盾构隧道压力拱的内边界至管片的距离在1倍隧道跨度范围内，随盾尾空隙变化不敏感。外边界至管片的距离(外边界不存在的点未标出)随盾尾空隙的增加呈线性增大。

图5为不同盾尾空隙时隧道正上方峰值水平土压应力的变化情况。由图5可知，该峰值应力随盾尾空隙的增加大体呈对数曲线增大。

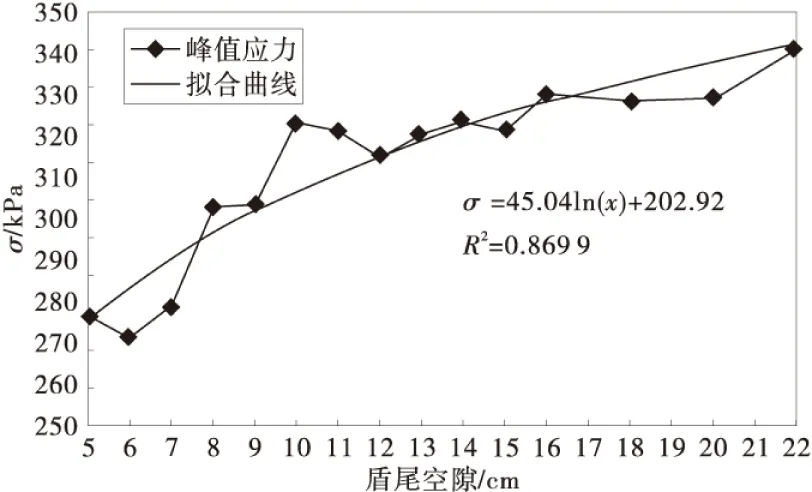
图5 不同盾尾空隙对峰值水平土压应力的影响Fig.5 The influence of different shield tail void on peak horizontal stress

2.1.3 直径对隧道正上方土压力的影响

图6为不同直径时隧道正上方影响圈、外边界的变化情况，d为至管片距离与隧道直径的比值。由图6并结合盾尾空隙对隧道正上方土压力的影响可知，盾尾空隙小于20 cm时，隧道开挖影响圈在2.7倍隧道直径范围内，土压力拱主要分布于2倍隧道直径范围内。

2.1.4 埋深对隧道正上方土压力的影响

图7为不同埋深时隧道正上方影响圈、内边界的变化情况。由图7可知，在埋深<2倍隧道直径时，受埋深的影响内边界、影响圈边界至管片的距离整体上随埋深增加而增大；埋深>2倍隧道直径时，随着埋深的增加，基本保持不变。

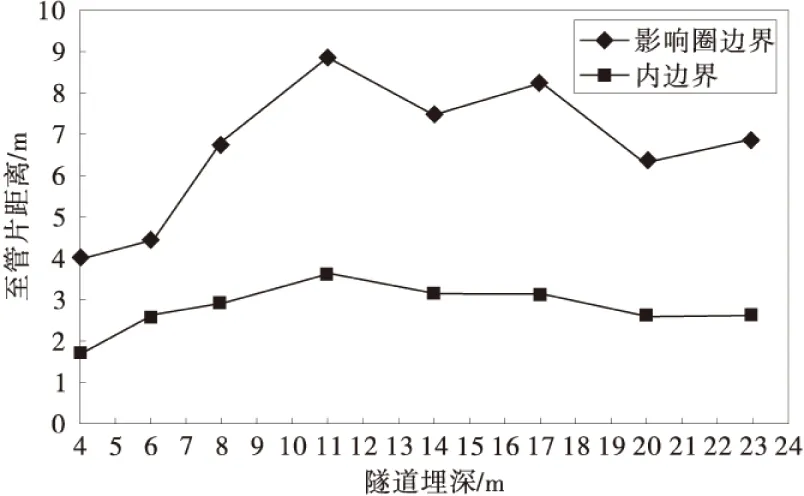
图7 不同埋深对土压力边界的影响Fig.7 The influence of different buried depth on earth pressure boundary

2.2 盾构隧道正上方土体应力路径

图8为隧道正上方不同位置处土体的应力路径(隧道半径3 m、盾尾空隙18 cm、埋深23 m)，σ1为竖向土压力，σ2为水平土压力，平均应力p=(σ1+σ2)/2，偏应力q=(σ1-σ2)/2。由图8可看出，隧道开挖后，距管片1.6 m处的测点，其平均应力、偏应力的绝对值均相对初始值明显减小；距管片4.6 m处的测点，其平均应力相对初始值略有减小，偏应力的绝对值明显减小；距管片14.6 m处的测点，其平均应力和偏应力相对初始值均无显著变化。平均应力与偏应力的大小对土体稳定性有重要影响，据此可将隧道正上方(对土压力产生影响的范围)土体分为三个区：①洞周较松动的区域，该区平均应力、偏应力的绝对值与各自初始值相比都明显减小；②稳定的压力拱区域，该区平均应力与初始值相比略有减小，偏应力的绝对值明显减小；③土拱效应不明显的区域，该区平均应力、偏应力均与各自初始值相比几乎无变化。

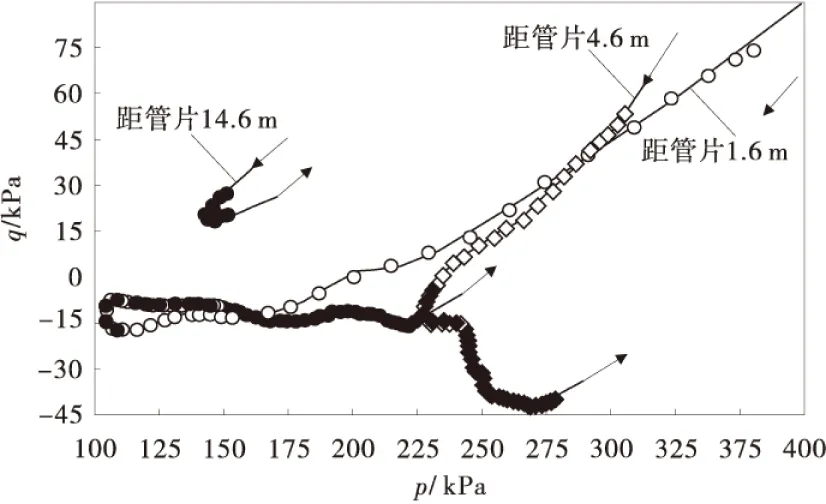
图8 隧道正上方土体应力路径Fig.8 The stress paths of soil just above the tunnel

2.3 盾构隧道洞周土体竖向位移

图9是跨度为6 m、盾尾空隙为10 cm、埋深为23 m时隧道开挖稳定后洞周土体的竖向位移云图。隧道的顶部土体下沉，底部土体向上回弹，这是由开挖卸载所致(与文献[11]所分析的一致)。隧道洞周土体位移较大，位移主要集中于隧道1.5倍跨度范围内。图10为不同埋深时地表横向沉降分布情况。由图10可知，随埋深减小，隧道正上方地表下沉量逐渐增大，但地表沉降的影响范围(下沉量≥3 mm)逐渐减小。

图9 隧道周围土体竖向位移云图(单位：m)

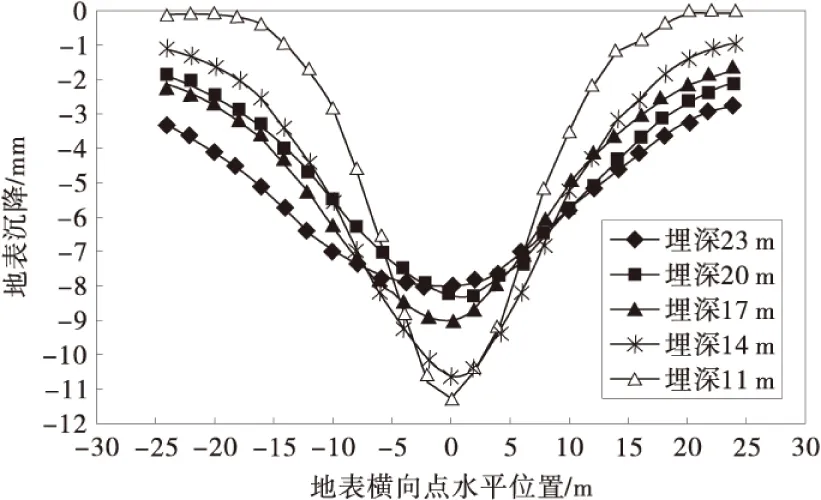
图10 不同埋深条件下地表沉降曲线Fig.10 Curves of ground surface subsidence with different buried depth

3 结 论

笔者采用离散单元法软件模拟了盾尾空隙、直径、埋深对盾构隧道洞周土压力变化规律的影响，分析了隧道正上方土体应力路径和洞周土体竖向位移，得到的主要结论如下：

1)埋深相同的条件下，盾尾空隙<11 cm时，盾构隧道正上方竖向土压力的影响圈边界基本保持不变；盾尾空隙>11 cm时，随着盾尾空隙的增加影响圈边界呈线性增大的趋势；隧道正上方土压力拱的内边界至管片的距离在1倍跨度范围内，基本不随盾尾空隙而变化，外边界至管片的距离随盾尾空隙的增加线性增大；盾尾空隙<20 cm的范围内，对于隧道上部，开挖对竖向土压力的影响区在2.7倍隧道直径范围内，土压力拱主要产生在2倍隧道直径范围内；隧道正上方峰值水平土压应力随盾尾空隙的增加呈对数曲线增大的趋势。

2)盾尾空隙相同的条件下，埋深<2倍隧道直径时，隧道正上方竖向土压力的影响圈边界以及土压力拱的内边界随埋深而变化；埋深>2倍隧道跨度时，随埋深的增加，影响圈边界、内边界均基本保持不变。

3)根据隧道正上方不同位置处土体的应力路径，可将该区分为：①洞周较松动的区域，该区平均应力、偏应力的绝对值均相对于各自初始值明显减小；②稳定的压力拱区域，该区平均应力与初始值基本一致，偏应力明显减小；③土拱效应不明显的区域，该区平均应力、偏应力相对于各自初始值均几乎无变化。

4)盾尾空隙相同的条件下，随埋深的减小，隧道正上方的地表下沉量逐渐增大，但地表沉降的影响范围逐渐减小。

[1] 朱逢斌,杨平,林水仙.盾构隧道施工对邻近承载桩基影响研究[J].岩土力学,2010,31(12):3894-3900. Zhu Fengbin,Yang Ping,Lin Shuixian.Study of influence of shield tunneling on neighboring loaded piles [J].Rock and Soil Mechanics,2010,31(12):3894-3900.

[2] 王正兴,缪林昌,王冉冉,等.砂土隧道施工对下卧管线影响的试验和数值模拟分析[J].岩土工程学报,2014,36(1):182-188. Wang Zhengxing,Miao Linchang,Wang Ranran,et al.Physical model tests and PFC3Dmodeling of soil-pipe interaction in sands during tunneling [J].Chinese Journal of Geotechnical Engineering,2014,36(1):182-188.

[3] 汪成兵,朱合华.隧道塌方影响因素离散元分析[J].地下空间与工程学报,2007,3 (8):1490-1495. Wang Chengbing,Zhu Hehua.Study on the influence factors of tunnel cave-in by the discrete element method [J].Chinese Journal of Underground Space and Engineering,2007,3(8):1490-1495.

[4] 汪成兵,朱合华.隧道塌方机制及其影响因素离散元模拟[J].岩土工程学报,2008,30(3):450-456. Wang Chengbing,Zhu Hehua.Tunnel collapse mechanism and numerical analysis of its influence factors [J].Chinese Journal of Geotechnical Engineering,2008,30(3):450-456.

[5] 王涛.隧洞围岩破坏的颗粒流模拟方法研究[C]//第九届全国岩土力学与工程学术大会论文集.北京:科学出版社,2006:464-471. Wang Tao.Research on simulation of rupture of rock mass of tunnel based on particle flow method [C]// Proceedings of Ninth National Conference on Geomechanics and Engineering.Beijing:Science Press,2006:464-471.

[6] C.Wang,D.D.Tannant.Rock fracture around a highly stressed tunnel and the impact of a thin tunnel liner for ground control [J].Internal Journal of Rock Mechanics & Mining Sciences,2004,41(3):1-8.

[7] Funatst T,Hoshina T,Ishikawa M,et al.Numerical analysis to better understand the mechanism of the effects of ground supports and reinforcements on the stability of tunnels using the distinct element method[C]// ISRM International Symposium 2006,4th Asian Rock Mechanics Symposium.Singapore:World Scientific Publishing Co.Pte Ltd.,2006.

[8] Mitarashi Y,Tezuka H.The evaluation of the effect of long face bolting by 3D distinct element method [C]//ISRM International symposium 2006,4th Asian Rock Mechanics Symposium.Singapore:World Scientific Publishing Co.Pte Ltd.,2006.

[9] Fakhimi A,Carvalho F,Ishida T,et al.Simulation of failure around a circular opening in rock [J].International Journal of Rock Mechanics and Mining Sciences,2002(39):507-515.

[10] 朱伟,钟小春,加瑞.盾构隧道垂直土压力松动效应的颗粒流模拟[J].岩土工程学报,2008,30(5):750-754. Zhu Wei,Zhong Xiaochun,Jia Rui.Simulationon relaxation effect of vertical earth pressure for shield tunnels by particle flow code [J].Chinese Journal of Geotechnical Engineering,2008,30 (5):750-154.

[11] 蒋明镜,王富周,朱合华.考虑尾隙的盾构隧道土压力离散元数值分析[J].地下空间与工程学报,2010,6(1):28-32. Jiang Mingjing,Wang Fuzhou,Zhu Hehua.Numerical simulation on earth pressure for shield tunnels incorporating tail gaps by DEM [J].Chinese Journal of Underground Space and Engineering,2010,6(1):28-32.

[12] 梁晓丹,刘刚,赵坚.地下工程压力拱拱体的确定与成拱分析[J].河海大学学报:自然科学版,2005,33(3):314-317. Liang Xiaodan,Liu Gang,Zhao Jian.Definition and analysis of arching action in underground rock engineering [J].Journal of Hohai University:Natural Science,2005,33(3):314-317.

Particle Flow Code Numerical Analysis on Earth Pressure of Shield Tunnels Cave

Xing Xinkui1, 2, Yan Maolong2, Zhang Kunpeng2, Li Ying2, Zhang Jian2

(1. Guangxi Key Laboratory of Geo-Mechanics & Geo-Technical Engineering, Guilin 541004, Guangxi, China; 2. School of Civil Engineering & Architecture, Guilin University of Science & Technology, Guilin 541004, Guangxi, China)

Lots of numerical simulations were carried out on the change rule of earth pressure around the shield tunnel. The research work was about the distribution of the earth pressure around the tunnel considering the factors of shield tail void, diameter and buried depth. The soil’s stress path just above the tunnel was analyzed, in addition, exploring the change rule of soil’s vertical displacement under the condition of different buried depth around the tunnel. The results show that when the shield tail void is less than 20cm, the affected area of vertical earth pressure from excavation is within the range of soil of 2.7 times the tunnel diameter, and the soil arching mainly takes place within the range of soil of 2 times the tunnel diameter above the tunnel. According to the soil's stress path at different locations of the upper part of the tunnel, the region is divided into three sections, which are relative loose area around the tunnel, the stable pressure arch area and the area of inconspicuous soil arching effect. With the decrease of the embedded depth of the tunnel, the subsidence of the earth’s surface just above the tunnel is increased gradually, but the influence scope of the surface’s subsidence is decreased gradually.

tunnel engineering; shield tunnel; earth pressure; numerical analysis; shield tail void

10.3969/j.issn.1674-0696.2015.05.06

2014-06-30；

2014-09-27

国家自然科学基金项目(51068004)；广西岩土力学与工程重点实验室基金资助项目(11-CX-03)

邢心魁(1964—)，男，河南漯河人，教授，博士，硕士生导师，主要从事岩土工程与地下工程方面的研究。E-mail:597983647@qq.com。

U451

A

1674-0696(2015)05-029-04