基于改进遗传算法的带软时间窗果蔬运输路径选择问题∗
2015-06-09李培庆何黄永升范晨昊高海丹
李培庆何 杰▲黄永升范晨昊高海丹
(1.东南大学交通学院 南京 210096;2.东南大学自动化学院 南京 210096)
基于改进遗传算法的带软时间窗果蔬运输路径选择问题∗
李培庆1何 杰1▲黄永升2范晨昊1高海丹2
(1.东南大学交通学院 南京 210096;2.东南大学自动化学院 南京 210096)
为了研究果蔬在运输过程中受到的振动、冲击和碰撞对产品质量的不利影响,提出了一种包含带软时间窗、路面不平度和道路等级影响等因素的改进遗传算法模型。该模型是以改进目标函数、适应度函数和交叉因子为参数设置,对配送成本进行最小优化分析。将此模型与传统OX交叉遗传算法和组序交叉遗传算法进行了对比,以江苏省13个地级市之间的果蔬配送路径为案例分析。结果表明与其传统算法相比,提出的改进遗传算法能够对成本的预测提高15.3%。
交通管理;果蔬运输;路径选择;软时间窗;遗传算法
0 引 言
果蔬配送与其他工业商品的运输配送路径相比,存在着较强的季节性、地域性、易腐性、易损性和时效性等因素,这给贮藏、运输、销售等物流环节带来了较多的困难。除了果蔬易腐性和时效性外还具有较强的易损性,因为在运输过程中的果蔬极易受到外界振动、冲击、碰撞等,特别是粗糙的路面不平度和低等级道路很容易导致果蔬碰撞受损。此外,考虑到客户对于产品的接收是一个软时间窗,即过早运达,会造成因不能及时销售的仓储成本,过晚运达会造成销售的不及时,以及果蔬的腐坏[1-4]。
针对配送车辆路径(VRP)配送优化问题,国内外学者进行了诸多方法的研究和探讨。文献[1]以易腐货物配送中时变车辆路径问题为研究对象,提出以集成遗传算法为优化手段,用于搜索行驶路线问题的最优解。文献[2]针对果蔬运输中遇到无法按时送达配送点的特殊情况,通过蚁群算法对其他运输车进行路径再规划,得出带时间窗的再规划数学模型。文献[3]采用并行遗传算法作为易腐物品的车辆路径问题的改进措施,通过设计交叉和变异算子,提高了算法的计算效率和性能。文献[4]借助于RFID,GPS,GRS等现代科学技术,分析了在物联网运输线路调度系统下,解决生鲜产品在冷链物流配送下运输路径优化问题,证明了基于物联网的运输线路调度系统是可行的。文献[5]为了快速高效地找出最优的联运路径,建立了带有时间窗约束的多目标、多运输方式、多货种的Martins算法路径选择改进模型,进而缩小了解空间和避免了生成无效路径。文献[6]建立了以路径税收政策为强化学习导向的危化品运输路径选择的演化博弈模型,对降低危化品运输风险具有实际意义。文献[7]采用动态线性标定方式,对遗传算法中的交叉算子采用大变异操作设计,建立和优化了车辆路径问题的数学模型,得出较为满意结果。文献[8-9]分析了具有易腐性的新鲜蔬菜配送特点,提出了基于禁忌搜索的启发式算法求解策略,显著地提高了易腐产品的配送效率。文献[10-11]针对高度易腐食品和持续性食品供应链为研究对象,以多目标规划模型为理论,通过进化算法权衡了配送成本情况与新鲜度之间的关系。文献[12-13]主要对易腐性食品和农产品供应链的配送方法进行了回顾和总结。
上述文献采用了多类算法对运输路径进行了优化分析,这为进一步研究特定条件下果蔬运输路径优化问题提供了理论基础。由于果蔬具有含水量高、保鲜期短、销售和消费都存在很强的时效性特点,而且在运输过程中极易受到路面不平度和低等级道路产生的振动与冲击对其易损性的影响,以及选取不同运输路径时道路等级收费标准的影响,因此,要用科学的方法确定合理的果蔬车辆配送路线,然而产品过包装又会增加运输成本。为了解决这一类果蔬配送路径与成本优化问题,将针对果蔬的运输特性,即易损性、易腐性和时效性等因素,并考虑配送中的带软时间窗、运输路面不平度对果蔬质量造成的影响及公路收费等级差异性等因素,构建了适合果蔬运输的改进遗传算法的数值模型。将此模型与原始OX交叉遗传算法和组序交叉遗传算法进行了对比,以江苏省13个地级市之间的果蔬配送路径为案例分析,说明了改进后算法的有效性和可行性。
1 数学模型构建
提出了一个带有路面不平度等级系数,以及不同道路收费等级的数学模型,在这个模型里供应商要确定每个零售商所需的配送需求量,以及配送时的路径选择。配送的目标就是怎样使在一次完整的配送之后所需成本最少。假设配送中心有m个同一类型的车辆,给分布在区域内的不同的n个客户配送货物,每辆车的最大运输容量和运行距离分别用L和Q表示。因此,基于总的最少成本的目标函数C可以用公式表示为
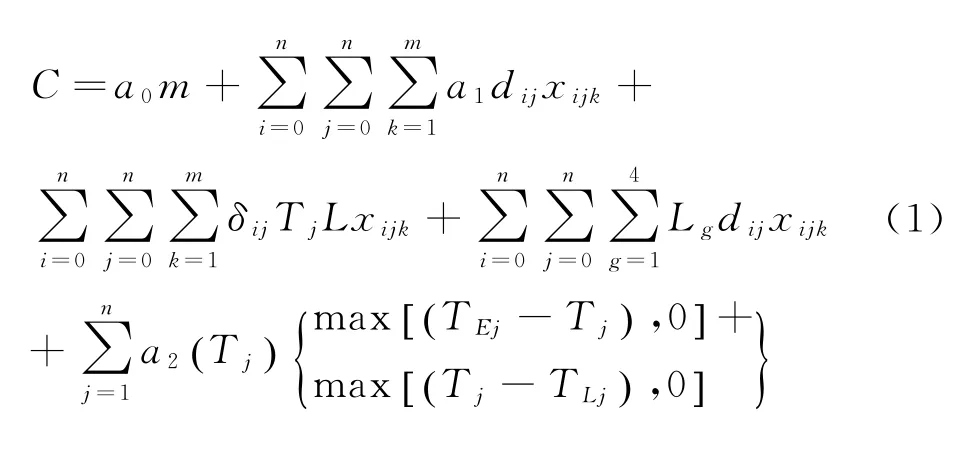

式中:qi为客户i的果蔬需求量;δij为客户i至客户j之间道路路面不平度等级系数,取值见表1[14-15]; dij为客户i与客户j 2地点距离;[TEj,TLj]为第j个客户的接收时间窗;Tj为车辆从配送中心运行至第j个客户地点的时间,L为不同g公路等级的每公里收费成本[16];m为配送车辆总数;n为配送客户总数;Q为每辆车的最大容量;L为每辆车的最大行驶距离。

表1 道路路面不平度等级系数Tab.1 Road level and roughness evaluation coefficient万人·km/d
式(1)中,第1项为m辆果蔬运输车辆的固定成本,第2、3项为运输车辆行驶消耗成本,第4项为由于路面不平度对果蔬振动与冲击产生的损耗成本,第5项为运输车辆超出客户要求时间窗时支付的惩罚成本,目标函数是使4项之和,即总成本最小。其约束条件为

式(3)说明所有车辆均从配送中心出发,完成配送后返回配送中心;式(4)保证每辆车的载重量不能大于其最大载重量;式(5)保证每个客户仅由一辆车配送;式(6)保证每辆车的行驶距离不能大于其最大行驶距离;式(7)和(8)为客户时间窗要求,当运输能在时间窗内送达,则可以由该车进行配送。
2 改进遗传算法
2.1 遗传算法
遗传算法相比较于传统的算法,遗传算法从串集开始搜索,覆盖面更大,利于从全局考虑选择最优方案,具有良好的并行性,能够同时处理多个个体,即同时评估搜索空间中的多个解,减少了陷入局部最优解的风险。遗传算法具有自组织、自适应和自学习性。在车辆路径选择问题上,遗传算法显示出了其特有的优势。随着求解规模扩大,精确算法的复杂程度和求解时间都大大增加。遗传算法是一种具有较强鲁棒性的优化算法,拥有良好的全局搜索能力和并行性,适合解决此类运输路径优化问题。
2.2 改进遗传算法设计
2.2.1 染色体编码方式
采用整数编码方式,假设由m辆车完成k个客户的配送任务,则构造1条长度为k+m+1的染色体,其编码形式如:(0,i1,i2,…,ik,0,il,…, im,0)。式中:0为配送中心,ik为客户。其意义解释如下:第1辆车从配送中心出发,经过i1,i2,…,ik这些客户后回到配送中心;第2辆车从配送中心出发后,经过i1,i2,…,im客户后回到配送中心……,k辆车1次出发,完成所有的运输任务,就构成了k条子路径。这样编码的优点在于直观地给出了子路径及客户顺序。
如染色体编码为0630189025740,表示由3辆车完成9个客户的配送任务。
车辆1的路线。配送中心(0)→客户6→客户3→配送中心。车辆2的路线:配送中心(0)→客户1→客户8→客户9→配送中心。车辆3的路线:配送中心(0)→客户2→客户5→客户7→客户4→配送中心。
2.2.2 适应度函数
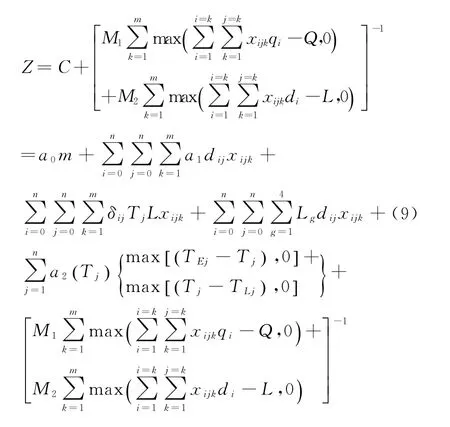
考虑到计算中会出现不可行解,对这些不可行解的处理可以通过引入惩罚策略。定义适应度函数Z为式中:C为目标函数;M1为当一辆车的实际货运量超过其最大承载量Q时的惩罚因子,M2为当一辆车的实际行驶距离超过其最大行驶距离L时的惩罚因子,M1和M2是2个大的正数。
2.2.3 产生初始种群
采用搜索启发式方算法sweep方法将客户分成m组,每组满足所给出的约束条件,在每组的第一个元素前和最后一组的后面各加一个0,则组成了一个染色体编码。例如,将9个客户分成了3组:(6,8,1),(2,9,7),(4,5,3),则染色体编码为0681029704530。如此可产生初始种群。
2.2.4 判断停止条件
判断迭代的代数是否为预设的N,若是,则停止进化,选出当前性能最好的染。
2.2.5 自然选择
采用精英和比例结合的选择策略,将每代x个染色体中的最优染色体复制一个直接进入到下一代,下一代种群中剩下的x-1染色体采用轮盘赌选择法产生。
2.2.6 染色体交叉重组
笔者在基于组序交叉的基础上提出了一种改进的多种群的交叉方式。假设随机选取2父体A和B,将A和B中的各组分别求交,得到一个称为子体核心的部分,这样保证了子体继承父体中一些元素的相对位置,也可使各回路达到一定的均衡且不会出现总路程太长的情况。对于剩余的基因来说,利用贪婪法则将其相继插到离其最近的基因之前,构成子体A’,而对于子体B’的形成,则将剩余的基因按照相反的顺序插入到离其最近距离的基因之后,从而形成子体B’。
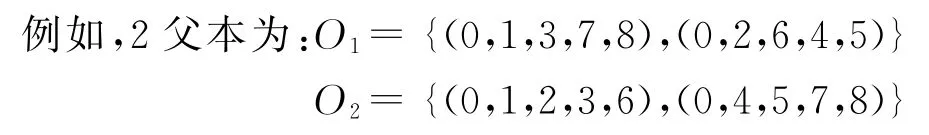
那么染色体O1的第1组、第2组与染色体O2第1组、第2组分别求交后得O1∩O2的核心为O={(0,1,3),(0,4,5)},待定的元素由2,6, 7,8组成。首先构成子体A’:按照2→6→7→8的顺序依次插入O中。假如O中第1组离2最近的点为1距离是5,而第2组离2最近的点为4距离8,则将2放人第1组1之后,检查是否满足约束条件。其它元素处理的方法一样,只是如果一个元素加人使得不满足约束,则将它归入另一组中,而对于子体B’的构成,则按照8→7→6→2的顺序依次插入。
上述交叉方式虽然保证了核心元素的相对位置不变以及种群的多样性,但却对子串有着很大的破坏。为此,引入常用的类OX法与之结合,类OX法可以将交配区完整保留。并且将染色体群分成两部分,一部分用上面的方法交叉,另一部分用OX法交叉,每过一定的代数就交换其中的一部分。
2.2.7 染色体变异
这里选区逆转变异与对换变异相结合的方式,2种变异隔代交替出现。
逆转变异。选取染色体的一个子串,将其翻转。例如,选取了092||0157||038640中的157,则变异后的染色体为0920751038640。
对换变异。随即选取2个染色体上的不为0的基因将其交换位置。例如,0920157038640,选取了9和3交换位置,则形成了子代0320157098640。
3 案例分析
芒果具有营养价值高,产地主要集中我国华南地区,而且芒果在运输过程中很容易受到振动与冲击的影响。假设有一批从华南运来的芒果,需经以南京为配送中心向江苏其他12个地级市进行配送,每辆车限载重12 t,车辆正常行驶里程不超过600 km,假设时间窗惩罚因子α=3 000,β=4 000,超载罚值为M1=6 000,超过行驶上限距离罚值为M2=3 000,对城市之间距离采取简化处理并分为不同的道路等级。表2为各个城市之间的距离,表3为各个城市之间道路等级,实际上城市之间的道路等级至少是2种以上,为了便于计算,本文只列出了案例分析中配送车辆途径线路等级。表4为各个城市需求量及时间窗要求。

表2 各城市之间距离DTab.2 Distance among different cities km

表3 各城市之间道路等级LgTab.3 Road level among different cities Lg
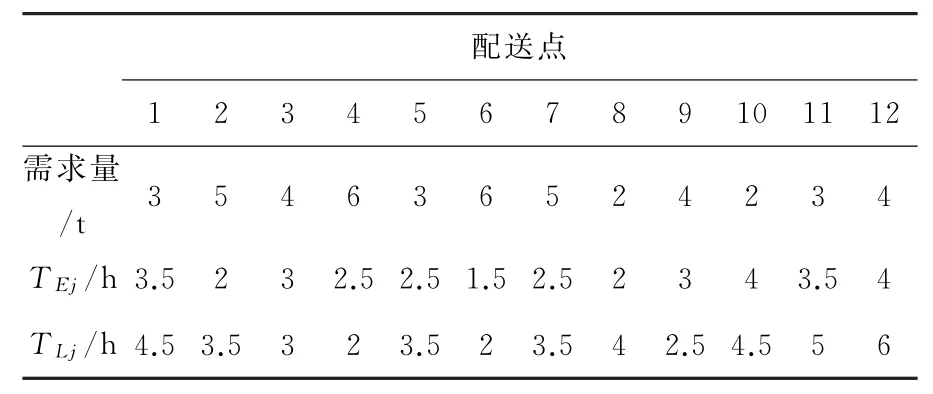
表4 各城市需求量及时间窗要求Tab.4 Demand among cities and time window requests
为了验证改进遗传算法的可行性,将改进的遗传算法和原始OX交叉遗传算法及组序交叉遗传算法进行了对比分析。在Matlab中对这3种算法进行了编程和仿真,相关参数设置为配送车辆4辆,变量维数为30,遗传代数为200,交叉率为0.8,变异率为0.2。图1和图2为3种算法目标值的对比图示。
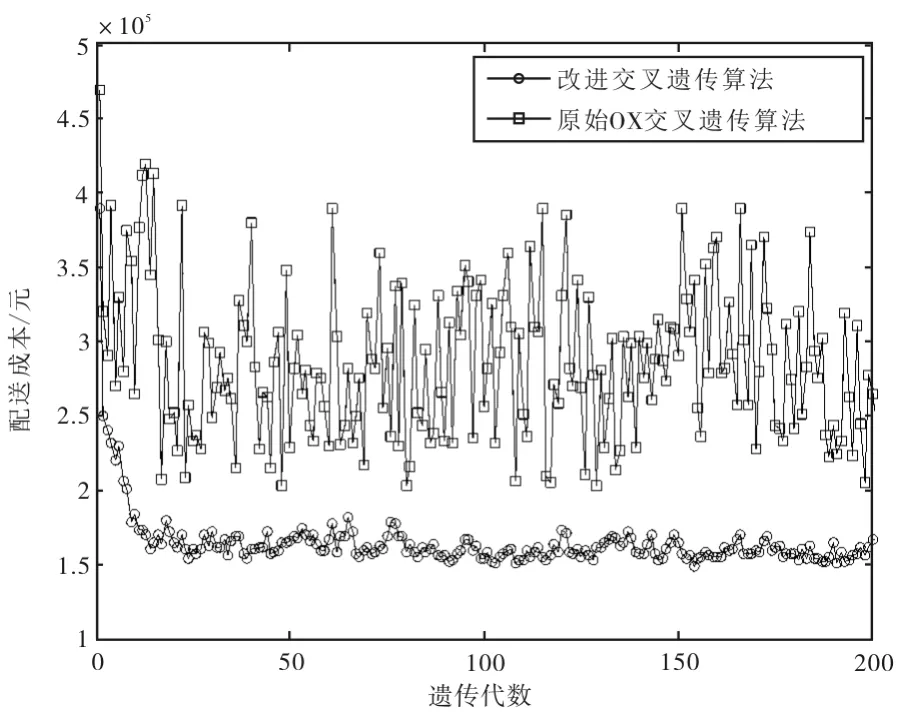
图1 改进交叉遗传算法和原始OX交叉遗传算法对比图Fig.1 Comparison chart between improved genetic algorithm and original OX crossover genetic algorithm
由图1和图2可见,改进交叉遗传算法相比原始OX交叉遗传算法与组序交叉遗传算法,具有收敛速度快,算法能力强等优点,其可靠性优于后两者。通过对改进交叉遗传算法进行了多次试验,可以得到的最后优化结果为0→8→10→12→0→1→7→5→0→4→6→9→0→11→3→2→0,费用值为156 370元,其中,0为配送中心。

图2 改进交叉遗传算法和组序交叉遗传算法对比图Fig.2 Comparison chart between improved genetic algorithm and group-order crossover genetic algorithm
为了进一步研究本文提出的改进遗传算法模型与原始OX交叉法和组序交叉法的对比分析以及改进遗传算法中路面不平度系数和公路收费等级对分析结果的相关性程度,将根据均方根误差(RMSE)、绝对误差(Eabs)和相关系数(Rcor)对其进行评估分析,见式(10)~(12)。

通过对均方根误差、绝对误差、相关系数和运行时间的分析比较可以得出以下结果:①3种算法的精确度从高到低依次为本文提出的改进遗传算法、组序交叉遗传算法和原始OX交叉遗传算法;②从相关系数的改进可以看出,将运输时的路面不平度系数对果蔬质量造成的振动与冲击影响和公路等级及收费差异性因素考虑到改进模型算法中,可以有效地提高运输成本预测精度。总之,通过改进目标函数、适应度函数和交叉因子,构建的改进遗传算法的果蔬本预测模型是可行的和有效的,能够减少果蔬碰撞损失和降低运输成本。
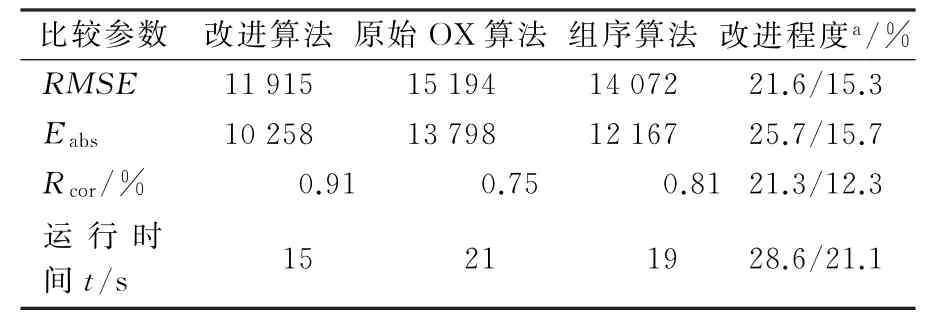
表5 3种算法的比较Tab.5 Comparative analyses between the 3 algorithms
4 结束语
依据提出改进算法分析,解决物流配送中的路径选择问题时,原始OX交叉遗传算法不容易快速收敛到满意值,而采用组序交叉法和原始OX交叉法相结合的改进交叉遗传算法,其组序交叉可以保证核心元素的相对位置不变以及种群的多样性,而OX法可以使交配区完整保留,二者结合,通过改进目标函数、适应度函数和交叉因子,算法能力和优越性得到了显著改善。考虑路面不平度系数对果蔬质量造成的振动与冲击影响和公路等级及收费差异性因素到改进模型算法中,从实验结果中可以看出,构建的改进遗传算法的果蔬预测模型是可行的和有效的,能够减少果蔬碰撞损失和降低运输成本。笔者主要针对同类果蔬的配送问题进行了相关的研究,对于多种果蔬的联合运输最优路径规划是否能取得满意的结果有待进一步的研究。
[1] 李锋,魏莹.易腐货物配送中时变车辆路径问题的优化算法[J].系统工程学报,2010,25(4):492-498.
LI Feng,WEI Ying.Time-dependent vehicle routing algorithm for perishable goods delivery[J].Journal of Systems Engineering,2010,25(4):492-498.(in Chinese)
[2] 黄华芳,王以忠,李达,等.果蔬运输车辆路径再规划[J].农业机械学报,2012(4):113-118.
HUANG Huafang,WANG Yizhong,LI Da,et al.Vehicle route replanning for fruit and vegetable delivery[J].Transactions of the Chinese Society of Agricultural Machinery,2012(4):113-118.(in Chinese)
[3] 谢小良,符卓,杨光华.易腐物品车辆路径问题的并行遗传算法[J].计算机工程与科学,2009,31 (9):64-67.
XIE Xiaoliang,FU Zhuo,YANG Guanghua.A parallel genetic algorithm for the vehicle routing problem of perishable items[J].Computer Engineering &Science,2009,31(9):64-67.(in Chinese)
[4] 刘文佳,李芳.基于物联网的生鲜产品运输路径优化[J].物流工程与管理,2015,37(1):92-94.
LIU Wenjia,LI Fang.Fresh products’distribution path optimization based on the internet of things [J].Logistics Engineering and Management,2015, 37(1):92-94.(in Chinese)
[5] 林枫.基于Martins算法的联合运输最优路径规划[J].西南交通大学学报,2015,50(3):543-549.
LIN Feng.Optimal intermodal transport path planning based on martins algorithm[J].Journal of Southwest Jiaotong University,2015,50(3):543-549.(in Chinese)
[6] 吴军,王丹,李健,等.基于强化学习的危化品运输路径选择博弈分析[J].系统工程理论实践, 2015,35(2):388-393.(in Chinese)
WU Jun,WANG Dan,LI Jian,et al.Game analysis of hazardous chemicals transport route selection based on reinforcement learning-model[J].Systems Engineering—Theory and Practice,2015,35(2): 388-393.(in Chinese)
[7] 张华庆,张喜.改进遗传算法在车辆路径问题中的应用[J].交通信息与安全,2012,30(5):81-86.
ZHANG Huaqing,ZHANG Xi.Application of improved genetic algorithm in vehicle routing problem [J].Journal of Transport Information and Safety 2012,30(5):81-86.(in Chinese)
[8] OSVALD A,STIRN L Z.A vehicle routing algorithm for the distribution of fresh vegetables and similar perishable food[J].Journal of Food Engineering,2008,85(2):285-295.
[9] CHEN H K,HSUEH C F,CHANG M S.Production scheduling and vehicle routing with time windows for perishable food products[J].Computers &Operations Research,2009,36(7):2311-2319.
[10] AMORIM P,ALMADA-LOBO B.The impact of food perishability issues in the vehicle routing problem[J].Computers&Industrial Engineering,2014(67):223-233.
[11] VALIDI S,BHATTACHARYA A,BYRNE P J.A case analysis of a sustainable food supply chain distribution system—A multi-objective approach [J].International Journal of Production Economics,2014(152):71-87.
[12] HSU C I,HUNG S F,LI H C.Vehicle routing problem with time-windows for perishable food delivery[J].Journal of Food Engineering,2007,80 (2):465-475.
[13] AHUMADA O,VILLALOBOS J R.Application of planning models in the agri-food supply chain: A review[J].European Journal of Operational Research,2009,196(1):1-20.
[14] JTG B01-2014,公路工程技术标准[S].北京:人民交通出版社,2014.JTG B01-2014,Technical standard of highway engineering[S].Beijing:People Communication Press,2014.(in Chinese)
[15] LIN J H.Variations in dynamic vehicle load on road pavement[J].International Journal of Pavement Engineering,2014,15(6):558-563.
[16] 江苏省交通运输厅.江苏高速公路收费费率标准[S].南京:江苏省交通运输厅,2013.
Jiangsu Provincial Communication Department.Jiangsu expressway toll rate standard[S].Nangjing:Jiangsu Provincial Communication Department,2013.(in Chinese)
Fruit and Vegetable Distribution with Soft Time Windows Based on an Improved Genetic Algorithm
LI Peiqing1HE Jie1▲HUANG Yongsheng2FAN Chenhao1GAO Haidan2
(1.School of Transportation,Southeast University,Nanjing 210096,China; 2.School of Automation,Southeast University,Nanjing 210096,China)
In order to investigate the impacts of vibration,shock and collision on fresh fruits and vegetables during transportation,an improved genetic algorithm model is developed based on the soft time windows,pavement roughness and road grades.The objective of this model is to minimize the delivery costs of the suppliers by improving objective function,fitness function and crossover operator.Furthermore,comparison analyses are conducted among improved genetic algorithm,original order crossover(OX)genetic algorithm and group-order crossover genetic algorithm with a focus on the transport routes of fresh fruits and vegetables among 13 cities in the Jiangsu province as a case study.The results indicate that the proposed model provide 15.3%higher accuracy of delivery cost estimation over the conventional models.
transportation management;fruits and vegetables transport;distribution;soft time windows;genetic algorithm
U491
A
10.3963/j.issn 1674-4861.2015.05.005
2013-10-12
2015-09-18
∗国家自然科学基金项目(批准号:51078087)、中央高校基本科研业务费专项资金项目(批准号:CXLX12_0111)、2015年度河南省重点科技攻关项目(批准号:152102310255)、江苏省高校“青蓝工程”中青年学术带头人培养对象项目(批准号:2014)、浙江省交通运输厅科技计划项目(批准号:2012H12)资助
李培庆(1986-),博士研究生.研究方向:交通运输安全与物流路径优.E-mail:lpqing@163.com
▲通信作者:何 杰(1973-),博士,教授.研究方向:交通安全与评价.E-mail:hejie@seu.edu.cn
