线激光路面车辙仪测量不确定度评定*
2015-06-09荆根强王义旭郭鸿博
荆根强 王义旭 郭鸿博
(交通运输部公路科学研究所,北京 100088)
线激光路面车辙仪测量不确定度评定*
荆根强 王义旭 郭鸿博
(交通运输部公路科学研究所,北京 100088)
线激光路面车辙仪的横断面测量具有连续性,通过算法分析总能得到车辙断面关键点处的高程。因此,其测量不确定度主要来源于高程测量模型建立时的线性拟合过程。本文从测量原理入手,阐述了高程计算模型的推导过程,并采用实例说明了线激光路面车辙仪测量不确定的评定方法。
计量学;道路检测;线激光车辙仪;不确定度
0 引言
线激光路面车辙仪是目前我国普遍使用的一种快速路面车辙测量仪。它采用连续线结构激光及数字成像装置,通过图像分析及三角测量技术获取车辙横断面信息[1],用于检测道路车辙深度,实现公路技术状况的科学评定。此类仪器于90年代末引入中国,并得到广泛应用,于2007年被正式写入交通运输部行业标准[2]。线激光路面车辙仪由线结构激光光源、数字图像采集装置、纵向测距传感器和计算机数字图像处理系统等部分组成。因车辙输出结果需经过仪器的多重处理和转换,量值影响因素复杂,故测量不确定度的分析与评定成为评价仪器计量性能和实施技术改进的关键。
1 测量原理
线激光路面车辙仪以道路横断面测点的高程测量为基础,通过规定的计算模型获得车辙深度值。测点高程基于三角测量原理实现,如图1所示。

图1 高程测量原理
图中Las为线结构激光器安装位置;Cam为相机安装位置;Pave为被测路面;a 为激光入射方向与相机光轴的夹角(观察角);β为激光入射方向与受光面法线的夹角(入射角);h为被测位置相对于基准路面的高程;d为激光线变形的有效成像长度;i为成像中对应测点位置的激光线变形量;L为相机镜头光心距成像物体的距离(物距);f为镜头焦距(像距);H为相机镜头光心距路面的垂直距离。
对于道路横断面上的每一个测点,仪器均能得到一个唯一的相对高程值h,由所有测点共同重建出车辙模型[3]。图2即为文献[3]中所提到的一种典型的车辙模型。

图2 典型车辙模型
由线激光车辙仪测量得到的各点高程值通过车辙计算软件[4]分析,可得到不同模型时的车辙深度值。
2 车辙计算模型
线激光车辙仪是实现路面横断面连续测量的仪器,对于典型车辙断面,常采用对车辙量值影响较大的5个关键点的相对高程进行车辙计算。其计算模型如下:
Drut=F(h)=A1h1+A2h2+A3h3+A5h5+A5h5+δ
(1)
式中:Drut为车辙深度;hi,i=1,2,…,5为5个关键测点的相对高程值;Ai,i=1,2,…,5为5个关键点的加权系数;δ为因关键点选取不准确造成的车辙深度计算误差。
3 高程测量的数学模型
线激光车辙仪利用CCD成像及模式识别技术,将路面车辙测量转化为基于高分辨率图像的测量,是数字摄影测量学的具体应用[5],其理论基础是光的直线传播特性。因此,可通过几何光学理论进行高程测量数学模型的推导。
3.1 理论计算模型
在图1中,存在以下几何关系:
(2)
式中:

代入式(2)得高程计算公式为:
(3)
物距L可进一步转换为镜头安装高度H的函数,如下式:
(4)
3.2 工程应用模型
由高程的理论计算模型知,从图像中测量值i计算得到路面测点的相对高程h,需经过复杂的非线性运算。工程中为应用方便,一般通过合理假设,建立线性模型加以描述。
对于特定的线激光车辙仪,集成安装后的L,β,f,a 均为常数,i通常为微米量级,镜头焦距为厘米量级,数量级相差较大。因此,式(3)中,icosa 项对于模型的影响较小,i与h接近线性关系。
简化模型可表示为:

(5)

4 不确定度评定
4.1 高程测量的不确定度
车辙横断面上测点高程的测量函数如式(3),高程测量的不确定度由各分量的不确定度合成[6],公式如下:

因为高程测量函数的复杂性和非线性,致使合成标准不确定度的计算非常复杂。可以用实验方法确定灵敏系数,即采用变化一个量,计量由此引起的高程的变化量来得到灵敏系数[7]。
对于绝大多数仪器,测点高程均采用式(5)的线性模型,高程测量的不确定度主要来源于线性估计过程。可通过以下方法评定其不确定度:
1)确定仪器参数a ,β,f,H,求测点高程的理论值;
2)求线性回归模型参数;
例如,给定的线激光车辙仪的仪器参数为:a=22°,β=80°,f=0.01m,H=1.5m,成像系统某型号相机的像元尺寸为6.7μm,车辙横断面高程的设计量程为75mm。
对式(5)的线性模型系数进行求解,得测点高程线性计算公式为:

(6)
相关系数:r=0.9985。
理论值及线性估计值的分布曲线如图3所示。

图3 理论值与线性估计值的分布
测点高程线性估计值及残差计算如表1所示。

表1 测点高程线性估计计算表
线性拟合的残差随着高程的增加呈规律性变化,残差绝对值的最大值为1.9120,出现在相对高程较小处。线性拟合结果及残差分布见图4。
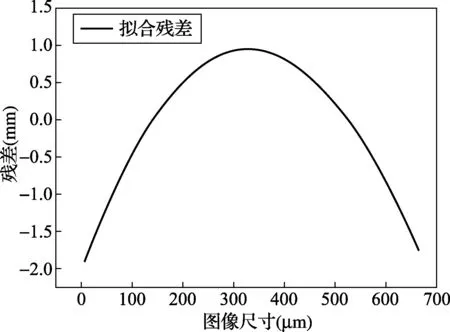
图4 线性拟合残差分布
上例中,采用式(6)的线性模型进行高程计算的标准不确定度为[8]:uh=0.8432。
4.2 车辙测量的不确定度
车辙深度计算模型如式(1),其中关键点为车辙断面的局部极值点,关键点决定了车辙断面的基本形态,对车辙的计算至关重要。对于线激光车辙仪,沿道路横断面高程测量是连续的,正常测量过程总能得到关键点,因此,可认为式中δ为零。即:
Drut=F(h)=A1h1+A2h2+A3h3+A5h5+A5h5
(7)
因为式(6)中各点高程测量原理及算法相同,各点高程测量强相关,Drut的测量不确定度可采用下式合成:
5 结束语
文中从线激光路面车辙仪的测量原理入手,对比分析了车辙理论计算模型及工程应用模型的异同,并采用实例阐述了测量不确定的评定方法。线激光路面车辙仪的测量原理决定了高程测量具有很好的连续性,由车辙断面关键点定位不准所引入的不确定度可忽略不计。因此,其测量不确定度主要来源于模型建立时的线性拟合过程。文中对线性模型的推导主要基于理论公式的模拟数据,实际应用过程中也可对大量的实验数据进行线性拟合来得到线性模型。通过不确定度分析,可以更深入的理解影响线激光车辙仪测值准确性的关键因素,进而在仪器设备的改进过程中加以应用。
[1] J.Laurent, M.Talbot, M.Doucet, “Road Surface Inspection using Laser Scanners Adapted for the High Precision Measurements of Large Flat Surfaces,”3dim, pp.303, First International Conference on Recent Advances in 3-D Digital Imaging and Modeling (3DIM ′97), 1997
[2] JT/T 677—2009车载式路面激光车辙仪[S].北京:人民交通出版社,2009
[3] JTG E60—2008公路路基路面现场测试规程[S].北京:人民交通出版社,2008
[4] 交通运输部公路科学研究所.路面车辙模型分析软件[P].中国:软著登字第0524950号,2013
[5] 张祖勋,张剑清.数字摄影测量学[M].武汉:武汉大学出版社,2012
[6] 倪育才.实用测量不确定度评定(第3版)[M].北京:中国计量出版社,2009
[7] 耿维明.测量误差与不确定度评定[M].北京:中国质检出版社,2011
[8] 刘庆,邵志新.回归分析的直线拟合不确定度探讨[J].中国测试,2009,35(3):41-44
[9] 陈果,周伽.小样本数据的支持向量机回归模型参数及预测区间研究[J].计量学报,2008,29(1):92-96
[10] 吴德会.基于最小二乘支持向量机的传感器非线性动态系统辨识[J].计量学报,2008,29(3):226-230
[11] 李庆忠,李春燕.合成不确定度的两种评估方法 [J].计量技术,2007(6):57-59
交通运输部计量质量研究项目:2012-318-223-250
10.3969/j.issn.1000-0771.2015.07.23
