圆面积公式推导难点及其解决之道的启示

俞正强

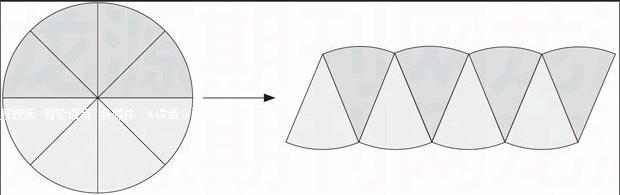
圆面积公式的推导不同于其他图形面积公示的推导，关键之处在于把一个圆形变成了长方形，这种变是学生很难接受的。

教师通常会通过上图的比较告诉学生：分得更多就会更像长方形，这就是无限接近的意思。但对学生而言，分得再细也还是曲线，只是由更短的曲线接起来而已。

数学专家会说，因为线是由点组成的，当分成点时，曲线就会变成直线。但问题是：由圆分割而成的始终是如下的形状。

当变成点，这个形状还有吗？长方形还在吗？

当然，对于这些想法，学生是不会讲出来的。因为他们已经习惯了听教师所说的。教师说变成长方形，就是长方形吧，何苦自寻烦恼！而这种想法正是教学的可怕之处。我们在教给学生知识的同时断了他们思想的冲动。因此，数学教师应该想办法纾解圆方（曲直）之间的纠结关系。

圆形变成长方形的困难究其根源是线的曲直问题。因此，在小学，有两节课可以为这个问题的纾解做比较好的铺垫。

铺垫一：线无曲直

小学四年级有一节课是“线的认识”。在这一节课中，很重要的一个内容是认识“线的基本属性为长短”。但在生活中，线除了有长短外，还有曲直、粗细之分。因此，要在这一课中让学生体会线无曲直、无粗细，明确曲直、粗细并非线的基本属性。

……

师：同学们，大家都说线分曲线和直线。

生：是的。

师：请大家说说你是怎样来区分曲线和直线的？

生：只要不直的就是曲线。

师：（两只手拿起一条线且拉直）同学们，这条线是什么线？

生：直线。

师：（两只手往中间靠拢）同学们，这条线是什么线？

生：曲线。

师：这条线一会儿是曲线，一会儿是直线，那这条线到底是什么线？

生：……（发呆了）

师：这条线变直、变曲的原因是什么？

生：是老师在拉，是老师的原因。

师：很好，那线自己是曲的，还是直的呢？

生：不知道，它自己只是线而已。

师：线自己有曲直吗？

生：没有。

整个过程颠覆了学生确定线有曲直的生活经验。因为在这一过程中，教师把生活中的线通过一个活动把它分为现象与本质。从现象上看，是有曲直的;从本质上看，却是无曲直的。这种关于现象与本质的讨论，是无法用语言给学生讲明白的。只有在活动中有所感悟，有所体会，有所惊诧，有所疑惑，恰是在惊诧和疑惑中，才会更好地体会关于线的现象与

本质。

原来的关于线有曲直的根深蒂固的观念被动摇，继而慢慢地树立起关于线无曲直的认识。线的曲直由“二”的状态变成“一”的状态。

铺垫二：圆是几边形

在小学五年级“圆的认识”这一课中，圆的特征是曲线。这是与之前学过的图形在外观上的最大不同。因此，对圆的认识，有必要在直线与曲线上再一次联结，使四年级“线的认识”一课中埋下的“线无曲直”的种子得到伸展。

材料：将正三边形每边的中间折断，会得到六边形，然后将每边的中间折断，得到十二边形，依次不断进行，得到下图。

问题讨论

问题1：以此不断，一直到最后，最后会是个什么图形？

结论：最后是一个圆。

问题2：圆是几边形？

观点1：圆是无数边形。

观点2：圆是一边形。

讨论1：为什么会认为圆是无数边形？

正三边形  正六边形  正十二边形  正二十四边形，

不断分边，越多越圆，因此，圆是无数边形。

讨论2：那圆是一边形的理由呢？

没有理由，一看就是一边。

讨论3：无数边是由观察推想出来的，是无数条直边。

一边形是观察来的，是一条曲边。那谁对呢？

结论：都对，无数条直边组成一条曲边。

这个结论非常重要，从小学四年级对曲直边线的模糊，到五年级的曲直融合，对线的认识有了渐趋完整的认识。

如前所述，公式推导的难点在于线的化曲为直，因为已经有了两个铺垫，即线无曲直，曲由直来，再来理解化曲为直，是十分自然而然的。

这个例子可以说明：

（1）圆形转化成长方形，从表象上来看，是形的问题，实质上是线的问题。线化曲为直的可理解决定形化圆为方的可理解。

（2）一节课的难点，如果之前不铺垫或在这几个点上略过，本质上说这节课的难点就会失去突破的机会。所谓的“突破”也只是学生无奈的记忆而已。

因此，数学课真的不是那么好上的。学生觉得数学难，可能真正难的是教师不知道今天的困难是由昨天的无知造成的。

（责任编辑：孙建辉）