盲信号分离技术及算法研究

王 钢，孙 斌

（哈尔滨工业大学通信技术研究所，黑龙江哈尔滨150001）

盲信号分离技术及算法研究

王 钢，孙 斌

（哈尔滨工业大学通信技术研究所，黑龙江哈尔滨150001）

盲信号分离是只依靠传感器观测到的混合信号来估计源信号的一门技术。介绍了盲信号分离的三种基本混合模型，重点阐述了正定线性瞬时盲分离的成熟算法，简单总结了目前针对欠定、单通道混合信号的常用盲分离方法，最后展望了盲信号分离技术发展的难点、趋势和应用。

盲信号分离（BSS）；混合模型；盲分离算法；单通道盲分离

0 引言

盲信号分离（BSS）亦称独立分量分析（ICA），是在对源信息和传输通道完全未知的条件下，仅根据观测的混合信号矢量来提取源信号各分量的一种信号处理方法。1986年，法国著名学者Herault和Jutten完成盲信号分离的先驱性工作［1］，并于1991年在Signal Process上发表了著名的H-J盲分离算法［2-4］。之后Tong［5］初步探讨了多阶累积量分离算法，Comon［6］提出了独立分量分析，Bell和Sejnowski提出信息最大化算法（Informax）［7］，Lee提出扩展信息最大化算法（Ex Informax）［8］，Amari提出梯度互信息最小化法［9］，Hyvarinen等提出固定点算法FastICA［10］。1996年清华大学出版了张贤达的《时间序列分析——高阶统计量方法》。焦卫东等将盲分离技术应于信息安全领域，李加文等提出在频域瞬时盲分离/主成分分析/瞬时混合盲分离结构，黄青华提出基于贝叶斯估计的状态空间分离模型求解盲分离［11］。

进入21世纪以来，盲信号分离从正定混合到欠定混合甚至到更加复杂的单通道混合的研究。混合模型也从线性瞬时混合方式扩展到线性卷积混合方式再到非线性混合方式。而线性瞬时混合是其他混合方式的基础，因此本文予以重点介绍。

1 盲信号分离的混合模型

根据源信号与传输信道混合方式的不同，盲信号分离的混合模型主要分线性与非线性两类。其中线性混合模型可以细分为线性瞬时混合模型和线性卷积混合模型。

1.1 线性瞬时混合模型

线性瞬时混合指观测信号仅仅是源信号的简单线性组合，不考虑源信号的时延特性，是最简单的一种混合方式，其表达式为：

式中，X=（x1，x2，…，xm）T指各传感器观测到的源信号的不同混合信号矢量，S=（s1，s2，…，sn）T是源信号矢量，H=（hi，j）为M×N维混合矩阵，hi，j为常数。N=（n1，n2，…，nm）为加性噪声，可忽略不计。

线性混合模型的分解过程表达式为：

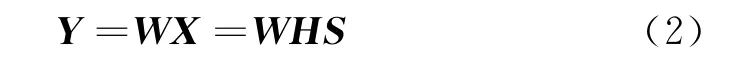
式中，W=（wi，j）为N×M维分离矩阵，理想情况下W=H-1，这时Y=S。一般情况下，分离后的Y=DPX，D为对角矩阵，P为交换矩阵。式（2）说明盲信号分离本质上存在不确定性，主要表现在输出信号幅度和顺序的不确定性，但不会影响盲信号分离技术的应用，因为信号携带的信息是包含在源信号的波形特征中。盲信号分离系统示意图如图1所示。

图1 盲信号分离原理框图

1.2 线性卷积混合模型

与线性瞬时混合方式相比，线性卷积混合方式更接近实际信号传输的多径效应，考虑了源信号的不同传输时延特性，观察结果为源信号与传输信道的卷积，其数学表达式为：

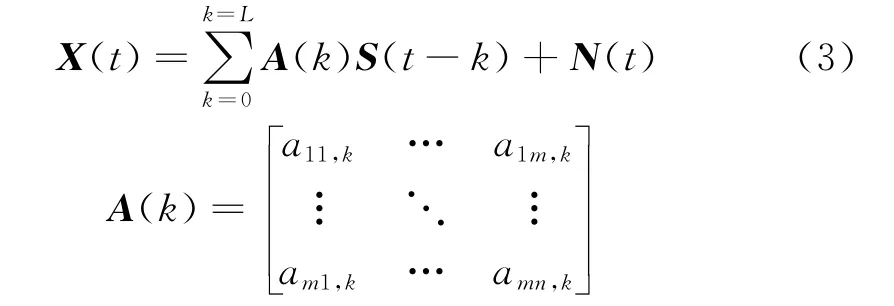
式中，k∈［0，L］，A（k）表示延时为k的混合信道矩阵，当L=0时，线性卷积混合方式就变为线性瞬时混合方式。

1.3 非线性混合模型

在实际场景中，信号的线性混合方式几乎不存在，一般为准线性混合或者为非线性混合方式。非线性混合方式主要分为两类，对应的模型有一般非线性混合模型和后非线性混合模型（PNL）。一般非线性混合模型的数学表达式为：

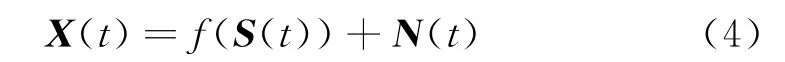
式中，f为一个Rn到Rm的非线性映射。

后非线性混合模型是线型混合模型与非线性混合模型的一种组合推广，即源信号先经线性混合后再经非线性混合。其数学表达式为：

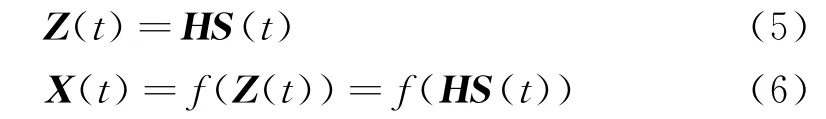
后非线性的混合方式的分离过程为混合过程的逆过程，即对观测到的信号先进行非线性分离，后进行线性分离。表达式为：

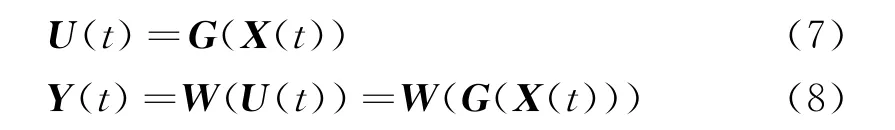
2 正定盲信号分离常用算法

正定盲信号分离算法中，观测信号的维数M与源信号的维数相等，即：M=N。欠定盲信号分离算法中，M＜N。如果M=1，则称为单通道混合盲分离。

2.1 线性瞬时盲信号分离算法

2.1.1 联合对角化算法（JADE）

联合对角化（JADE）算法是批处理算法的典型代表，是四阶盲辨识（FOBI）算法的改进。该算法通过对信号的四阶累积量的特征分解和联合对角化得到分离矩阵和分离信号（源信号的估计）。但算法需要的计算存贮空间较大，不适于高维盲分离。

正交联合对角化盲分离的基本思想是利用观测信号的统计特性构造具有可联合对角化结构的目标矩阵组，建立起混合矩阵、白化矩阵、分离矩阵之间的关系，再通过联合对角化方法估计混合矩阵。非正交盲分离则直接根据观测信号构造目标矩阵、直接进行非正交联合对角化估计，而不做白化处理。JADE盲分离算法的一般实现步骤如下：

1）求观测信号矢量协方差Rx，计算一个白化矩阵w；

2）求解观测信号矢量的白化过程z（t）=wx（t）的四阶累积量，再计算最大不超过n的两个特征值：Ne=（λr，mr|1≤r≤n）；

3）用一个正交（酉）矩阵把集合Ne联合对角化；

4）混合矩阵A的估计为：A=wU。

联合对角化盲分离的原理如图2所示。

图2 JADE盲分离算法的原理框图

2.1.2 信息最大化算法（Informax）

信息最大化算法是自适应算法的典型代表。Informax是基于信息论的一种算法，该算法核心思想是通过非线性函数使分离信号的嫡最大化，即分离信号之间尽可能地相互独立。其原理如图3所示。

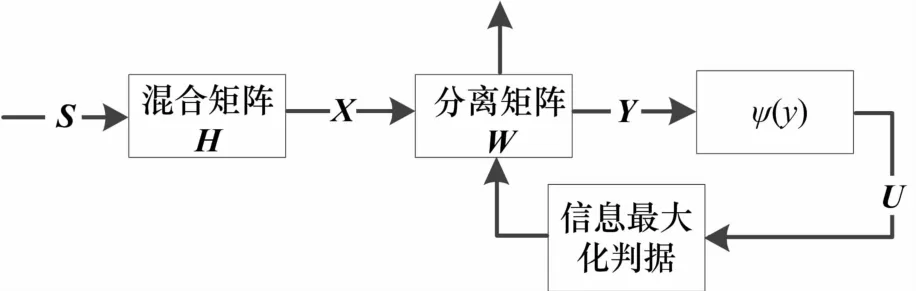
图3 Informax盲分离算法的原理框图

图3 中，ψ（y）是单调可逆的非线性转换函数，U=（u1，u2，…，un）为非线性输出。Informax算法的独立性判据就是信息传输的最大原则，更新分离矩阵H改变分离信号Y，使输出U中各分量的总嫡达到极大值，这时分离信号Y各分量之间互信号最小，也即各分量之间独立性最大，分离信号更接近源信号S。分离矩阵的自适应公式为：

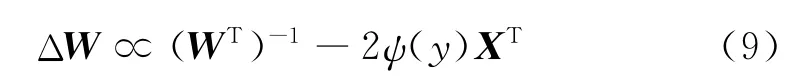
式（9）中的迭代公式是基于随机梯度得到的，需要矩阵求逆，计算效率低，后由Cardoso和Cichocki等改进为：

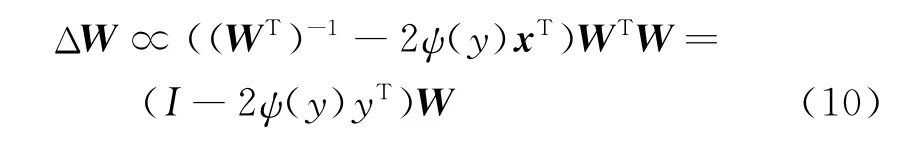
式中，ψ（y）=tanh（y）。

经典的自适应算法有扩展的信息最大化算法（ExInformax）、非线性主量分析（NLPCA）、互信息最小化算法（MMI）等，它们都具有统一的自适应算法更新公式ΔW∝（I-2ψ（y）yT）W，只是非线性函数ψ（y）的选择不同，这里不再赘述。

2.1.3 快速算法（FastICA）

尽管自适应算法能适应环境的变化，但收敛速度较慢，其收敛速率主要取决于学习速率，且学习速率选择不当时可能引起算法不收敛。

芬兰学者Hyvarinen于1997年提出基于峭度的FastICA算法，1999年提出基于负嫡的改进FastICA算法。基于负嫡的FastICA算法是一个曰棒的度量，能较好地克服因某个不准确的值可能引起峭度发生巨大变化的缺点。

FastICA算法是基于非高斯性最大化原则得到的一种批处理算法，它的收敛速率快且易于实现。下面举例以四阶累积量作为输出信号相互独立的判据来说明FastICA算法流程：第一，对观测信号x（t）去均值预处理后进行白化处理。第二，采用FastICA算法分离出源信号各分量，具体步骤如下：

1）任取初始向量ui（0），且满足‖ui（0）‖22= 1（k=0）；

2）求ui（k+1）=E（z（ui（k）Tz）3），其中，E（·）用对z（t）的采样点求均值代替；

3）归一化ui（k+1）/（‖ui（k+1）‖2）→ui（k+1）；

4）若|ui（k+1）ui（k）T|≠1（或者不接近1），返回步骤2）继续迭代，否则迭代结束，令ui=ui（k+1）；

5）提取yi（k）=uTiz（k）作为si的估计。

FastICA的基本原理如图4所示。

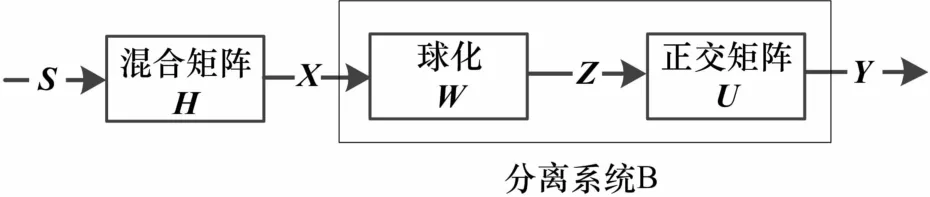
图4 FastICA盲分离原理框图

球化过程可以使z（t）各分量之间不相关，且方差为1。正交变换过程使分离信号之间尽可能相互独立。

2.2 线性卷积盲信号分离算法线性卷积混合模型可以更好地刻划信号在真实环境中的传播特性，其盲分离算法可以分为两类：时域盲分离算法和频域盲分离算法。

2.2.1 时域盲分离算法

1）转化为线性瞬时盲分离

重新定义源信号为：

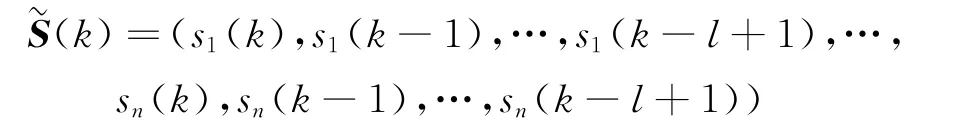
重新定义观测信号为：

2）Bussgang算法

Bussgang算法的核心思想是使分离后的信号经过一个非线性函数后用其输出与输入信号做差，用该差值调整分离矩阵。该算法的优点是简单易实现，缺点是存在局部极小点，收敛解可能有误。根据非线性函数的不同，Bussgang有不同类型，如Godard算法，B2G算法等。

3）高阶统计量方法

高阶统计量方法具体可分为显累计量法和隐累计量法。前者利用高阶累计量作对比函数，使用随机梯度法求解分离矩阵。后者利用神经网络和非线性函数来近似反映高阶统计量，逐步更新分离矩阵。

2.2.2 频域盲分离算法

根据时域卷积对应频域乘积的理论基础，将时域卷积转换到频域乘积而不改变混合矩阵。实际应用中一般采用短时傅里叶变换将信号变换到若干个频点上，解混后再变换回时域，从而实现卷积盲信号分离。该算法优点是计算量小，缺点是分离信号存在顺序上的不确定性，在时域中可能不能正确拼接。

2.3 非线性盲信号分离算法

非线性盲分离要比线性盲分离更加复杂。常用的非线性分离算法有自组织映射（SOM）算法、Bayesian集合学习算法和遗传算法。

1）自组织映射算法：算法的核心思想是抽取观测信号的非线性特征，确定可能的非线性函数从而达到分离信号的目的。优点是灵活性高，缺点是当信源增加时，计算复杂度呈指数增加。

2）Bayesian集合学习算法：亦称为多变量贝叶斯学习法，是利用一个适于估计后验分布参数的极限分布来实现盲分离。

3）遗传算法（GA）：为更好地估计非线性函数参数，避免局部极小值问题，Rojas等人引入了遗传算法，从全局出发逼近全局最优解，该算法比传统的梯度法收敛速度更快，稳定性更好。

3 欠定盲信号分离算法

欠定盲分离是一个病态分离，混合矩阵的逆矩阵不存在，分离结果通常不唯一。目前欠定盲分离的常用算法有基于信号稀疏性的算法、Bayesian方法和二元掩蔽法。

1）基于信号稀疏性的算法：若源信号满足稀疏性，混合信号具有线性聚类特性，此时可以用聚类法估计混合矩阵以实现欠定盲分离。如果源信号在时域不满足稀疏性条件，可将信号通过某种变换使其在变换域中满足稀疏性，实现信号分离后再反变换回时域。目前最常用的变换主要有傅里叶变换、短时傅里叶变换、小波变换、离散余弦变换等。

2）Bayesian方法：Bayesian方法充分利用了源信号的概率分布，即使源信号非稀疏，从而实现盲分离。Bayesian方法一般适用于相互独立的实源信号的欠定盲分离。

3）二元掩蔽法：二元掩蔽法的主要思想是在变换域上使混合信号尽可能稀疏，再通过构造二元掩蔽函数将欠定问题转化为正定问题。二元掩蔽法计算简单分离效果较好，适于线性盲分离，该方法也是目前最常用的盲分离算法之一。

4 单通道混合盲信号分离算法

单通道盲分离（SCBSS）是在观测信号数目为1的条件下的欠定盲分离，是一个更加病态的盲分离问题。SCBSS必须已知源信号的某些先验信息才可进行分离。下面简单介绍几种目前研究较多的单通道混合盲信号分离算法。

1）变换域滤波法：将时域混叠，通过傅里叶变换、小波变换、循环谱等，在变换域中分离信号后再变换到时域，该方法的本质为变换域滤波。

2）基函数法：基函数单通道盲分离法分为两个阶段，训练阶段和分离阶段。训练阶段采用没有混合的源信号作为训练数据，用某种经典算法学习得到源信号的基函数作为先验信息。分离阶段基于上述基函数采用最大似然函数优化方法估计源信号。

3）基于粒子滤波的算法：粒子滤波的基本思想是利用离散样本点替代后验分布，将贝叶斯积分转换为求和，从而可实现未知变量的后验概率分布，不断利用输入的信号实现参数与符号的联合估计。粒子滤波在处理非线性、非高斯问题中优势明显。

除了上面介绍的几种方法外，还有一些其他方法，如因子分析、线性预测LP、恒模算法、PSP算法等。

5 结束语

在盲信号分离领域，线性盲分离理论的发展相对比较成熟，而非线性盲分离、欠定盲分离还有许多问题函待解决。此外，含噪盲分离（特别是低信噪比情况下）、复数情况下的盲分离、单通道盲分离均为研究的热点与难点。目前盲信号处理技术已在生物医学、雷达信号分选、电子侦查、图像处理等领域广泛应用。与实际应用的结合，会使盲信号分离技术获得更强大的生命力和更广阔的应用前景。■

［1］ Jutten C，Herault J.Space or time adaptive sign al processing by neural network models［C］∥Snowbird，Utah，USA：Intern.Conf.on Neural Network for Computing，1986：206-211.

［2］ Common P，Jutten C，Herault J.Blind separation of sources，part II：problems statement［J］.Signal Processing，1991，24（1）：11-20.

［3］ Jutten C，Herault J.Blind separation of sources，part I：an adaptive algorithm based on neuromimetic architecture［J］.Signal Processing，1991，24（1）：21-30.

［4］ Sorouchyari E.Blind separation of sources，part III：stability analysis［J］.Signal Processing，1991，24：21 -29.

［5］ Tong L，Liu R，Soon V.Indeterminacy and identifiability of blind identification［J］.IEEE Transactions on Circuits and Systems，1991，38（5）：499-509.

［6］ Comon P.Independent component analysis，a new concept［J］.Signal Processing，1994，36：287-314.

［7］ Bell AJ，Sejnowski TJ.An information maximization approach to blind separation and blind deconvolution［J］. Neural Computation，1995，7（6）：1004-1034.

［8］ Lee T，Girolami M，Sejnowski T.Independent component analysis using an extended information algorithm for mixed sub-gaussian and super-gaussian sources［J］. Neural Com Putation，1999，9（7）：1483-1492.

［9］ Amari S，Cichocki A.Adaptive blind signal processingneural network approaches［J］.Proceedings of IEEE，1998，86（10）：2026-2046.

［10］Hyvarinen A，Oja E.A fast fixed-point algorithm for independent component analysis［J］.Neural Computation，1997，9（7）：1483-1492.

［11］黄青华.基于源信号模型的盲分离技术研究及应用［D］.上海：上海交通大学，2007.

Research on blind signal separation technology and algorithm

Wang Gang，Sun Bin
（Harbin Institute of technology，Communication Research Center，Harbin 150001，Heilongjiang，China）

BSS is used to estimate and separate the source signals only from the observed signals by sensors.The BSS's three essential math models are presented.The mature algorithms of positive-definite BSS technology is mainly introduced.Some common algorithms of underdetermined signals and single-channel mixed signal are briefly summarized.Finally，BSS's challenges，trends and applications are forecasted.

blind signal separation；mixed model；BSS algorithm；single-channel BSS

TN971

A

2014-08-20；2015-03-18修回。

王钢（1962-），男，教授，主要研究方向为数据通信。