球铰接杆式支撑臂斜拉索组件的参数影响分析

黎彪 刘志全 程刚 丁锋

(中国空间技术研究院，北京 100094)

球铰接杆式支撑臂斜拉索组件的参数影响分析

黎彪 刘志全 程刚 丁锋

(中国空间技术研究院，北京 100094)

文章分析了斜拉索倾角对支撑臂剪切刚度和扭转刚度的影响，给出了一定横杆长度下斜拉索倾角的最佳取值范围。以支撑臂杆件不发生屈曲失效和支撑臂在最大负载下不发生坍塌为准则，给出了斜拉索预张力的上下限。基于Hertz接触理论，推导了斜拉索预张力与球铰副接触刚度的关系，将关系式引入支撑臂单元段的有限元模型中，进行了模态分析，给出了斜拉索预张力对单元段一阶弯曲频率的影响曲线。分析结果表明，单元段一阶频率先随着斜拉索预张力的增加而增加，但当预张力超过一定值后，预张力的增加反而会使一阶频率降低;得到了斜拉索预张力优选范围。推导了锁定装置解锁力与支撑臂收拢时所需外力矩的关系，利用ADAMS软件对展开/收拢过程的扭矩进行了仿真，对支撑臂单元段展开/收拢过程中所需力矩进行了试验测试，试验结果表明，力矩的理论计算及仿真与试验结果基本吻合，误差在3%以内，证明了理论计算与仿真的正确性。研究结果为球铰接杆式支撑臂中斜拉索组件设计提供了理论依据。

球铰接杆式支撑臂；斜拉索；预张力；锁定力；解锁力

1 引言

球铰接杆式支撑臂(下文简称“支撑臂”)在大型柔性太阳翼、太阳帆等领域具有广泛的应用前景。斜拉索组件是支撑臂的关键组成部分，为支撑臂提供扭转刚度和剪切刚度[1]。斜拉索组件的结构参数(斜拉索倾角)和力学参数(斜拉索预张力)对支撑臂刚度有较大影响，锁定装置的锁定力、解锁力决定着支撑臂的展开/收拢过程中所需外力矩。因此，对斜拉索组件结构和力学参数的影响分析将为支撑臂的设计和工程应用提供重要参考。

文献[2]根据工程经验给出了支撑臂剪切刚度、扭转刚度的经验公式，但公式中有关系数与支撑臂的构型和长度等因素相关，对不同的支撑臂均需要进行标定。文献[3]以支撑臂的一个侧面为研究对象，指出斜拉索预张力存在最优值使结构的频率最大，文献[4]分析了斜拉索预张力对支撑臂弯曲刚度的影响，但文献[3]、[4]均忽略了预张力对球铰副接触刚度的贡献。文献[5]设计了一种典型的斜拉索组件锁定装置，阐述了锁定装置的工作原理，但未给出锁定装置中锁定力、解锁力的设计依据。文献[6]推导了支撑臂展开过程中所需的外力矩，但未给出外力矩与锁定装置锁定力之间的关系。

针对上述问题，本文将基于等效连续体模型分析斜拉索倾角对支撑臂剪切刚度和扭转刚度的影响；基于Hertz接触理论和有限元分析获得斜拉索预张力对支撑臂一阶弯曲频率的影响关系；分析锁定装置锁定力与单元段展开时所需外力矩的关系，以期为球铰接杆式支撑臂中斜拉索组件的设计提供理论依据。

2 斜拉索组件的组成及工作原理

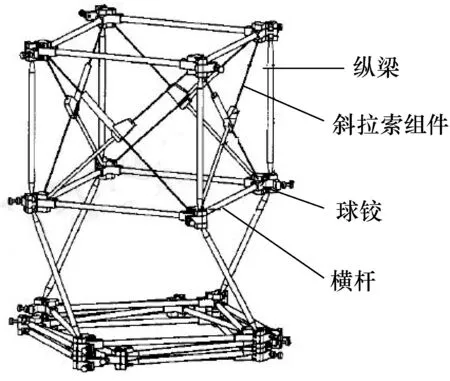
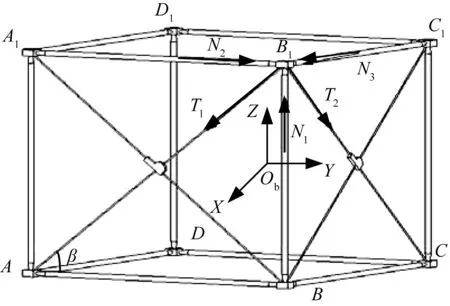
图1 球铰接杆式支撑臂的组成Fig.1 Configuration of ADAM-type mast

支撑臂组成如图1所示，其中单元段侧面斜拉索组件的组成如图2(a)所示。单元段中沿展开方向的杆件AA1、BB1等杆件为纵梁，垂直于展开方向的AB、BC等杆件为横杆，横杆与纵梁之间采用球铰副连接。单元段的每个侧面包含了1个锁定装置和4段拉索。以侧面ABB1A1为例，拉索1和拉索2为同一根连续的拉索，可绕锁定装置中的滑轮运动，拉索3两端分别固定在锁定装置和横向框架球铰处，拉索4采用与拉索3相同的连接方式。锁定装置的结构主要包括滑轮、锁定簧片、锁定球和壳体，如图2(b)所示。

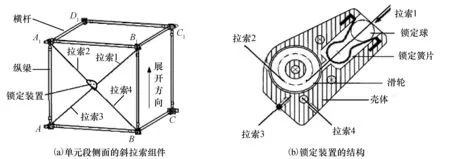
图2 斜拉索组件的组成Fig.2 Configuration of diagonal component

支撑臂展开到位的锁定是通过锁定装置实现的。假定下横向框架ABCD固定，外力矩驱动上横向框架A1B1C1D1旋转升高，实现单元段的展开。在展开过程中拉索2逐渐变长，拉索1逐渐变短，拉索1和拉索2的拉力始终相等。随后，当固联在拉索1上的锁定球接触到锁定簧片时，拉索2的拉力必须大于锁定簧片的阻力与拉索1拉力之和，从而使锁定球进入锁定簧片组成的凹槽中，实现了单元段的锁定。在整个展开过程中，拉索3和拉索4始终处于随动状态。反之，在收拢过程中，拉索1的拉力需大于锁定簧片的阻力和拉索2的拉力之和，将锁定球从凹槽中释放，实现单元段的解锁。

3 斜拉索倾角对支撑臂扭转刚度和剪切刚度的影响

文献[7]基于等效连续体模型，推导了支撑臂的剪切刚度GA和扭转刚度GJ分别为

(1)

式中Ec为斜拉索的弹性模量；Ac为斜拉索横截面的面积；斜拉索倾角β定义为图2(a)中拉索3与横杆AB的夹角；s为横杆长度。由式(1)可知，GA与Ec和Ac成正比；GJ与GA成正比，其比例系数为s2。

当斜拉索的材料与形状一定时，EcAc为一定值(试验件的EcAc=105N)，可获得β对GA和GJ的影响曲线，如图3所示。

图3 斜拉索倾角β对剪切刚度GA和扭转刚度GJ的影响Fig.3 Influence of diagonal obliquity on shear stiffness and torsion stiffness

从图3(a)可知，GA随β增加先增加后减小。tanβ在0.57～0.9时(对应的β为29.7°～42.0°)，GA为最大值的90%～100%。从图3(b)可知，GJ随着β增加先增加后减小，另外，随着s的增加，GJ峰值对应的β也增加。以文献[8]中s=0.8m的试验件为例，GJ为最大值的95%～100%时，对应tanβ在0.5～0.85之间(β为26.6°～40.4°)。

综合β对GA和GJ的影响，可得在s=0.8 m情况下，β的最佳取值范围为29.7°～40.4°。

4 斜拉索预张力上下限的确定

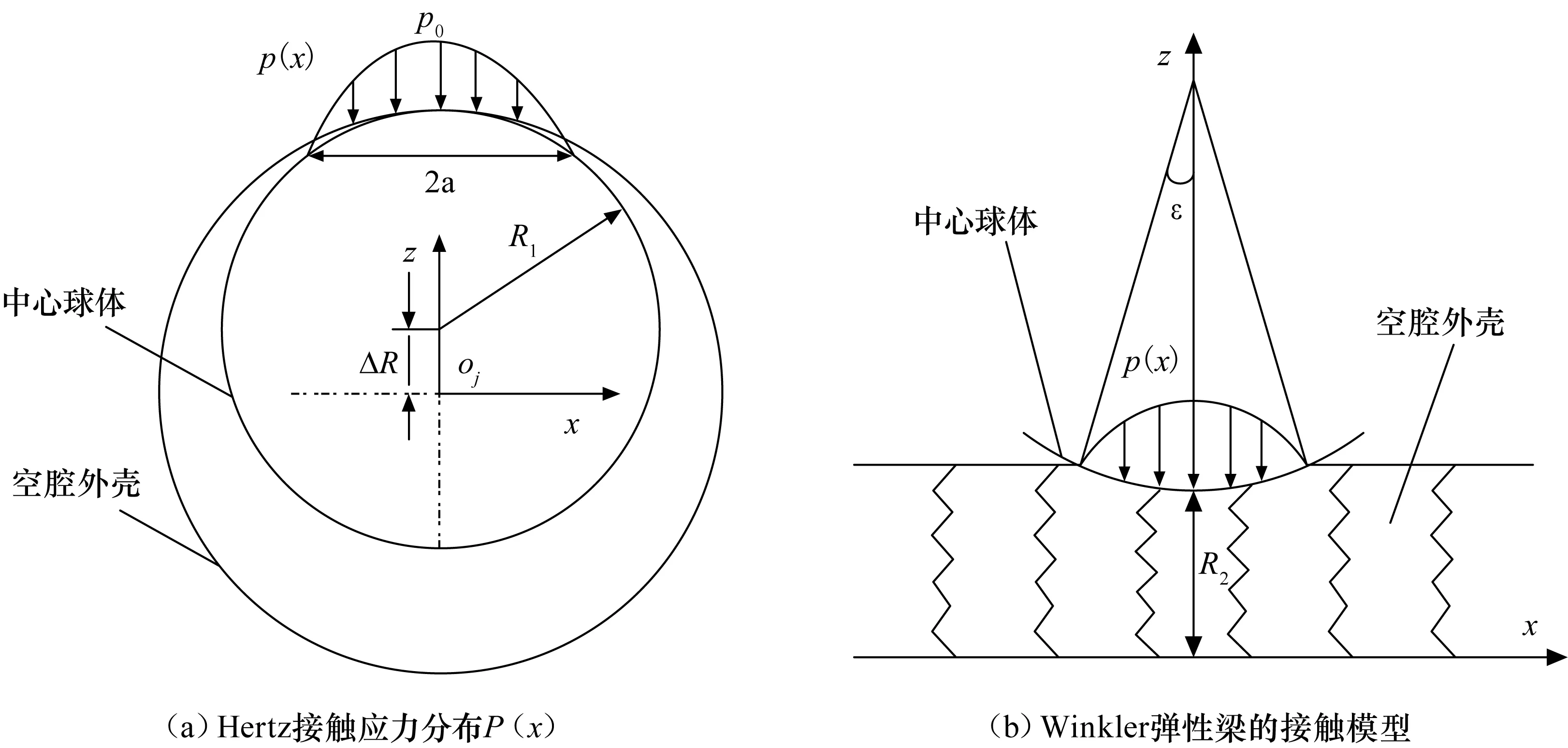
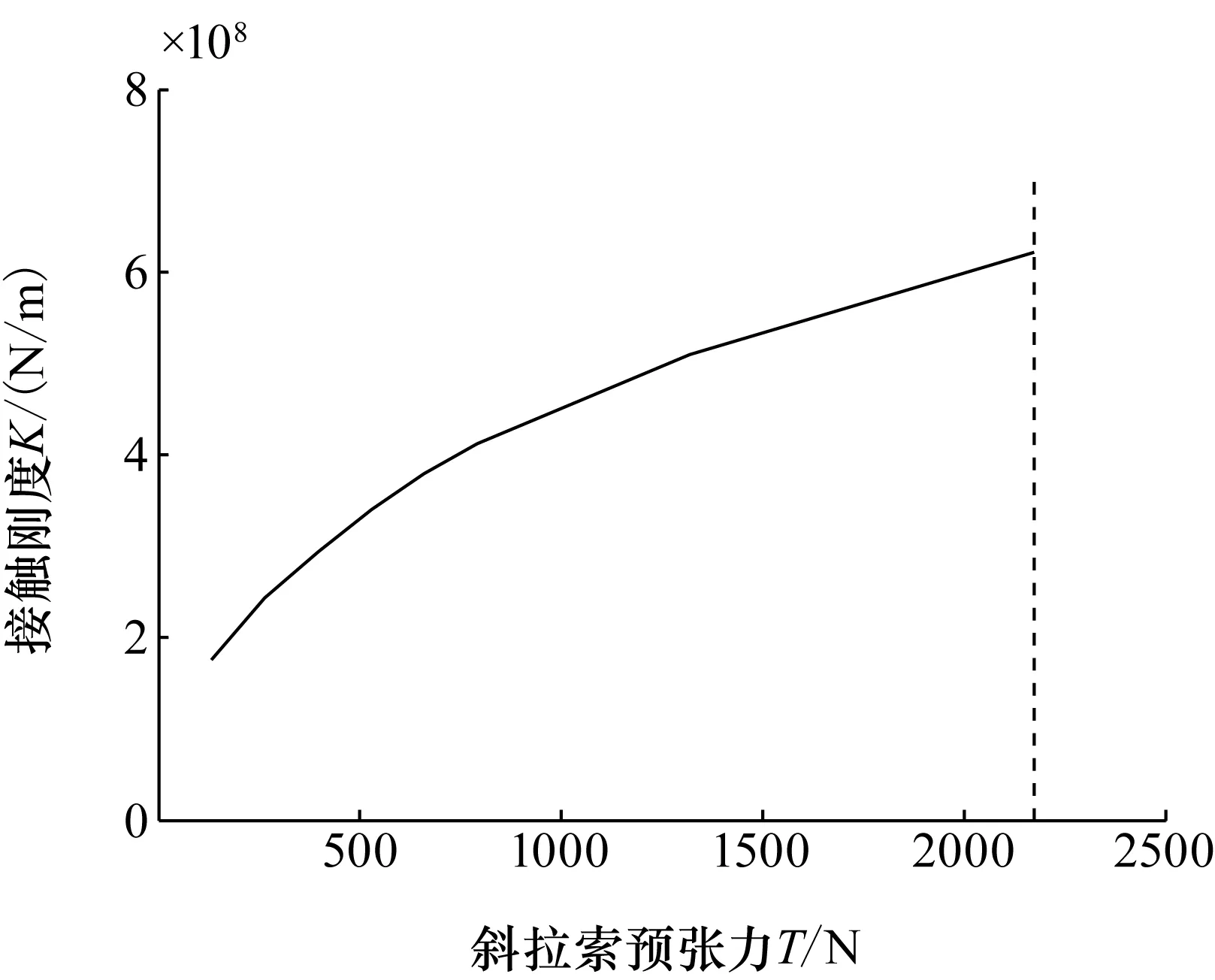
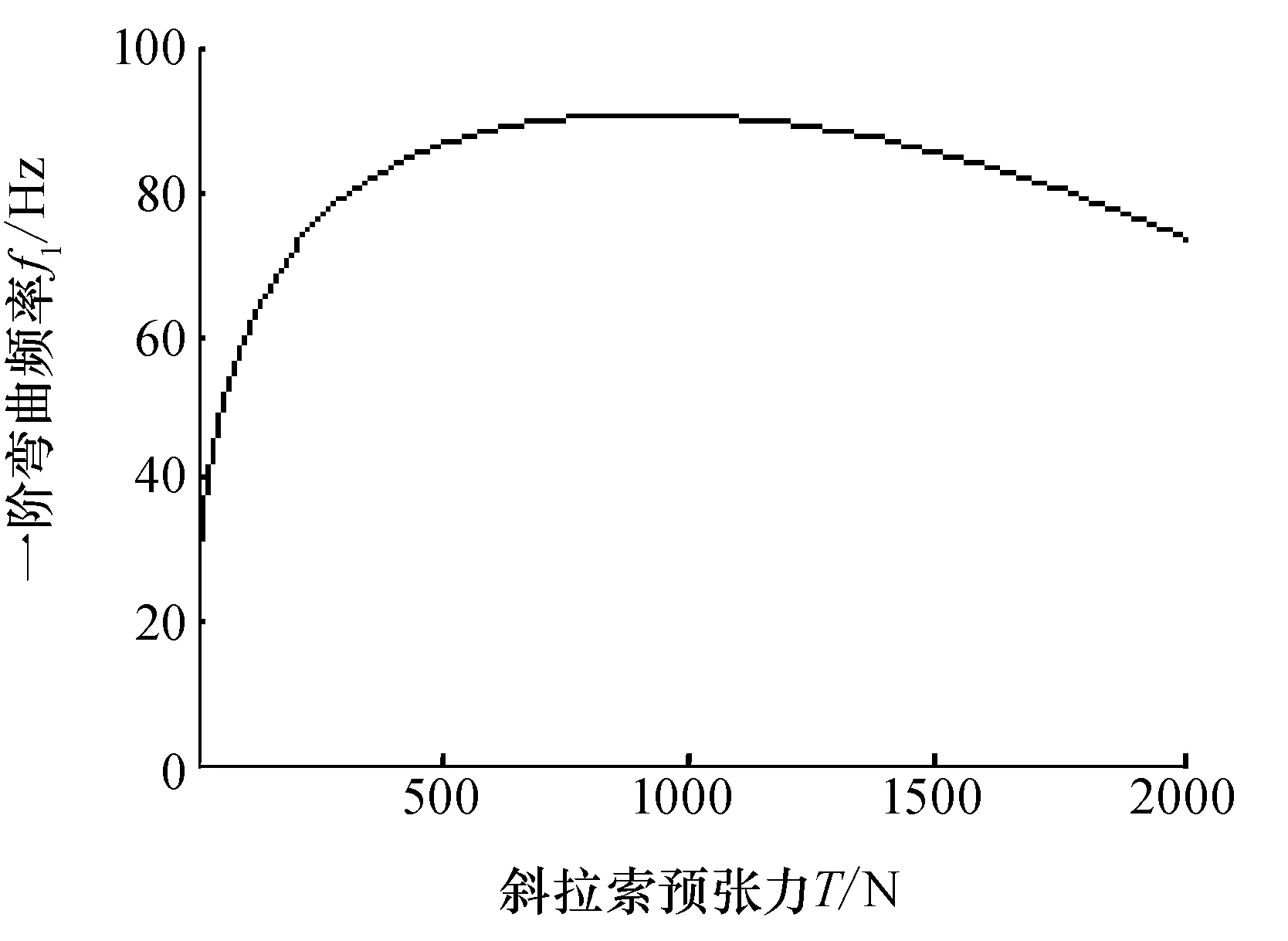
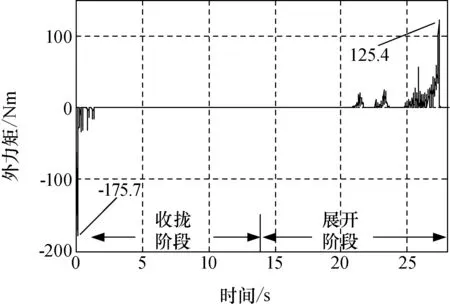
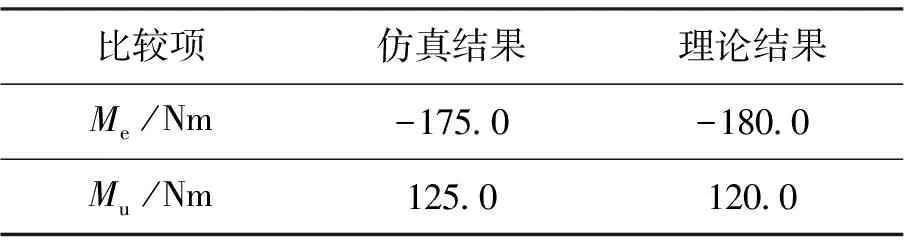
为防止支撑臂发生杆件屈曲失效，防止支撑臂在最大负载条件下因斜拉索松弛而导致支撑臂结构的坍塌，必须控制斜拉索预张力T的取值范围Tmin

(2)

式中Je为支撑臂的等效转动惯量；mt为末端负载质量；L为支撑臂的总长度；ξ为在轨运行中支撑臂最大角加速度；l为纵梁的长度。

对于两端为铰支的纵梁，发生屈曲的临界压力Pcr为

(3)

式中El为纵梁的弹性模量；Il为纵梁的截面惯性矩。Tmax与Pcr的关系为[8]

(4)

由式(3)和(4)可得Tmax为

(5)

5 斜拉索预张力对支撑臂弯曲刚度的影响分析

5.1 T对球铰副接触刚度K的影响

本文在文献[9]的基础上分析T对球铰副接触刚度K的影响。假设球铰副的中心球体压力分布

服从Hertz接触理论，而球铰副中空腔外壳简化成厚度为R2的Winkler弹性梁。以球铰副的中心球体为研究对象，其与空腔外壳的接触应力分布如图4(a)所示，接触应力p(x)为

(6)

式中p0为接触中心点的接触应力；x为接触面上任一点到接触中心的距离；a为Hertz接触区的半宽度。

图4 球铰副接触应力Fig.4 Contact stress for spherical joint

以球铰副的空腔外壳为研究对象，其受力情况如图4(b)所示，其中ε为接触半角，而Hertz接触理论中存在以下假设

(7)

式中 ΔR为空腔外壳和中心球体的间隙，如图4(a)所示；δ为接触时最大压缩量。

由于球铰副中空腔外壳和中心球体半径相差很小，则由图4(b)可以得到a和ε的关系为

(8)

球铰副的总接触力P为

(9)

根据Winkler弹性梁假设，任意点的接触应力为

(10)

式中E为Winkler弹性梁的弹性模量；u为该点沿z方向的弹性位移。

由对称性可知，中心点处基础梁的法向位移u0=δ/2，则可得p0和δ的关系为

(11)

应用式(6)～(11)，可得到基于Winkler弹性梁模型的球铰副总接触力P为

(12)

若球铰副中空腔外壳和中心球体之间施加有外部载荷F0，P将抵消外部载荷，此时球铰副的接触刚度K为

(13)

图5 球铰副接触刚度拟合曲线Fig.5 Contact stiffness of spherical joint

根据式(4)、(12)、(13)，可得到T对K的影响曲线。以文献[8]中试验件作为研究对象(试验件状态为横杆长度s=0.8 m，锁定装置的锁定力Fd=100 N，解锁力Fu=150 N。下文提及的试验件状态均与此一致)，支撑臂中球铰副参数为R1=6 mm，ΔR=0.05 mm。

由式(5)可知T需满足T<2 182 N(由于在轨时支撑臂的最大角加速度未知，本文没有计算斜拉索预张力的下限值)。按式(12)和式(13)可得T对K的影响曲线如图5所示。

从图5可知，在斜拉索预张力T的上限控制范围内，接触刚度K随T的增加而增加。

5.2 考虑球铰副接触刚度情况下T对支撑臂弯曲刚度的影响分析

图6 预张力对一阶弯曲频率的影响Fig.6 Effect of preload on bend stiffness for a bay

支撑臂是由相同的单元段叠加而成。T对单元段刚度的影响趋势与对支撑臂整体的影响趋势相同。因此，本文仅分析T对典型单元段的弯曲刚度影响，而弯曲刚度用一阶弯曲频率f1进行表征。仍以前文提及的试验件为研究对象，利用ANSYS软件对单元段进行有限元建模，将公式(13)引入模型中，随后进行模态分析，利用MATLAB与ANSYS联合仿真，获得T对f1的影响曲线如图6所示。

由图6可知，f1先随着预张力T的增加而增加，当T超过700 N后，T继续增加反而会使f1降低。其原因是当T>700 N后，预张力对支撑臂杆件的刚度削弱效果起主导作用。另外，从图6可得到试验件的T的优选值为500～700 N。

6 锁定装置力学参数与支撑臂展开/收拢时所需外力矩的关系

6.1 理论计算

图7 单元段展开过程的受力分析Fig.7 Static analysis of lock for a bay

假定下横向框架ABCD固定，上横向框架A1B1C1D1在驱动力矩Me驱动下展开到位实现锁定。在临近锁定时，上下横向框架的相对转角非常小，可认为AA1杆仍垂直于横向框架的平面。考虑到对称性，仅分析球铰B1的受力情况，如图7所示。

作用在球铰B1上的力有拉索拉力T1和T2，纵梁BB1的压力N1，杆B1A1的压力N2，杆C1B1的压力N3，若以球铰及上横向框架组成的整体为研究对象，则有

(14)

式中MT1和MT2分别为T1和T2绕Z轴的力矩；Me为锁定时所需的外力矩。由式(14)可得

(15)

式中Fd定义为锁定装置的锁定力，Fd=T1-T2。

同理，可以得到收拢瞬间外力矩Mu与解锁力Fu的关系为

(16)

式中 锁定装置的解锁力Fu=T2-T1。

式(15)和(16)分别为支撑臂展开/收拢过程中所需外力矩的表达式。

6.2 仿真分析

图8 展开过程外力矩的变化Fig.8 Variety of torsion during deploying

用ADAMS对单元段的展开和收拢过程进行了仿真。考虑到拉索的柔性，本文用BUSHING元相连的多段刚体来模拟拉索。在模型中通过传感器(SENSOR)实现了拉索的锁定。对试验件[8]单元段进行了“解锁—收拢—展开—锁定”的动力学仿真，外力矩变化如图8所示。

由图8可知解锁瞬间Me=-175.7 Nm，锁定瞬间Mu=125.4 Nm，与式(15)和(16)的理论值进行对比，如表1所示。由表1可知仿真结果与理论结果误差为2.8%，两者数据吻合。

为验证理论计算与仿真的正确性，对支撑臂单元段展开过程和收拢过程所需的外力矩进行了试验。对试验件进行3次收拢和展开试验，测试结果见表2。

表1 不同方法获得的外力矩比较

表2 最大外力矩的试验结果

7 结束语

本文针对试验件[8]进行了分析，获得如下结论：

1)球铰接杆式支撑臂的剪切刚度由斜拉索的弹性模量、横截面面积和斜拉索倾角决定；扭转刚度与剪切刚度成正比，比例系数为横杆长度s的平方。在s=0.8 m情况下，为获得最佳的剪切刚度与扭转刚度，斜拉索倾角β的最佳取值范围为29.7°～40.4°。

2)球铰接杆式支撑臂中单元段的一阶弯曲频率先随着斜拉索预张力的增加而增加，当一阶弯曲频率达到最大值后，预张力继续增加，一阶弯曲频率反而降低。试验件的最佳预张力范围为500～700 N。

3)球铰接杆支撑臂锁定瞬间所需外力矩由锁定力、横杆长度及斜拉索倾角决定,关系如式(15)所示；解锁瞬间所需外力矩如式(16)所示。

4)支撑臂锁定和解锁瞬间外力矩的仿真结果、理论计算结果与试验结果的误差在3%以内，证明了理论推导和仿真的正确性。

[1] SIDWELL, VINCE. Stiffening of the ACES deployable space boom [R]. NASA-95N26307, 1995.

[2] ADAMS L R. Design, development and fabrication of a deployable retractable truss beam model for large space structures application[R]. NASA-CR-178287, 1987.

[3] YUKI MICHII, ART PALISOC, BILLY DERBES, et al. Truss beam with tendon diagonals-mechanics and designs[C].47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference,Rhode Island,Newport,2006.

[4] 郭宏伟, 刘荣强, 邓宗全. 柔性索对空间索杆铰接式伸展臂性能影响分析[J]. 哈尔滨工业大学学报, 2010, 42(1):55-59.

GUO HONGWEI, LIU RONGQIANG, DENG ZONGQUAN.Influence of flexible cable on performance of space cable-strut deployable articulated mast [J]. Journal of Harbin Institute of Technology, 2010, 42(1):55-59.

[5] 苏斌, 关富玲, 石卫华, 等. 索杆式伸展臂的结构设计与分析[J]. 工程设计学报, 2003, 10(5): 287-294.

SU BIN, GUAN FULING, SHI WEIHUA, et al. Design and analysis of rod-cable deployable mast[J]. Journal of Engineering Design, 2003, 10(5): 287-294.

[6] 郭宏伟, 刘荣强, 邓宗全, 等. 空间索杆式伸展臂展开过程力学分析与仿真[J]. 机械设计, 2008, 25(7): 31-35.

GUO HONGWEI, LIU RONGQIANG, DENG ZONGQUAN, et al. Mechanics analysis and simulation on the spreading process of space cable-rod typed stretching arm [J]. Journal of Machine Design, 2008, 25(7):31-35.

[7] 刘志全, 黎彪, 丁锋. 球铰接杆式支撑臂展开过程中横向振动分析[J]. 宇航学报, 2014,35(7): 753-761.

LIU ZHIQUAN, LI BIAO, DING FENG. Analysis of transverse vibration of an ADAM-Type mast in deployment process [J]. Journal of Astronautics, 2014, 35(7):753-761.

[8] 黎彪，刘志全，程刚，等. 球铰接杆式支撑臂构型参数分析[J].中国空间科学技术, 2012, 32(2):29-34.

LI BIAO, LIU ZHIQUAN, CHENG GANG, et al. Configuration parameter analysis for ADAM-type articulated mast[J]. Chinese Space Science and Technology, 2012,32(2):29-34.

[9] LIU C S, ZHANG K, YANG R. The FEM analysis and approximate model for cylindrical joints with clearances[J]. Mechanism and Machine Theory,2007, 42: 183-197.

(编辑：杨婵)

Influence of Structural and Mechanical Parameters in Diagonal Component on the Performance of ADAM-type Articulated Mast

LI Biao LIU Zhiquan CHENG Gang DING Feng

(China Academy of Space Technology, Beijing 100094)

The influence of the diagonal structural parameter (the angle between the diagonal cable and the batten) on the mast shear stiffness and the torsion stiffness was analyzed. An optimization range of the angle was obtained to determine the batten length. The minimum and maximum value of preloads of diagonal cables were obtained based on the rules that the loads on rods would be less than the allowable buckling stress and the mast wouldn′t collapse on orbit. The relationship between the preloads of diagonal cables and contact stiffness of spherical joint was obtained by the Hertz contact theory and the Winkler beam base hypothesis. Afterward, considering the relationship, the modal analysis was carried out with a finite element model of a mast bay. The analysis results show that the fundamental frequency would increase as the preload increases first, and then the frequency would decrease. Also, the optimization range of preloads in test model is between 500 to 700 N. The relationship between the maximum torsion during deploying/retracting and latch/unlatch force was obtained by static analysis and ADAMS simulation, the results of static analysis and ADAMS simulation is consistent. Then the maximum torsion test during deploying/retracting was carried out. By comparing with the test data, the error of the static analysis results and the ADAMS simulation one is less than 3%.

ADAM-type articulated mast; Diagonal cable; Preload; Latch force; Unlatch force

2014-12-24。收修改日期：2015-01-08

10.3780/j.issn.1000-758X.2015.02.005

黎 彪 1985年生，2013年获中国空间技术研究院飞行器设计专业博士学位，工程师。研究方向为航天器机构设计与分析。