“北斗”导航卫星定轨残差特征提取与分布检验

陈略 唐歌实 崔红正 陈明 刘荟萃 王美

(1 北京航天飞行控制中心，北京 100094) (2 航天飞行动力学技术国家级重点实验室，北京 100094)

“北斗”导航卫星定轨残差特征提取与分布检验

陈略1,2唐歌实1,2崔红正1,2陈明1,2刘荟萃1,2王美1,2

(1 北京航天飞行控制中心，北京 100094) (2 航天飞行动力学技术国家级重点实验室，北京 100094)

针对“北斗”导航卫星定轨残差中非建模系统误差问题，提出基于总体平均经验模式分解(EEMD)与Hilbert谱分析相结合的定轨残差特征提取方法，并对定轨残差正态分布特性进行卡方检验。首先，分析总体经验模式分解原理，提出滤波辅助的改进EEMD方法与Hilbert谱特征提取结合，建立定轨残差特征提取模型，并阐述卡方检验正态分布原理；然后对北斗导航卫星伪距与载波相位数据定轨残差特征进行分析；最后将提出的方法应用于多测站、多北斗GEO卫星的定轨残差分析中。结果表明，EEMD与Hilbert谱方法有效提取出了定轨残差中1天的轨道周期项，且EEMD处理后定轨残差的卡方统计量为5.5，其值小于卡方检验临界，可视为正态分布。该方法可为北斗定轨残差中非建模系统误差分离、提高定轨内符合精度提供有效技术手段。

定轨残差；特征提取；分布检验；伪距；载波相位；总体平均经验模式分解；北斗导航卫星系统

1 引言

“北斗”卫星的观测量包括伪距观测量与载波相位观测量，利用伪距观测量、载波相位观测量可对“北斗”导航卫星进行高精度定轨。定轨残差是定轨内符合精度表现形式之一，通过检测定轨残差可评估定轨精度[1]。提高卫星星历、钟差及相关模型参数的精度，进而提高卫星精密定轨精度，是提高北斗卫星导航系统精密定位服务能力的关键[2]。影响北斗定轨解算的非建模系统误差产生的原因很多，包括多路径影响、卫星轨道、电离层延迟、对流层延迟及卫星钟差等。通常电离层、对流层、卫星钟差等误差可通过建模进行误差修正，但对于某些难以模型化的误差则通常简单地忽略其影响，这些非建模系统误差成为高精度北斗定轨的主要误差源之一，且在定轨残差中普遍存在。如果能对“北斗”卫星的定轨残差进行特征提取，找出其隐藏信息，对于“北斗”定轨残差中非建模系统误差分离与建模具有重要意义。

本文研究将总体平均经验模式分解(EEMD)方法引入到定轨残差分析中，提出滤波辅助的改进EEMD方法，用于精确提取“北斗”定轨残差中的特征量。EEMD方法来源于经验模式分解(EMD)[3]，已被迅速成功应用于雷达信号处理、遥感数据处理、生物信号处理、心电信号处理、故障诊断和表面肌电信号处理等领域[4-5]。

针对“北斗”导航卫星定轨残差分析这一研究问题，本文提出利用EEMD与Hilbert谱的北斗定轨残差非系统建模误差特征提取方法，用于精确提取“北斗”定轨残差中的特征信息，并通过卡方检验方法来对定轨残差的分布特性进行定量检验，以期后续能对“北斗”定轨残差中非建模系统误差进行准确分离建模，旨在提高对“北斗”导航卫星的精密定轨精度。

2 定轨残差特征提取

“北斗”定轨残差是指针对“北斗”导航卫星的观测值减去观测量的计算值，定轨残差直接反应了对卫星定轨的内符合精度。定轨残差表征是一个时间序列，可看成一个时间序列的信号，因此可以利用时间序列分析方法去分析定轨残差。而卡方检验是检验时间序列是否呈正态分布的有效方法。下面介绍“北斗”定轨残差特征提取与残差分布检验基本理论。

2.1 EEMD分解

EEMD分解的原理步骤[4]如下：首先，通过对信号多次加入具有均匀尺度、幅值标准差为常数的随机高斯白噪声序列后，使原信号具有足够的极值点。然后，对每次加入高斯白噪声后的信号进行EMD分解得到相应基本模式分量(IMF)，利用不相关随机序列的统计均值为零的原理，将所有对应的IMF做总体平均运算，消除了多次加入的高斯白噪声对真实IMF的影响。最后将总体平均后的IMF作为EEMD分解的IMF最终结果，这就是EEMD分解方法[7]。EEMD分解方法有效避免了EMD方法中模式混淆现象。

在EEMD分解方法中，加入的白噪声(σ)与总体平均次数(N)是两个最重要参数。加入的高斯白噪声应既不影响信号中的有效高频成分极值点间隔的分布特性，同时又能改变信号中低频成分的极值点间隔的分布特性[5]。文献[4]提出EEMD方法中加入高斯白噪声准则：

(1)

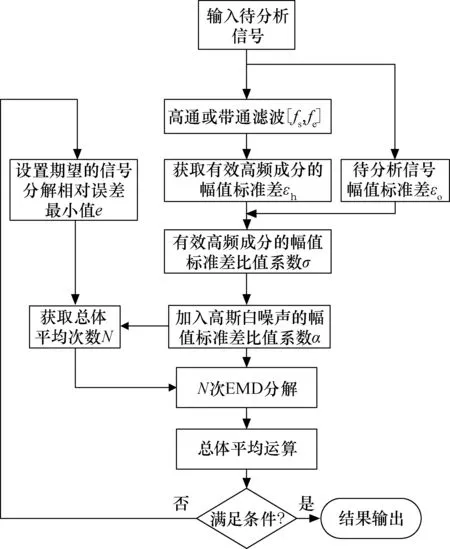
图1 滤波辅助的改进EEMD算法流程Fig.1 Algorithm flow chat of improved EEMD with filter assisting

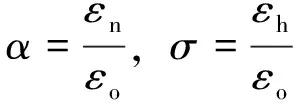
为更有效地确定σ值，本文提出通过滤波方式来确定σ值，即首先对原始分析信号进行高通或带通滤波，评估指定频带内的信号分布特性，确定εh值，得到σ值，进而确定α值。滤波器通带频率选取可根据分析信号特征确定，例如通带选择可采用[3fs/8,fs/2]，即包含分析信号的高频段成分，fs为采样频率。这样就得到一种滤波辅助的改进EEMD方法，其算法流程如图1所示。

2.2 Hilbert包络谱

图2 “北斗”定轨残差特征提取方法模型Fig.2 Feature extraction flow chart of COMPASS orbit residuals

Hilbert变换的定义[8]为

(2)

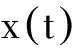
基于以上原理，本文提出了总体平均经验模式分解与Hilbert谱的北斗定轨残差非系统建模误差特征提取方法，其处理流程如图2所示。

2.3 卡方检验正态分布原理

卡方统计量计算公式为

(3)

式中Ai为i水平的观测频数；Ei为i水平的期望频数；n为总频数；pi为i水平的期望频率；k为单元格数。i水平的期望频数Ei等于总频数n×i水平的期望概率pi。

由卡方统计量计算公式可知，当观察频数与期望频数完全一致时，χ2值为0；观察频数与期望频数越接近，两者之间的差异越小，χ2值越小；反之，观察频数与期望频数差别越大，两者之间的差异越大，χ2值越大。在进行卡方正态分布检验时，其方法为：将计算χ2值与理论χ2临界值进行比较，如果计算χ2值小于理论χ2临界值，则接受无效假设H0，反之，拒绝无效假设H0。理论χ2临界值可通过查卡方检验临界值表所得。

3 定轨残差特征分析

从以上伪距残差与载波相位残差中可以看出，CUT0-CO1伪距残差波形较为杂乱，含有大量随机噪声，但仔细分析可以看出较模糊的周期调制信息，CUT0-CO1载波相位残差波形杂乱，含有大量随机噪声，未直观地观测出明显特征。GSMD-CO3伪码定轨残差中还有大量随机噪声，但波形为均匀分布，GSMD-CO3载波相位定轨残差较杂乱，但能看见三个明显的下降峰值。因此，可以看出在北斗定轨残差中，包含了丰富的信息，从波形分布可以看出定轨残差并没有呈现出理想情况下的随机分布，因此可以推断在北斗的定轨残差中包含了可以提取的特征信息，如果能提取这些信息，就能对定轨残差中的非建模系统误差进行提取与分离，有望提高北斗卫星定轨的内符合精度。

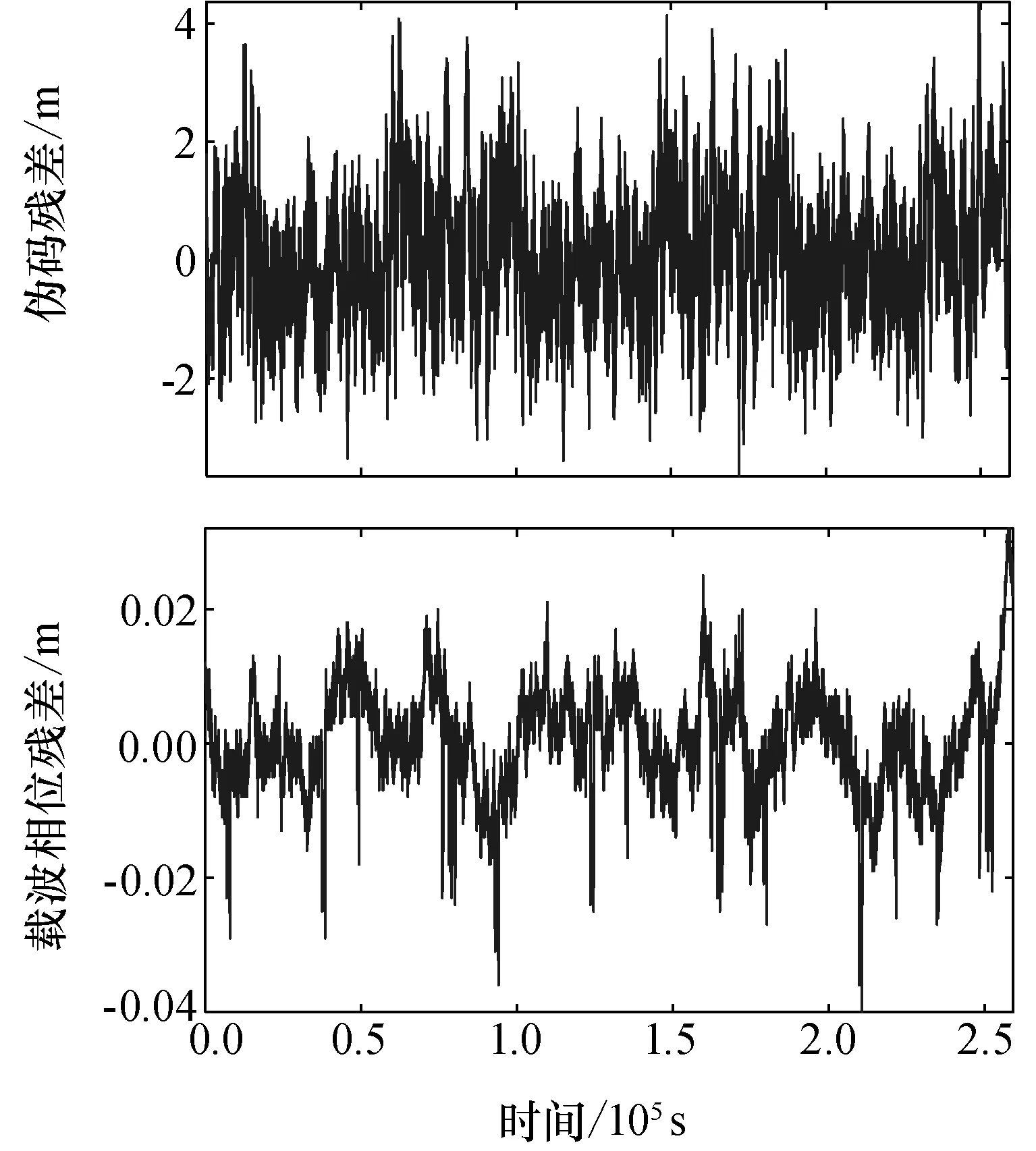
图3 CUT0-CO1伪距与载波相位定轨残差Fig.3 Pseudo-range and carrier phase orbit determination residuals of CUT0-CO1

图4 GSMD-CO3伪距与载波相位定轨残差Fig.4 Pseudo-range and carrier phase orbit determination residuals of GSMD-CO3

4 实例分析

下面通过一个CUT0-C01的载波相位定轨残差数据为例，分析提取定轨残差中特征信息，然后给出不同接收站针对不同“北斗”GEO卫星定轨残差中的特征提取结果。

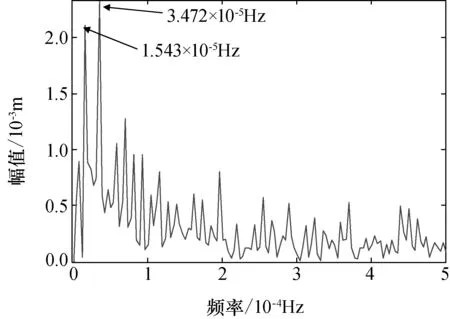
图5 CUT0-C01载波相位定轨残差的频谱分析Fig.5 FFT spectrum of carrier phase orbit determination residuals of CUT0-C01

如第3节所述，CUT0接收站接收C01“北斗”导航卫星的载波相位定轨残差如图3所示，对其进行最常用的傅里叶频谱分析，其频谱如图5所示。在图5中，发现了两个主要的峰值频率，分别为1.543×10-5Hz(显示时，四舍五入到小数点后3位)与3.472×10-5Hz，对应的周期分别为64 809 s与28 802 s。考虑定轨残差的物理意义及GEO卫星运动规律，并不能直接得出这两个频率的物理含义。由于传统频谱分析是基于傅里叶变换，而傅里叶变换是建立在数据平稳性假设条件下的一种频域全局性变换，对于分析平稳与准平稳时间序列十分有效，但对分析非平稳时间序列的能力有限，不能很好揭示非平稳时间序列的特征[4]，因此需进一步进行“北斗”定轨残差数据分析。

运用本文提出的总体平均经验模式分解与Hilbert包络谱方法对CUT0-C01载波相位残差进行分析。滤波通带设置为[3fs/8，fs/2]，滤波器选取为FIR滤波器，期望的信号分解相对误差最小值e设置为0.002，因此得到EEMD分解方法中的加入白噪声大小系数为0.026 4，总体平均的次数为174。其中得到8个IMF，和一个残余项。图6、图7是对定轨残差序列进行EEMD分解后所得的IMF。其中，“signal”表示原始载波相位残差，“C1”、“C2”、…、“C8”分别为第1至第8个IMF，“r”表示剩余项。可以看出，原始载波相位残差按照频带高低被自动分解为8个IMF和1个剩余项，在此过程中，原始载波相位残差中的特征信息分别落入8个IMF中。为进一步精确提取这些特征信息，对所得IMF进行谱分析。

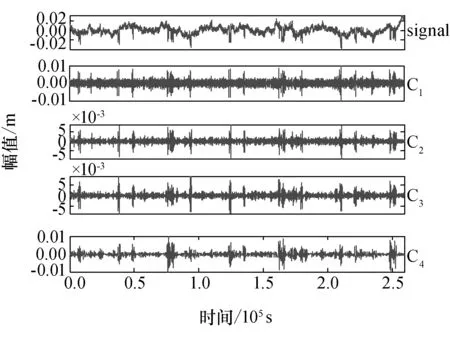
图6 CUT0-C01载波相位定轨残差EEMD分解1Fig.6 1th EEMD results of carrier phase orbit determination residuals of CUT0-C01

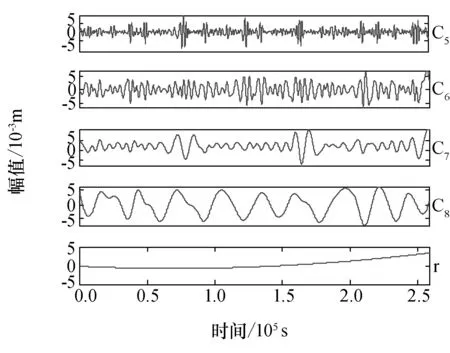
图7 CUT0-C01载波相位定轨残差EEMD分解2Fig.7 2nd EEMD results of carrier phase orbit determination residuals of CUT0-C01

将EEMD分解后所得的IMF进行Hilbert包络谱分析，其结果分别如图8、图9所示，分别对应第1个IMF至第8个IMF的Hilbert包络谱。从图8中明显可以找出峰值频率2.315×10-5Hz；6.944×10-5Hz，从图9中明显可以找出峰值频率1.157×10-5Hz，2.315×10-5Hz，3.472×10-5Hz。

图8 CUT0-C01定轨残差EEMD分解后的Hilbert谱1Fig.8 1 th Hilbert spectrum of orbit determination of EEMD results in CUT0-C01

图9 CUT0-C01定轨残差EEMD分解后的Hilbert谱2Fig.9 2nd Hilbert spectrum of orbit determination of EEMD results in CUT0-C01

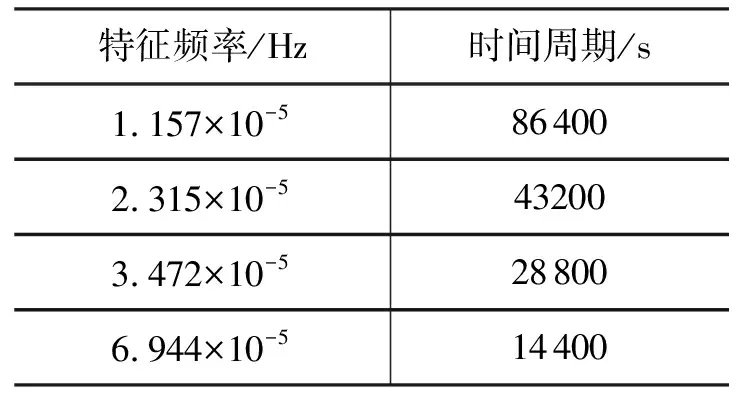
表1 特征频率与周期对照表

在图8中1.517×10-5Hz在四舍五入前的真实频率为1.517 407 407 5×10-5Hz。将特征频率转换为时间周期如表1所示。从表1中可以看出，在Hilbert包络谱中的峰值频率1.517×10-5Hz严格对应86 400 s，正好是1天的积秒。其余峰值特征频率是1.157×10-5Hz的2,3,6倍频。因此，初步判定在CUT0-C01的载波相位定轨残差中存在一个与1天相关的时间周期项，结合“北斗”GEO卫星的轨道运行规律，推断定轨残差中可能包含与轨道运动周期严格对应的特征信息。

为进一步验证以上推论，选取CUT0/GSMD/JFNG接收站对多颗“北斗”GEO卫星的定轨残差运用本文提出的特征提取方法进行分析，找出其中最明显的两个特征频率，其统计结果如表2所示。C01、C03、C04、C05均为北斗GEO卫星。表2中，“/”表示在Hilbert包络谱中仅存在1个最明显频率成分，其他频率成分相对较弱。从表2中可以看出，在CUT0、GSMD、JFNG站针对多颗北斗GEO卫星的定轨残差中，均存在与轨道运动周期1天相对应的时间项，表现为存在基频1.157×10-5Hz以及1.157×10-5Hz的倍频。初步判断产生此现象可能的原因为“北斗”导航卫星运动受到太阳光压的影响产生了周期成分，抑或是“北斗”导航卫星信号从发射到接收过程中经过了较为复杂的传播路径，如多径效应[8]等影响，在接收机端接收到的信号相互调制，产生非线性耦合现象，非线性的主要表现为不同信号频率成分间的调制现象，产生了频率边带结构。从以上分析可看出，基于总体平均经验模式分解与Hilbert谱的定轨残差特征提取方法比传统傅里叶变换更能准确提取淹没在噪声中的特征信息。

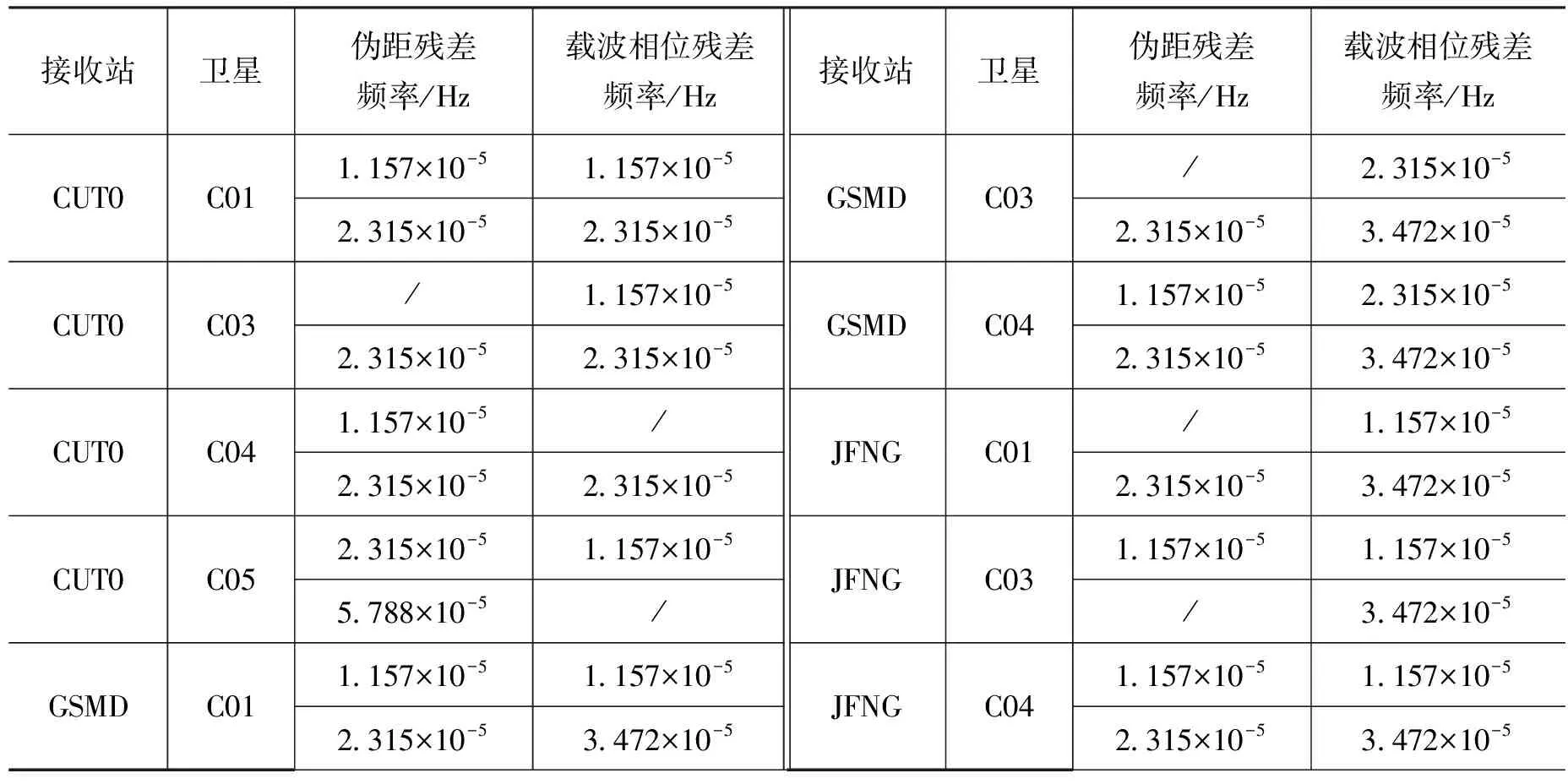
表2 定轨残差中最明显的频率特征

图10 CUT0-C01伪距定轨残差分解为模型信号与剩余项信号Fig.10 Model signal and residuals signal of Pseudo-range orbit determination residuals of CUT0-CO1

为进一步说明总体平均经验模式分解方法在处理定轨残差数据中的有效性，利用卡方检验分析处理前后北斗定轨数据的分布特性。以CUT0-C01的伪距定轨残差数据的EEMD分析为例，通过EEMD分解与重构后，可将CUT0-C01信号分解为一个模型信号与剩余项信号，如图10所示，模型信号由EEMD分解中的中低频信号组成，剩余项信号由EEMD分解中的高频信号组成。

分别对CUT0-C01定轨残差原始信号与剩余项信号进行卡方检验正态分布分析。卡方检验的统计自由度为7，显著性水平为0.05。原始信号所得χ2=157.616 5，剩余项信号所得χ2=5.505 6。经查卡方检验临界值表，对应自由度与显著性水平的χ2临界值为14.067 1。因此，运用卡方检验方法不难得出，原始信号H0=1，即原始信号不满足正态分布；剩余项信号H0=0，即剩余项信号满足正态分布。剩余信号成正态分布，满足理想定轨残差的分布特性，推断定轨残差中的有效信息主要存在于模型信号中，因此通过卡方检验进一步验证了EEMD方法可有效分离出定轨残差中包含的特征信息。

5 结束语

1)本文提出了总体平均经验模式分解与Hilbert谱相结合的“北斗”定轨残差特征提取方法，准确提取“北斗”导航GEO卫星的非建模系统误差的特征信息，相比传统傅里叶频谱分析方法，在准确提取“北斗”定轨残差特征信息中具有更高的可靠性和灵敏度。

2)在“北斗”导航卫星的伪距与载波相位的定轨残差中，存在与轨道运动天周期(86 400 s)相关的特征频率1.157×10-5Hz及其倍频。

3)卡方检验验证了总体平均经验模式分解方法在定轨残差分析中的有效性。

4)后续需进一步开展的工作包括，一是深入研究“北斗”导航卫星定轨残差中产生不同周期项的原因，二是对提取出的特征频率定量信息在定轨残差中重新建模，去除此项非建模系统误差，并通过定轨试验来验证建模的准确性与可靠性。

致谢

感谢CUT0、GSMD、JFNG等GNSS卫星国际接收站提供的北斗导航卫星的伪距与载波相位观测量数据。

[1] 郭向, 张强, 赵齐乐, 等.基于单频星载GPS数据的低轨卫星精密定轨[J]. 中国空间科学技术，2013,33(2):41-46.

GUO XIANG, ZHANG QIANG, ZHAO QILE，et al. Precise orbit determination for LEO satellites using single-frequency GPS observations [J].Chinese Space Science and Technology, 2013, 33(2):41-46.

[2] 施闯, 赵齐乐, 李敏, 等.北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学：地球科学, 2012, 42(6): 854-861.

SHI CHUANG,ZHAO QILE, LI MIN, et al. Precise orbit determination of Beidou satellites with precise positioning [J]. Science China Earth Science., 2012, 42(6)：854-861.

[3] HUANG NORDEN E, ZHENG SHEN, STEVEN R L. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc. R. Soc. Lond. A, 1998, 454：903-995.

[4] 陈略, 訾艳阳, 何正嘉, 等.总体平均经验模式分解与1.5维谱的方法研究[J].西安交通大学学报, 2009, 43(5):94-98.

CHEN LUE, ZI YANYANG, HE ZHENGJIA, et al. Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method [J]. Journal of Xi′an Jiaotong University, 2009, 43(5): 94-98.

[5] CHEN LUE, ZI YANYANG, HE ZHENGJIA, et al. Rotating machinery fault detection based on improved ensemble empirical mode decomposition [J]. Advances in Adaptive Data Analysis, 2014, 6(2):1-24.

[6] WU ZHAOHUA, HUANG NORDEN E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1):1-41.

[7] 何正嘉,訾艳阳,张西宁.现代信号处理技术及应用[M].西安：西安交通大学出版社，2007:61-62.

[8] LIU HUICUI, LI XIAOJING, GE LINLIN, et al. Variable length LMS adaptive filter for pseudorange multipath mitigation [J]. GPS Solutions, 2011, 15(1): 29-38.

(编辑：车晓玲)

Feature Extraction and Distribution Test for Orbit Residuals in Beidou Navigation Satellite

CHEN Lue1,2TANG Geshi1,2CUI Hongzheng1,2CHEN Ming1,2LIU Huicui1,2WANG Mei1,2

(1 Beijing Aerospace Control Center, Beijing 100094)

(2 National Key Laboratory of Science and Technology on Aerospace Flight Dynamic, Beijing 100094)

To analyze the no-modeling system error of orbit residuals in COMPASS, the orbit residuals feature extraction method with the ensemble empirical mode decomposition (EEMD) and Hilbert spectrum was proposed, and the normal distribution character of the orbit residuals chi-square test was analyzed. Firstly, the feature extraction principle of EEMD and Hilbert spectrum was introduced,the EEMD method assisted by the filter was proposed, and the feature extraction model of orbit residuals was established. Secondly, the feature of Pseudo-range and carrier phase orbit residuals in COMPASS was analyzed. Finally, the EEMD and Hilbert spectrum method was applied to analyze the Beidou GEO satellite orbit residuals. The results show that EEMD and Hilbert method can accurately extract the features of 1 day period, which is related to Beidou orbit running period. The chi-square value of the post orbit residuals obtained by EEMD is 5.5, which is smaller than the critical value of chi-square test. It proves that the post orbit residuals are normal distribution. The proposed method is important for separating the no-modeling system error in Beidou navigation satellite orbit residuals to improve the orbit determination precision.

Orbit residuals；Feature extraction；Distribution test；Pseudo-range；Carrier phase；Ensemble empirical mode decomposition；COMPASS

国家自然科学基金(41304026)资助项目

2014-07-11。收修改稿日期：2014-11-06

10.3780/j.issn.1000-758X.2015.02.001

陈 略 1983年生，2009年获西安交通大学机械工程及自动化专业硕士学位，工程师。研究方向为无线电测量与科学应用、地球自转参数解算与预报。