加速度计整流误差校准方法*

董雪明 何懿才 马博禹 秦朝俊 杨海龙 刘静雅

(中航工业北京长城计量测试技术研究所，北京100095)



加速度计整流误差校准方法*

董雪明 何懿才 马博禹 秦朝俊 杨海龙 刘静雅

(中航工业北京长城计量测试技术研究所，北京100095)

整流误差是衡量外部振动对加速度计性能影响的重要指标。传统的整流误差校准方法，采用单方向、纯振动的激励来进行整流误差校准。此类方法难以真实评价振动噪声的影响。通过对传统整流误差校准方法进行研究，本文提出了一种基于多方向复合加速度输入的加速度计整流误差校准方法，有效解决了加速度计整流误差的校准。

加速度计；整流误差；振动台；双离心机；复合校准

0 引言

所谓整流误差，是指在直线振动和冲击作用下(有的情况同时还有角振动作用)，加速度输出信号中出现虚假的直流分量，是一种时域的稳态误差。整流误差产生的虚假输出会引起加速度计偏值和标度因数的改变。这两个关键参数的变化将引起整个惯性系统的测量误差。特别是新兴的MEMS电容式加速度计、科里奥利速率陀螺以及闭环的电容式测力仪，其整流误差特性都很差。比如，一种已知的静电梳齿结构MEMS电容式加速度计,在输入轴输入幅度为10g的振动时，对该加速度计的平均输出的改变速率高达0.1g/s，因此，此类加速度计是不适合当前的战术级和导航级应用的。由于整流误差随加速度计以及载体外部环境而变化，难以通过硬件手段直接补偿，所以，有必要对整流误差进行校准，获取其变化规律以进行补偿。

当前大多数加速度计整流误差的研究，都是针对特定类型的加速度计，从加速度计设计、制造出发，改进加速度计性能，从根本上隔离或消除外部影响；而通过测试、校准手段获取振动干扰规律并补偿整流误差的研究并不多见。一方面是因为实际应用中整流误差的来源复杂，很难确切把握振动干扰的确切规律；另一方面是缺少有关整流误差测试、校准的通用方法和装置，以及定量评价的可行方案。

1 传统的整流误差校准方法

整流误差产生的原因是复杂的，不同类型的加速度计的整流误差来源也不一致。就某些摆式加速度计而言，由于是依赖加速度计内部机械结构产生的位移变化、应力变化或力矩变化等实现加速度测量的，外部振动则会引入对这些变化的干扰，即由所谓的振摆特性和非等弹性引起；对MEMS电容式加速度计，则可能有非线性的再平衡力、标度因数的不对称性、再平衡力与等效质量中心的耦合性及阻尼液影响ECM位置等。

一般的整流误差校准方法，是从整流误差的定义出发，给加速度计输入零均值的振动，记录加速度输出的直流量变化，然后除以输入振动幅度的均方根的平方，得到一个“整流误差因子”。施加的零均值振动可以是单频率的正弦振动，也可以是连续施加的多个正弦振动，或者是规定好的随机振动谱。

为给加速度计输入标准的振动信号，目前采用的手段主要有两类：第一类是基于电流/电压激励的方法(内部激励法)，即在详细了解加速度计结构的基础上，通过给加速度计电路直接输入电压或者电流进行激励，测量其整流误差；第二类是基于机械振动的方法(外部激励法)，即将被测加速度计作为整体考虑，通过标准装置产生所需的振动激励(正弦激励或者随机振动谱)输入到被测加速度计，测量其整流误差。第一类方法直接对加速度计电路进行操作，只适合于研发设计人员使用，对于应用工程师和一般用户，是无法使用的。因此，主要用在加速度计设计研发阶段，如结构改进、参数调整等场合；第二类方法把加速度计当作一个“黑盒”，直接作为整体进行测试。这一类方法是绝大多数加速度计使用者采用的方法。

目前的整流误差定义及测试方法主要是把这一特性当作加速度计的物理结构特性的表征，考虑的是单一振动在单方向输入情况下的加速度计输出当中直流量的变化。但是，单一振动是一种理想的状态，在实际情况中很难出现。

第一，在实际工作环境下，振动干扰是与理想输入混合在一起，同时激励加速度计。将理想输入与振动干扰分离，单独考虑振动干扰对加速度计的影响，不能全面衡量振动干扰导致的误差。第二，振动干扰一般具有多源性。由于加速度计的安装，以及振动源的来源不同，最终施加在加速度计上的振动干扰常常是来自多个方向。仅仅考虑输入轴方向的振动干扰，不能够充分评价振动的影响。

因此，针对整流误差的研究，目前采用单方向的振动测试是不能充分评价整流误差在实际过程中的影响的，有必要结合实际情况，提出基于理想输入与振动干扰同时激励、多方向输入的研究，即开展基于复合加速度的加速度计整流误差校准。

2 现状及发展趋势

实际测试计量工作中，对整流误差的测试、校准，都是采用振动台作为振动激励，输出单方向正弦振动或随机振动谱进行测试。如前所述，在传感器的应用环境中，振动加速度通常不是单一存在的，而且也不是单方向存在的。最简单的情况是，在同一方向下，作为干扰的振动加速度与作为输入的固定值加速度混合在一起，作为加速度计的输入。这样混合加速度产生的输出特性是与单独的固定值加速度作为输入、或单独的振动加速度作为输入得到的输出特性不一致的。进一步考虑到振动的多源性、多向性。在部件众多、结构复杂的载体上，振动无疑是十分复杂的。最一般的情况是，多方向的振动与多方向的固定值加速度作为干扰，与理想的加速度计输入(可能是振动加速度，也可能是固定值加速度)一起作为加速度计的激励。因此，有必要对整流误差进行进一步的研究。我们提出的新方法，是采用多方向的复合加速度进行校准。传统方法只能模拟理想的情况，不能复现复杂的实际情况；而本文方法能够贴近实际的使用环境，得到的测试结果有助于评估传感器在使用过程当中的性能。

基本研究思路如图1所示。在第2步，含恒加速度与振动加速度分别施加在加速度计的不同轴上的情况。比如，IA(输入轴)输入振动加速度，OA(输出轴)、PA(摆轴)方向施加恒加速度，或者IA输入恒加速度，OA、PA施加振动加速度等。在第4步，除了输入复合加速度的轴以外，其余轴上可能输入振动加速度或者恒加速度的情况。

图1 整流误差校准基本研究思路

要使用复合加速度进行校准，首先要研发可用于产生复合加速度的装置。目前，可产生复合加速度的装置如表1所示。

表1 产生复合加速度的装置

续表

由于离心-振动系统可以产生复杂的复合加速度，通过灵活的配置，能够满足各种需求，因此我们选择使用这种系统结构进行基于复合加速度的整流误差校准。

3 基于单一振动加速度的整流误差校准

产生单一振动加速度的主要设备是振动台。爆炸式振动台使用场合特殊，在整流误差校准中一般不采用；机械式振动台属于早期的振动台类型，在绝大多数场合已被其他类型的振动台替代。在振动测试中，主要使用的是液压式和电磁式振动台。液压式振动台产生频率较低的振动，同时可以产生的振动幅度较大，而电磁式振动台可以产生中高频的振动，同时其振动幅度较小。如果需要对被测对象开展全频率段的完整测试，需要采用多种不同的方法结合使用。

另外，通过双离心机也可以产生振动加速度信号。双离心机原本用于加速度计动态特性的校准，国际标准化组织发布的《ISO 5347-8：1993振动与冲击传感器校准方法第8部分：双离心机法一次校准》及相应的国内标准都有论述。但是，经过研究发现双离心机也是可以用于整流误差校准的。北京长城计量测试技术研究所有一台双离心机，可产生频率0.01～10Hz的零均值正弦加速度，俄罗斯门捷列夫计量院制造的双离心机可产生频率从0.01～30Hz的零均值正弦加速度。不过，双离心机只能够产生正弦振动，无法复现随机振动。而且，双离心机产生的加速度，实际上是2个正交的幅度相等、频率相同、相位相差90°的正弦加速度。因此，在使用双离心机进行整流误差校准时，必须考虑到被测传感器的横向灵敏度是足够低的，横向输出是不影响整流误差结果的。

多振动台的输入方式在横向灵敏度测试当中已经出现。在标准ISO 16063-31:2009中有详细的介绍，比如共振棒、双振动台和三振动台。德国物理技术研究院拥有一台三轴振动的复合振动装置，如图2所示。由三台独立的振动台组成，可以同时沿着加速度计的三个敏感轴方向上输入幅度、频率、相位各异的振动加速度。

这一点双离心机无法实现。双离心机产生的只能是幅度、频率相同，相位相差90°的两个正弦信号。与双离心机产生的加速度相似，倾斜轴转台也能产生两个幅度、频率相同，相位相差90°的两个正弦信号，但其幅度不是连续可调的，而且最大幅度小于1g。

图2 三振动台测试装置

4 基于复合加速度的整流误差校准

使用不同种类加速度的组合对加速度计进行校准，在国内外尚未见到类似的研究报道。我们首次提出使用这种方法进行加速度计的校准，是以多参数环境试验为基础，提升环境试验的测量精度，保证环境试验的参数溯源，从而提出基于多参数复合的加速度计校准。通过使用包含固定值加速度和振动加速度的复合加速度进行校准，是一项基础性的工作。

因此，我们提出使用振动-离心机来产生复合加速度。振动-离心机是用于环境试验的大型设备，一般采用旋臂式离心机与电磁振动台构成。这是一种复杂的系统，通常是将振动台固定在离心机上。振动台的安装方式，主要分为垂臂安装和顺臂安装两种。垂臂安装是指振动台振动方向与离心机旋转平面垂直，顺臂安装是指振动台振动方向与离心机旋转平面平行。根据振动台动圈台面是否朝向旋转中心，顺臂安装方式又可以分为：顺臂朝内和顺臂朝外两种情况。这两种情况下，动圈受力方向是相反的。

图3是振动台顺臂朝内安装方式示意图。

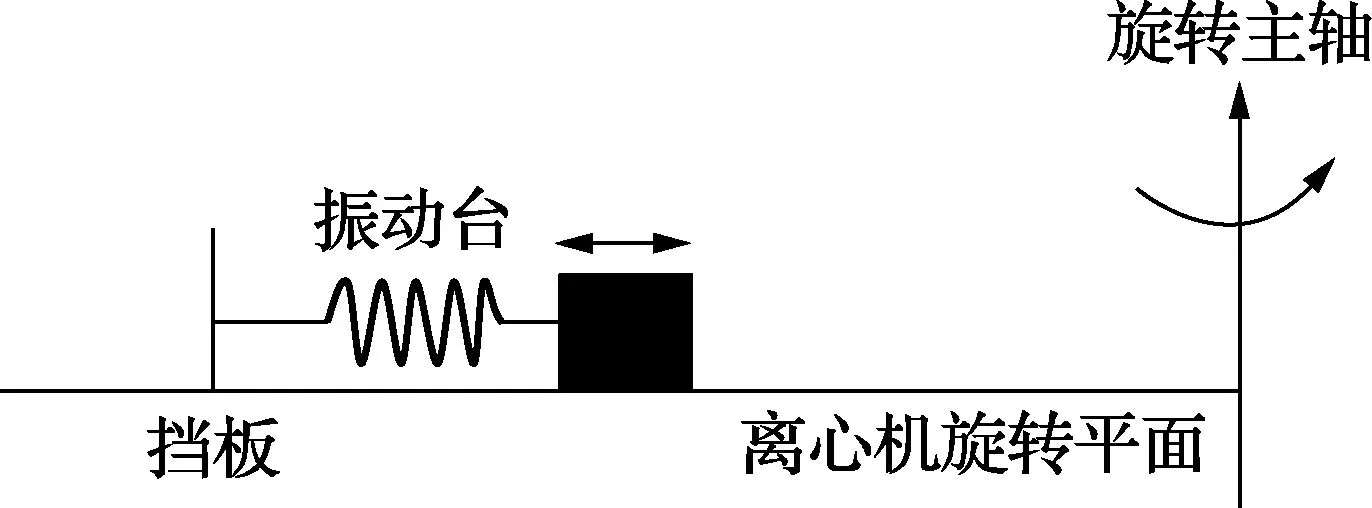
图3 振动台顺臂朝内的安装方式

垂臂安装情况下，向心加速度与振动加速度理论上没有耦合，独立施加在加速度计上。即加速度计受到三个相互独立的加速度输入：来自离心机的向心加速度、来自振动台的振动加速度以及重力加速度。顺臂安装情况下，由于振动台台面及台面上夹具、夹具及加速度计有相对于离心机旋转平面的相对运动，将产生额外的科里奥利加速度，简称“科氏加速度”。科氏加速度矢量与振动加速度矢量、离心机旋转角速度矢量相互垂直。科氏加速度与振动加速度密切联系，与离心机旋转角速度也密切联系。这种情况下，加速度计受到4个加速度输入：来自离心机的向心加速度、来自振动台的振动加速度、由于相对离心机旋转平面运动产生的科氏加速度以及重力加速度。

由此可见，离心-振动系统能够灵活地提供各种复杂的复合加速度，复现接近实际情况的加速度环境。

5 结束语

传统的整流误差校准方法中采用单方向、纯振动的激励方式，不能够充分评估外部振动在加速度实际应用环境下的影响。本文提出的基于多方向复合加速度的加速度计整流误差校准方法，多方向、复合加速度的输入，能够充分校准外部振动对加速度计的影响。

通过构建接近实际应用情况的校准环境，对加速度计进行多参数复合校准，是获得符合加速度计实际工作性能的关键途径。基于多方向复合加速度输入的整流误差校准是其中一个具有开创性的例子，通过此次的研究，为深入探索基于多参数复合校准这一前沿课题提供了很多值得借鉴的研究模式和思路，有重要的参考价值。

[1] IEEEStandard 528-2001,IEEE Standard for Inertial Sensor Terminology, 2001

[2] IEEE Standard 1293TM-1998(R2008), IEEE Standard Specification Format Guide and Test Procedure for Linear, Single-Axis, Nongyroscopic Accelerometers, 2008

[3] IEEE Standard 836-2009, IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers, 2009

[4] ISO 5347-8:1993(E), Methods for the Calibration of Vibration and Shock Pick-Ups-Part 8: Primary Calibration by Dual Centrifuge First Edition,1993

[5] ISO 16063-31, Methods for the calibration of vibration and shock transducers-Part 31: Testing of transverse vibration sensitivity, 2009

[6] Richard Jepsen,Edward Romero.Testing in a Combined Vibration and Acceleration Enviroment[A].Orlando, Florida ,2005

[7] 刘爱东，于梅，马明德.低频振动标准套组的研制[J].计量学报,2010.31(3): 238-240

[8] 乔仁晓，孟晓风，贺忠江，等.精密离心机输出特性建模与误差分析[J].计量学报,2009.30(2): 144-147

[9] Actidyn Systems, V67 Technical Description, http://www.actidyn.com/wp-content/uploads/2010/06/v67.pdf, 2010

[10] Wei Guan, Xueming Dong, Zuhong Long，Accelerometer Transverse Sensitivity Testing with Double Turntable Centrifuge, 2014 IEEE International Instrumentation and Measurement Technology Conference May 12-15, Montevideo, Uruguay, 2014: 578-582

[11] W.Guan, Xueming Dong, Lei Xiong,Calibration of Accelerometer with Multicomponent Inputs, Proc.of 2014 IEEE International Instrumentation and Measurement Technology Conference, May 12-15, Montevideo, Uruguay, 2014: 16-19

[12] Wei Guan, X.M.Dong, Z.H.Long, Lei Xiong, J.Z.Zhao, Evaluation of the accelerometer rectification error by using a double centrifuge, Proc.of 2014 21st Saint Petersburg International Conference on Integrated Navigation Systems, May 26-28, Saint Petersburg, Russia, 2014: 323-327

[13] DONG Xue Ming, GUAN Wei and XIONG Lei, Combined Accelerations Produced by Vibrafuge, Applied Mechanics and Materials Vols.2014:971-974

[14] 董雪明，关伟，何懿才，孙浩，马博禹.基于条件数理论的加速度计校准方案优化[J].计量技术，2014(5):50-52

国防技术基础项目，A类(J052012B001)

10.3969/j.issn.1000-0771.2015.05.05