基于规则产生准则与修剪策略的D-FNN算法研究*

左 军，周 灵，李晓东

(佛山科学技术学院电子与信息工程学院，广东 佛山 528000)



基于规则产生准则与修剪策略的D-FNN算法研究*

左 军，周 灵，李晓东

(佛山科学技术学院电子与信息工程学院，广东 佛山 528000)

提出了一种D-FNN结构及其学习算法，该D-FNN的结构基于径向基神经网络。模糊规则的产生由输出误差或可容纳边界的有效半径决定。修剪技术的应用，使得网络结构能够保持紧凑，学习速度快，确保系统的泛化能力。对所提算法作了详细探讨，并与相关算法作比较，从而发现了D-FNN的独特思想。编写了D-FNN的仿真程序，对具体案例进行了仿真。结果表明，D-FNN具有紧凑的结构和优秀的性能。

动态模糊神经网络；径向基函数；模糊规则；修剪策略

模糊逻辑理论提供了一种数学工具来获取人们认知过程，模糊推理则形式上是利用规则进行推理，其逻辑取值可在0和1之间连续取值，然而不存在正式的框架来选择模糊系统的各种参数。神经网络具有学习能力、自适应能力、并行处理能力以及泛化能力等，具有构建与人们认知有关的各种行为的潜能，但神经网络没有明确的物理意义。把模糊逻辑和神经网络这两种方法结合起来，取各自优点从而构成的动态模糊神经网络，在消费电子、工业控制、系统辨识、模式识别、图像处理等许多领域得到了广泛的应用[1-4]。

1 RBF神经网络与修剪技术理论分析

1.1 模糊神经网络的结构

D-FNN的结构是基于扩展的RBF神经网络。RBF神经网络具有单隐层的三层前馈网络，RBF结构如图1所示。Poggio和Girosi已经证明，RBF网络是连续函数的最佳逼近，它能以任意精度逼近任一连续函数[2]。

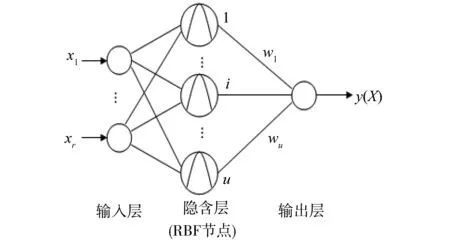
图1 径向基神经网络结构Fig.1 RBF neural network structure

一个具有r个输入和一个输出的RBF神经网络，该网络可以看成如下形式的映射f:Rr→Rs：

(1)

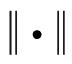
不考虑偏置量，采用高斯函数作为激活函数时，则式(1)可以写为如下的表达式：

(2)

如果高斯函数的输出采用归一化，则径向基网络产生如下归一化输出响应：

(3)

高斯函数不仅适合于全局映射而且适合于细化局部的特征，而且能够达到快速的学习。因此以高斯函数作为激活函数的神经网络称为径向基(RBF)神经网络。由于RBF神经网络具有最好的逼近特性，所以本文的研究是基于动态径向基神经网络[5]。

本文提出了D-FNN结构及其学习算法，该模糊神经网络的结构基于扩展的径向基神经网络。其学习算法能够使结构的辨识和参数的调整同时进行，并且D-FNN能使系统结构小(使用修剪技术)、速度快，可用于实时建模与控制。D-FNN的结构如图2所示，共5层。在图2中，x1,x2,…,xr是输入的语言变量，y是系统的输出，MFij是第i个输入变量的第j个隶属函数，Rj表示第j条模糊规则，Nj是第j个归一化节点，wj是第j个规则的结果参数或者连接权，u指系统总的规则数。

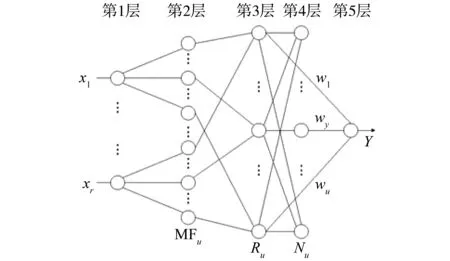
图2 动态模糊神经网络结构Fig.2 D-FNN structure

1.2 规则产生准则理论分析

如果D-FNN规则数太少，系统的性能将表现得很差；规则数太多，增加系统的复杂性，导致系统的泛化能力很差。

误差判断可以表达为：对于第i个观测数据(Xi,ti)，其中，Xi是输入向量，ti是期望的输出，计算D-FNN现有结构的全部输出为yi。

定义

(4)

如果

(5)

需要增加一条新的模糊规则。这里的ke值是根据D-FNN期望的精度预先选定的。

可容纳边界判定可表达为：对于第i个观测数据(Xi,ti)计算输入值Xi和现有RBF单元的中心Cj之间的距离di(j)，即

(6)

其中，u是现有的模糊规则或者RBF单元的数量。

找出

dmin=argmin(di(j))

(7)

如果

(8)

需要增加一条新的模糊规则，否则，观测数据Xi可以由现有的最近的RBF单元表示[6]。这里，kd是可容纳边界的有效半径。

1.3 修剪技术理论分析

修剪技术，即在学习进行时，检测到不活跃的模糊规则并加以剔除，使网络不会持续增长，可获得更为紧凑的D-FNN结构。在本文中我们将采用ERR(误差下降率)方法作为一种为修剪技术来选择重要的模糊规则。这种方法本质上是一种正交变换的方法，其要点是用QR分解把矩阵H变换成一组正交基向量。这个变换使我们可以计算出每一个基向量对期望输出能量值的贡献大小[7]。

假定理想的输出为T=(t1,t2,…,tn)∈Ru，Y为系统的输出。我们的目标是：给定Ψ∈R(r+1)u×n和T∈Rn之间有如下关系[8]：

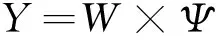
(9)

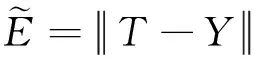
(10)

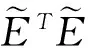
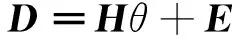
(11)

其中，D=TT∈Rn为期望输出，H=ΨT=(h1…hv)∈Rn×v,v=u×(r+1)称为回归向量，θ=WT∈Rn包含实参数并且假定E∈Rn是与回归量hi不相关的一个误差向量[9]。

对于任意矩阵H，如果它的行数大于列数，通过QR分解：

H=QA

(12)

可把H变换成一组正交基向量Q=(q1,q2,…,qv)∈Rn×v，其维数与H相同，各列向量qi构成正交集，并且A∈Rn×v为一个上三角矩阵。通过这一变换，有可能从每一基向量计算每一个个体对期望输出能量的贡献[3]。

(13)

把新得到的erri(i=1,2,…(r+1)u)重新排列为矩阵Δ=(δ1,δ2,…,δu)∈R(r+1)×u，Δ的第i列δi就是与第i个规则相关的(r+1)个误差下降率。进一步定义

(14)

那么，ηi反映第i个规则的重要性，ηi值越大，表示第i个规则越重要[5]。如果

(15)

其中，kerr表示预设的阈值，则第i个规则可剔除[10]。

2 实验结果与分析

本文将通过Hermite函数逼近以及Mackey-Glass时间序列预测实例来验证D-FNN算法的有效性，并通过D-FNN算法与其他算法的比较，来检验D-FNN在学习效率和性能方面的特点。

一般情况下函数逼近的精度由平方L2-范数来度量，即可以由下式表示

(16)

当一个动态模糊神经网络用于函数逼近问题时，一般形式的表达如下

(17)

其中，wi是权值，Ri(X,wi)是基函数，u是基函数的个数。一旦Ri(X,wi)被选定，权值的选择就可以用线性代数中的标准方法求解。

使用修剪技术与规则产生准则的D-FNN算法仿真实验。被逼近的函数为如下的Hermite多项式

(18)

为了训练学习这个被逼近的函数，使用随机样本函数在区间[-4，4]内来产生200个输入输出数据作为训练集。仿真结果如图3所示。表1列出了用均方根误差表达的结构和性能方面的对比。D-FNN只需要6条规则，就能达到相同的训练误差，比OLS、M-RAN和RANEKF算法所需要的规则数都少[11-13]。由图3(a)、图3(b)可以看出，由于使用了修剪技术，使得D-FNN的结构很小，但其泛化能力很强。仿真结果表明：与OLS、M-RAN和RANEKF算法比较，D-FNN无论在结构上还是性能上都具有明显的优势。

Mackey等人在1977年提出的Mackey-Glass混沌时间序列模型，是用来描述白血病时，血液中白细胞的数量变化情况。许多研究者对这种典型的时间序列预测问题进行了研究。其方程用如下的表达式所示

(19)

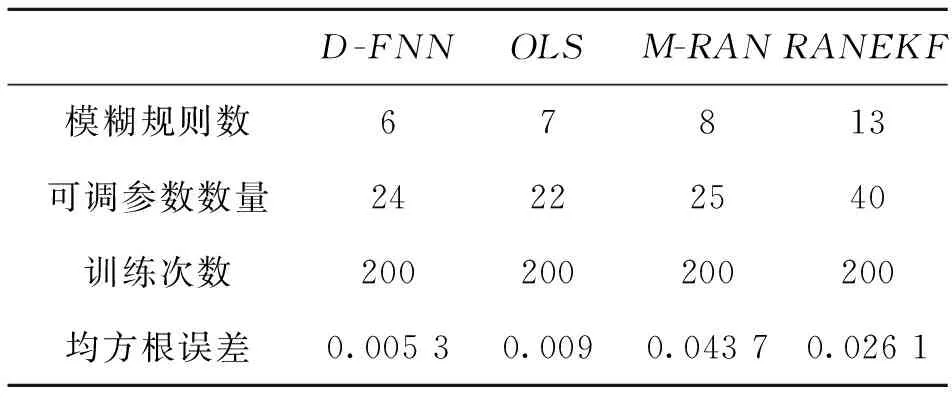
表1 不同算法的均方根误差对比Table 1 RMSE compare different algorithms

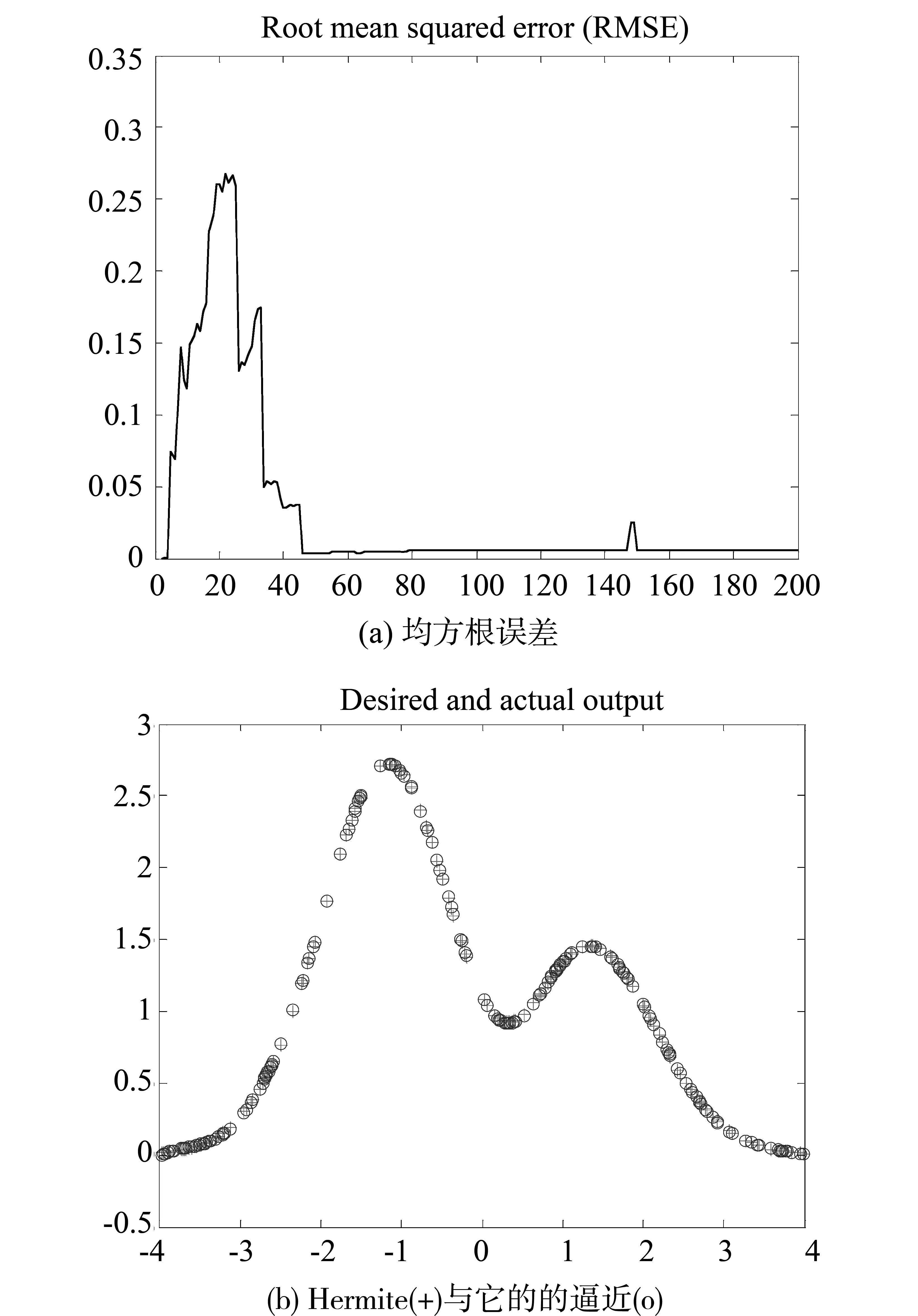
图3 Hermite函数逼近Fig.3 Hermite function approximation

由于新陈代谢生理机制方面的原因，血液中白细胞的数量变化情况在方程(19)中表现出了某种混沌特性与周期性。当τ>17时，方程(19)表现出混沌现象，而当τ<17时，方程(19)表现出周斯性。τ值越大混沌现象越严重。为了能够在相同的基础上进行比较，参数选择为：a=0.1、b=0.2和τ=17。预测模型表示如下：

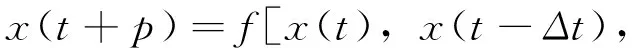
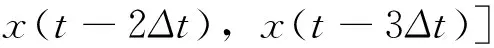
(20)

为了研究训练和测试情况，用方程(19)在t=0到t=6 000之间产生6 000个数据。方程(19)初始条件选为：当t<0时，x(t)=0,x(0)=1.2。6 000个数据将作为输入输出数据来训练预测模型式(20)，使预测模型逼近式(19)，并测试其性能。

设p=6、Δt=6，在111≤t≤610之间随机选择500对数据样本，在111≤t≤1 110之间随机选择1 000对数据样本来作为训练数据。500和1 000个随机样本用来检验被辨识的数据模型。从t=111到t=610的训练结果和前6步预测结果由图4所示。选择参数不同，产生的模糊神经网络结构也不同，其训练均方根误差和测试均方根误差列于表2中。

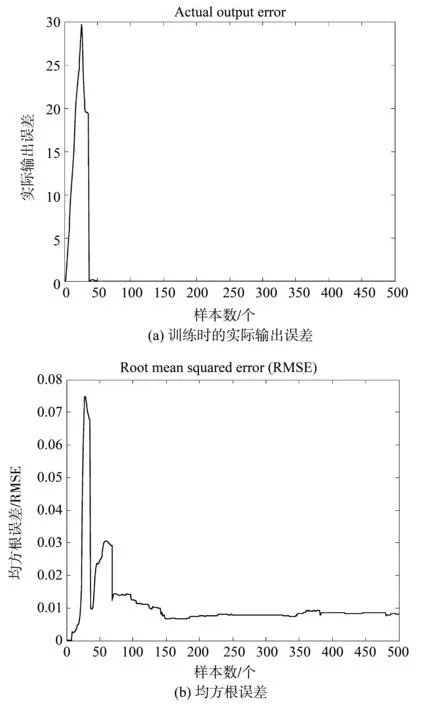
图4 Mackey-Glass时间序列预测Fig.4 Mackey-Glass time series prediction表2 两种不同结构训练和测试仿真结果Table 2 Two different structures for training and testing simulation results

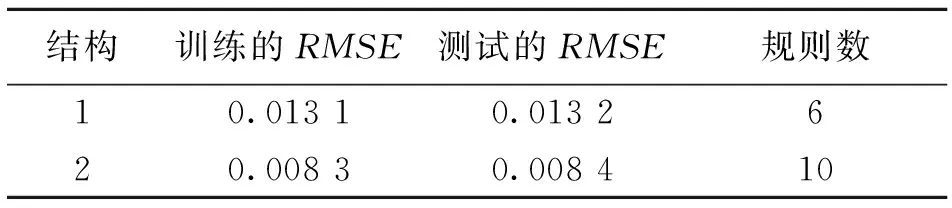
结构训练的RMSE测试的RMSE规则数10.01310.0132620.00830.008410

图5说明了D-FNN泛化性能的测试，其中p=6，D-FNN模糊规则数为10。测试时，采用前500数据样本用于训练模型，后500数据样本用于预测模型。由表2可以看出，因为模型测试误差几乎等同模型训练误差，这说明系统无论是采样6条模糊规则还是10条模糊规则所构建，模糊神经网络都具有很强的泛化能力，图5也说明这一点。表3列出了D-FNN与RBF-AFS、OLS和ANFIS的比较结果[14-15]。

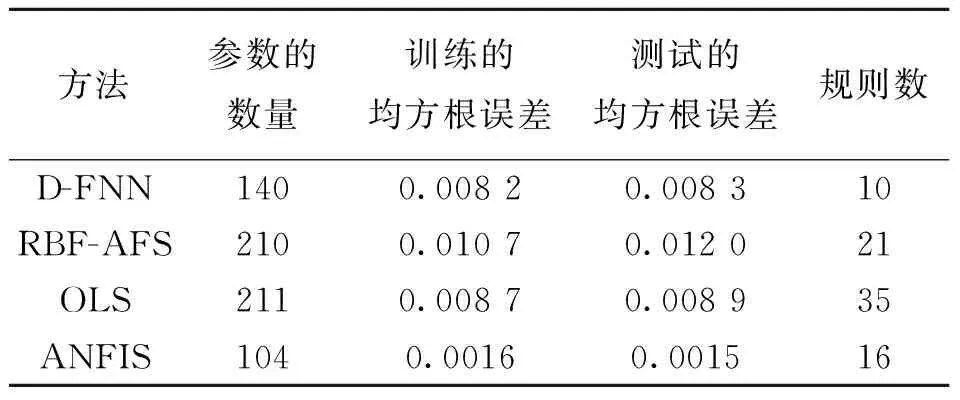
方法参数的数量训练的均方根误差测试的均方根误差规则数D-FNN1400.00820.008310RBF-AFS2100.01070.012021OLS2110.00870.008935ANFIS1040.00160.001516

从比较结果来看，D-FNN有140个可调参数，ANFIS 104个可调参数，但D-FNN的性能也没有ANFIS性能好。原因是ANFIS一个学习过程是基于整个学习样本，通过迭代学习方式进行的，可以达到整体的最优解。D-FNN采用修剪技术在线学习方式，每个样本只学习一次，只能获得次优的结果。然而，D-FNN与也只能得到次优解的OLS、RBF-AFS相比，D-FNN结构更小(修剪技术的使用，结构不会持续增长)而泛化能力更强。

3 结 论

本文把D-FNN算法与其他学习算法进行了比较，并深入探讨了这些算法之间的相互关系。由于修剪技术的使用使得D-FNN具有紧凑的结构和优秀的性能。ANFIS及RBF-AFS一个学习过程是基于整个学习样本，而D-FNN采用占线学习方法，每个数据样本只学习一次，D-FNN学习的快速性是以不能获得最优解为代价的。实验结果表明，对测试数据的误差与对训练数据的训练误差很接近，这说明D-FNN具有很强的泛化能力。直到今天，神经网络结构和泛化能力的研究仍然是神经网络的一个研究热点，引起研究人员的极大兴趣，有关这方面的工作还有待进一步的探究。动态模糊神经网络已经在消费电子、工业控制、系统辨识、模式识别、图像处理等许多领域得到了广泛的应用。

[1] BORS G, GABBOUJ M. Minimal topology for a radial basis functions neural networks for pattern classification[J]. Digital Processing, 2012， 34:173-188.

[2] 任爱红. 模糊随机过程函数列均方差一致Henstock积分的可积性[J]. 中山大学学报:自然科学版, 2010, 51(4): 41-44.

[3] WU S Q, ER M J. Dynamic fuzzy neural networks: A novel approach to function approximation[J]. IEEE Trans Syst, Man, Cybern Part B， 2012， 30: 358-364.

[4] ESPOSITO A, MARINARO M, ORICCHOI D， et al. Approximation of continuous and discontinuous mappings by a growing neural RBF-based algorithm[J]. Neural Networks, 2013，25:651-665.

[5] MYOOD J, DARKEN C J. Fast Leaning in network of locally-tuned processing units[J]. Neural Computation, 2013，1: 281-294.

[6] 杨文光. 权值直接确定的三角型模糊前向神经网络[J]. 中山大学学报：自然科学版，2013,52(2)：33-37.

[7] BORS A G, PITAS I. Median radial basis function neural network[J]. IEEE Trans Neural Networks, 2012，23: 1351-1364.

[8] HAYKIN S. Neural networks, a comprehensive foundation[M]. New York: Macmillan, 2012:465-477.

[9] GIROSI F, POGGIO T. Networks and the best approximation property[J]. Biological Cybernetics, 2012， 63: 169-176.

[10] ER M J. WU S Q. A fast learning algorithm for parsimonious fuzzy neural systems[J]. Fuzzy Sets and Systems, 2009, 126: 337-351.

[11] CHEN S, COWAN C F N, GRANT P M. Orthogonal least squares algorithm for radial basis function network[J]. IEEE Trans Neural Networks, 2011，2:302-310.

[12] LU Y, SUNDARARAJAN N, SARATCHANDRAN P. A sequential learning scheme for function approximation by Using minimal radial basis function networks[J]. Neural Computation, 2012, 19(2):461-478.

[13] KADIRKAMANATHAN V, NIRANJAN M. A function estimation approach to sequential learning with neural networks[J]. Neural Computation,2011， 16(4): 954-975..

[14] CHO K B, WANG B H. Radial basic function based adaptive fuzzy systems and their applications to system identification and prediction[J]. Fuzzy Sets and Systems, 2006,26: 344-354..

[15] JANG J S R. ANFIS: adaptive-network-based fuzzy lnference system[J]. IEEE Trans Syst, Man, Cybern, 2012, 23: 665-684.

The Rule Criteria and Pruning Strategy Based on D-FNN Algorithm Research

ZUOJun,ZHOULing,LIXiaodong

(School of Electronic and Information Engineering,Foshan University,Foshan 528000,China)

A new structure for D-FNN and its learning algorithm are put forward. The structure of this D-FNN is based on RBF neural network. In the new algorithm and structure, generation of fuzzy rule is determined by the output error and the effective radius of the accommodate boundary. At the same time, the application of pruning technology makes a simple network structure, fast learning speed and generalization ability for system. The new algorithm is discussed in detail and compared with correlated algorithms. By these technology methods, the unique advantage of D-FNN is found. At last, simulation program for D-FNN are wrote and the concrete cases are run in the program. Simulation results show that the new D-FNN has a compact structure and excellent performance.

dynamic fuzzy neural network (D-FNN); radial basis function (RBF); fuzzy rule; pruning strategy

10.13471/j.cnki.acta.snus.2015.05.010

2014-12-18

广东省自然科学基金资助项目(S2011020002719)

左军(1958年生)，男；研究方向：智能计算、信息安全、数据库应用;E-mail:13392209106@126.com

TP301.6

A

0529-6579(2015)05-0043-06