凸g-期望的若干性质*

纪荣林，江 龙，石学军

(中国矿业大学理学院，江苏 徐州 221116)



凸g-期望的若干性质*

纪荣林，江 龙，石学军

(中国矿业大学理学院，江苏 徐州 221116)

在倒向随机微分方程生成元满足基本假设的前提下，证明了一个关于凸g-期望和凹g-期望的Sandwich定理。进一步地，得到了一类凸g-期望全体的极小元的存在性，并给出了其极小元性质的等价刻画。

倒向随机微分方程; 凸g-期望; Sandwich定理; 极小元

考虑如下形式的一维倒向随机微分方程(简记为BSDE)：

g-期望的概念可以看成是著名的Girsanov变

换的非线性推广。自从g-期望的概念提出以来，研究者已经得到了关于g-期望的很多性质及其应用。如Chen-Epstein[3]利用g-期望研究了递归效用；Rosazza Gianin[4]首次研究了g-期望与风险度量之间的关系；Jiang[5]则建立了凸g-期望(g-期望诱导的凸风险度量)与生成元g之间的一一对应关系。在Coquet-Hu-Mémin-Peng[6]关于非线性期望的公理化假设框架下，Jia[7]研究了次线性期望的极小元的性质并获得了相应的Sandwich定理。

众所周知，g-期望是一类典型的信息流相容的非线性期望，且是由BSDE诱导出来的而非公理化假设产生的。因此，一个自然的问题是：在g-期望的框架下，关于凸g-期望的极小元的性质刻画及相应的Sandwich定理是否类似成立？

1 预备知识

(A1) (Lipschitz条件) 存在常数K≥0使得dP×dt-a.s.，对任意的(y1,z1),(y2,z2)∈R×Rd，有

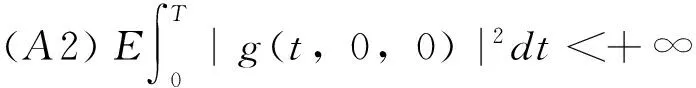
(A3) dP×dt-a.s.，对任意的y∈R有g(t,y,0)≡0。

为方便读者起见，我们回顾Peng[2]关于g-期望和条件g-期望的定义并引入Jia[7]中非线性期望的定义，如下：

(i) 保常数性：ε[c]=c，∀c∈R。

(ii) 单调性：ε[X]≥ε[Y]，若X≥Y，P-a.s.。 (iii) 严格单调性：ε[X]>ε[Y]，若X≥Y，P-a.s.，且P(X>Y)>0。

定义3 称非线性期望ε为凸期望(凹期望)，若其满足

凸性 (凹性)：ε[αX+(1-α)Y]≤(≥)αε[X]+(1-α)ε[Y]，∀α∈[0,1]。

定义4 称非线性期望ε为次线性期望(超线性期望)，若ε是凸期望(凹期望)且满足

正齐次性：ε[λX]=λε[X]，∀λ≥0。

定义5 称非线性期望ε为线性期望，若ε既是次线性期望又是超线性期望。

定义 6 设(S,≤)为一偏序集，称F0为S的一个极小元，若其满足

(i)F0∈S；

(ii) 对任意的F∈S，如果F≤F0，则F=F0。 下面引入本文的一些重要引理，其中引理1来自文[7]推论3.2；引理2和引理3则分别源自文[5]定理3.2及引理2.1。

引理1 设ε1为次线性期望，ε2为超线性期望。若ε1≥ε2，则存在线性期望ε使得ε1≥ε≥ε2。

引理2 设生成元g满足条件(A1)和(A3)，则以下陈述等价：

(i)εg[·]是凸期望；

(ii)g独立于y且关于z是凸的。

引理3 设生成元g满足条件(A1)和(A3)，且g独立于y，则对任意的p∈[1,2)，z∈Rd，有

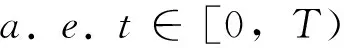
2 主要结果

证明 首先，证明对任意的凸期望ε，定义

(2)

由ε*的定义，立即可得

(3)

(4)

(5)

接下来，有

(6)

事实上，β=0时，由ε*的实值性及(3)式，可得ε*[βX]=0=βε*[X]。令β>0，有

(7)

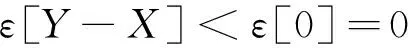
故ε*是次线性期望。

其次，证明对任意的凸期望ε1及凹期望ε2，若ε1≥ε2，则存在线性期望ε使得ε1≥ε≥ε2。事实上，定义

应用引理1，即知存在线性期望ε使得ε1≥ε≥ε2。

最后，证明存在满足题设条件的概率测度Q0，使得εg1≥EQ0≥εg2。由Peng[2]知g-期望是一类典型的非线性期望，结合上一步的结论，我们知道存在一个线性期望ε0，使得

应用引理2知，g1是独立于y的，结合Lipschitz条件，g1(t,0)≡0及比较定理，得

由文[6]定理7.1知, 存在定义在Ω×[0,T]×Rd上的唯一的生成元，记为gQ0，且生成元gQ0满足以下三个假设条件：

(B1) (Lipschitz条件) dP×dt-a.s.，对任意的z1,z2∈Rd，有|gQ0(t,z1)-gQ0(t,z2)|≤K|z1-z2|。

(B2) dP×dt-a.s.，gQ0(t,0)≡0。

由(B3)及条件期望的唯一性，可得

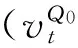
Q0(A)=EQ0[1A]=EQv[1A]=Qv(A)

从而，Q0=Qv。证毕。

定理2 设εg1为凸g-期望，εg2为凹g-期望且εg1≥εg2。令

S={εg:εg是凸g-期望且εg1≥εg≥εg2}

则S至少存在一个极小元，且以下陈述等价：

(i)εg0是S的一个极小元。

(ii)εg0是线性g-期望且εg1≥εg0≥εg2。

εg4[X]≤εg[X]=-εg[-X]≤-εg4[-X]，

0=2εg4[X-X]≤εg4[X]+εg4[-X]

下证(i)⟹(ii)成立。设εg0为S的一个极小元，显然εg0是凸g-期望且εg1≥εg0≥εg2。应用定理1可知，存在一个线性g-期望εg，使得εg1≥εg0≥εg≥εg2，故εg∈S。又εg0为S的极小元且εg0≥εg，则由极小元的定义得εg0=εg。证毕。

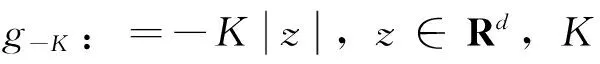
推论1 设εg1为凸g-期望，令

S={εg:εg是凸g-期望且εg1≥εg}

则S至少存在一个极小元，且εg0是S的一个极小元当且仅当εg0是线性g-期望且εg0≤εg1。

推论2 设εg2为凹g-期望，令

S={εg:εg是凸g-期望且εg≥εg2}

则S至少存在一个极小元，且εg0是S的一个极小元当且仅当εg0是线性g-期望且εg0≥εg2。

推论3 设S为所有凸g-期望的全体，则S至少存在一个极小元，且εg0是S的一个极小元当且仅当εg0是线性g-期望。

[1] PARDOUX E, PENG S G. Adapted solution of a backward stochastic differential equation [J]. Systems Control Letters, 1990, 14: 55-61.

[2] PENG S G. BSDE and related g-expectation [J]∥ Backward stochastic differential equations. KAROUI N E，MAZLIAK L, eds. Pitman Res Notes Math Ser, 1997, 364: 141-159.

[3] CHEN Z J, EPSTEIN L. Ambiguity,risk and asset returns in continuous time [J]. Econometrica, 2002, 70: 1403-1444.

[4] ROSAZZA GIANIN E. Risk measures via g-expectations [J]. Insurance: Mathematics and Economics, 2006, 39: 19-34.

[5] JIANG L. Convexity,translation invariance and subadditivity for g-expectations and related risk measures [J]. Annals of Applied Probability, 2008, 18: 245-258.

[6] COQUET F, HU Y, MÉMIN J, et al. Filtration consistent nonlinear expectations and related g-expectation [J]. Probability Theory and Related Fields, 2002, 123 (1): 1-27.

[7] JIA G Y. The minimal sublinear expectations and their related properties [J]. Science in China Series A: Mathematics, 2009, 39: 79-87．

[8] CHEN Z J, KULPERGER R. Minimax pricing and choquet pricing [J]. Insurance: Mathematics and Economics, 2006, 38(3): 518-528.

[9] CHEN Z J, CHEN T, DAVISON M. Choquet expectation and Peng’s g-expectation [J]. The Annals of Probability, 2005, 33(3): 1179-1199.

[10] HE K, HU M S, CHEN Z J. The relationship between risk measures and choquet expectations in the framework of g-expectations [J]. Statistics and Probability Letters, 2009, 79: 508-512.

Some Properties of Convexg-Expectations

JIRonglin,JIANGLong,SHIXuejun

(School of Sciences, China University of Mining and Technology, Xuzhou 221116, China)

Under the basic assumptions on generators，a sandwich theorem for convexg-expectations and concaveg-expectations is proven. Furthermore，for some subsets of all convexg-expectations, the existence of their minimal members are proven and the properties of those minimal members are characterized.

backward stochastic differential equation; convexg-expectation; sandwich theorem; minimal member

10.13471/j.cnki.acta.snus.2015.05.003

2015-01-09

国家自然科学基金资助项目(11371362)；2014年江苏省普通高校研究生科研创新计划资助项目(KYZZ_0373)

纪荣林 (1984年生)，男；研究方向：非线性数学期望；通讯作者：江龙;E-mail:jianglong365@hotmail.com

O211.67

A

0529-6579(2015)05-0011-04