改进GEP在仪器稳定度预测中的应用

程双江 李世平 邬肖敏

(第二炮兵工程大学，西安 710025)



改进GEP在仪器稳定度预测中的应用

程双江 李世平 邬肖敏

(第二炮兵工程大学，西安 710025)

提出了一种基于基因表达式编程(GEP)的仪器稳定度预测新方法，为了提高预测精度，将相空间重构应用到仪器稳定度的序列分析中，采用了变种群策略与保留精英个体的轮盘赌选择策略；同时针对标准GEP在解码过程中种群、测试数据集和进化代数等参数较大时适应度值计算耗费时间和空间较大的问题，结合GPED和GRCM算法，对其进行改进。将改进后的GEP用于高稳时频晶振计量标准仪器的稳定度预测中，结果表明预测效果较好。

相空间重构;GEP;变种群策略;稳定度预测

0 引言

仪器是人类认识世界的重要工具，广泛应用于社会生活的各个领域，然而随着电子技术的发展，尤其是对于目前的智能仪器而言，仪器精度往往能达到很高的要求，因此在测量精度相当的前提下，稳定度指标正在逐步取代精度成为用户最关心的问题，尤其对于部分产业而言，稳定度不好造成的影响往往比仪器精度下降产生的影响要大得多，而且对于维修人员来说，稳定度不好的仪器，其维护量也比精度差的仪器要大得多，因此对于稳定度进行预测具有现实意义。考虑到我们日常所使用的仪器设备不可能在每一次的使用前都对其进行检测，一般仪器的检定周期为一年、两年不等，要想更好地把握其性能指标在未来可能的变化趋势，预测就显得尤为重要。科学的预测是正确决策的依据和保证[1]。多年以来，国内外许多专家和学者对预测理论不断探索，形成了一系列行之有效的预测方法,常用的方法包括灰色预测、随机时间序列预测、神经网络预测和支持向量机预测[2]等。而基因表达式编程(GEP)作为一种新型的时间序列预测方法[3]，无需人为的选择数学模型，就可以实现复杂系统的非线性建模，尤其对于小样本、非线性序列预测效果较好。

文献[4]将GEP运用到股票指数和价格时间序列预测分析，文献[5]将GEP用于人口预测，文献[6]将GEP应用到短期电力系统负荷预测当中，都取得了很好的效果，并通过实例分析了GEP相比于遗传算法、神经网络、灰色系统模型的巨大优势，然而将预测理论应用到仪器稳定度预测方面的研究并不多，尤其是GEP预测，基本还无人涉及。因此本文将GEP理论引入到仪器稳定度预测当中，为了提高预测精度与收敛速度，引入相空间重构理论，同时对标准GEP的解码算法及遗传过程进行改进。将改进后的GEP用于高稳时频晶振计量标准仪器稳定度预测当中，并与简单移动平均模型、ARMA模型预测结果进行比较，验证该方法的有效性。

1 GEP概述

基因表达式编程(GEP)是葡萄牙科学家Candida Ferreira在2001年提出的一种基于基因型和表现型的基因算法，具有更强的解决复杂问题的能力、极强的函数发现能力和很高的编程效率,相比遗传算法(GA)和遗传编程(GP)高出2～4个数量级。GEP同时兼备了GA和GP的优点，与GA和GP相比，GEP最大的优势在于在句法上将个体先编码为固定长度的线性串，在语义上再表示成大小、形状都不同的非线性实体[7]，这样就具备了利用简单编码解决复杂问题的能力，克服了GA和GP各自的不足。

每个GEP的染色体可以由多个基因通过一定的连接运算符连接，而每个基因又可分为头部(h)和尾部(t)，头部包含了终结符和函数集中的函数,而尾部只能包含终结符，头部的大小根据具体的问题在初始参数时自己设定，而尾部则依据下面的公式计算给出：

t=h×(n-1)+1

(1)

式中，n为函数符集中函数的最大操作数目。

这样的编码方式可以保证基因在进行遗传操作时始终保持其有效性。一个包含了函数集F={+,-,*,/,Q}和终结符T={x,y,z}，头部为h=5基因编码如下：

+Q/x*yxxzyy

(2)

则其表现型可按照规则解码如图1所示。

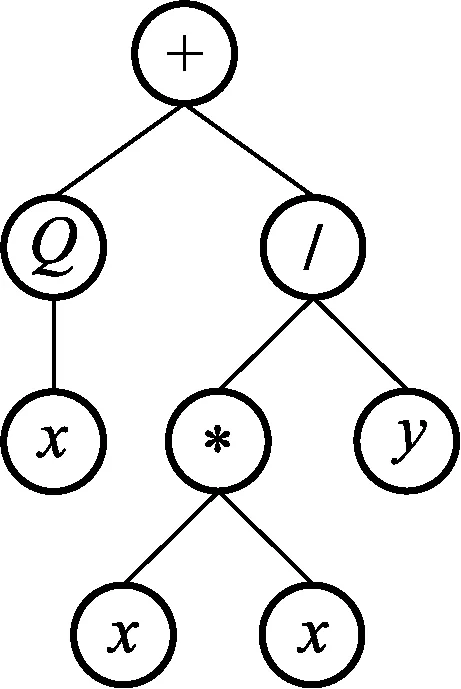
图1 GEP表达式树

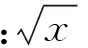
图2 GEP算法流程

通过对基因进行不断的迭代，就可以实现沿着预测值与实际值误差最小的方向进化，达到建模拟合，实现最终预测的目的。由于GEP建立的非线性预测模型是一个具体的表达式，这样就方便我们进行分析，同时对于小样本数据而言，采用GEP预测，可以有效回避神经网络等方法中出现的过拟合问题。

2 相空间重构技术与改进GEP算法

2.1 相空间重构技术

相空间重构技术的基本思想是:系统中任一状态分量的演化都是由与之相关的其它状态分量所决定的,因此这些相关状态分量的信息就隐含在任一状态分量的发展过程中[9]。为了重构一个等价的状态空间，只需考察一个状态分量，将它在某些固定时间延迟上的测量值作为新维处理，从而通过这种类似嵌入的方法构造出一个等价的相空间。研究已经证明，当嵌入维数M和时间延迟t 选择适当时，重构出来的相空间具有与实际动力系统几乎相同的几何性质和信息性质。因此可以将其应用到时间序列分析当中，将一维的时间序列：

x(t)t=1,2,…n

(3)

转换为M维向量：

X(t)={x(t),x(t+t ),…,x[t+(M-1)t ]}

t=1,2,…,n-(M-1)t

(4)

相空间重构的关键在于嵌入维数M和时间延迟t 的确定,两者的确定方法有很多，一种方式认为两者不相关，此时嵌入维数的确定主要方法有虚假最近邻点法和奇异值分解法等，时间延迟的确定方法有自相关函数法、互信息法和平均位移法等；另一种认为两者是相关的，主要方法包括时间窗口法、C-C法、嵌入维时间延迟自动算法[10]。本文采用C-C法进行嵌入维数M和时间延迟t 两参数的确定。

2.2 解码算法的改进

在GEP算法中，为了评估染色体的优劣，必须首先进行解码，然后再进行适应度值的计算。标准的解码过程是先构造种群中每个染色体对应的表达式树，然后通过多次中序遍历每个表达式树来完成适应度计算。然而若种群测试数据集和进化代数等参数较大，则进行适应度计算时构建和遍历表达式树的操作次数会很大，导致适应度计算的时间和空间耗费较大[11]。因此无需构造表达式树实现直接解码就成了研究的热点。本文结合GPED和GRCM算法，提出了一种新的无需构造表达式树的解码算法，首先利用GPED算法进行有效基因长度的确定，然后利用GRCM算法进行解码操作。

GPED算法进行有效基因长度的确定原理可以表述如下：首先设置一个计数变量nCount并初始化为1，从左到右逐个读取基因中的字符；其次观测基因中的字符，如果为函数符，则nCount加上n-1，其中n为该函数的操作数目；如果为终结符，则nCount减去1,直至nCount为0为止停止读取基因；最后记录所读取的基因字符个数即为有效基因长度。然后利用GRCM方法进行解码，过程如下:

1)寻找最后一位函数符，如果是单目运算符，则从有效基因的尾部选择一位进行运算，如果是双目运算符，则从有效基因的尾部选择两位进行运算，以此类推。

2)将运算的结果作为终结符保存在该函数符的基因位，同时基因的有效长度减去相应的运算位数，此时基因就进行了适当的更新。

3)从更新后的新基因中选择最后一位运算符，进行步骤1)和步骤2)操作，直至基因有效长度个数为1。

4)记录此时长度为1的基因终结符数值，即为该基因的解码值。

以基因+Q-/b*aaQbaabaabbaaab为例进行分析，利用GPED算法可以得到该基因的有效长度为11，然后从最后一位运算符(Q)开始运算，其解码过程如图3所示。

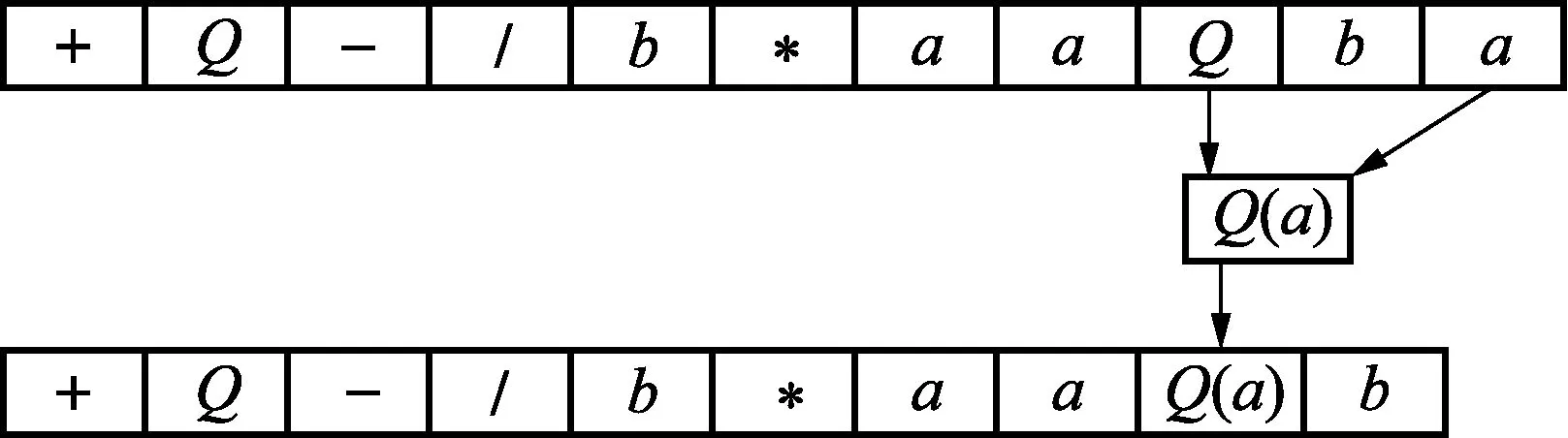
图3 解码过程

2.3 种群个体的选择与变种群策略

在种群的进化过程当中，初始化基因往往起着至关重要的作用，因此在种群初始化的过程中，采取基于精英个体的产生策略，即使第一个个体具有较高的适应度，其他种群则随机产生，这样可以提高进化效率；同时在进化选择的过程中，采取了保留精英个体的轮盘赌选择策略，复制上一代种群中的最优个体直接到下一代的第一个种群；最后为了提高种群的多样性，避免陷入局部最优解，采取了变种群策略，即在初期给定一个初始种群数，随着时间的推移，种群的多样性会随之下降，因此达到一定代数之后，每隔一定代数，适当增加种群的个数，增加的种群个体采用随机方式产生，这样可以显著提高种群多样性，考虑到种群代数的增加是以牺牲程序运行时间为前提的，因此种群代数不能无限制的增加，事先设定一进化代数，达到该进化代数后种群个数不再发生变化，但是在选择的过程中附加了少量种群的随机化，即部分个体不是通过选择产生而是随机产生。

3 实例分析

计量标准仪器是保障其他仪器测量量值准确、统一的物质基础，对其进行预测是进行计量标准全寿命周期质量控制、管理与检测的主要手段。对于高稳时频晶振计量标准仪器来说，稳定度指标尤为重要。本文采用某计量站高稳时频晶振计量标准仪器进行实例分析。

数据来源于该仪器每年一次的上级单位检定数据(作为第一季度数据)，以及两次检定期间，该计量站计量员利用更高精度的计量标准每季度进行一次的检定数据(第一季度除外)。从2002年到2012年总共44个数据点，如表1所示。

本文以2002—2011年的40个数据点进行稳定度拟合，预测2012年4个季度的稳定度值。

首先通过C-C法寻找最优的嵌入维数M和时间延迟t 分别为6和1，这样输入时间序列就转换为

(5)

i=1,2,…,6

模型就转化成了6输入单输出的GEP模型，GEP参数设置如表2所示。

表1 高稳时频晶振2002—2012年稳定度值(×10-12)

表2 GEP参数设置

续表

在确定相空间重构相关参数后，对数据进行必要调整，而后就可以利用改进后的GEP模型进行2002-2011年的数据拟合以及2012年的稳定度预测，经整理后得到的预测模型公式为

X6+sin{cos[exp(cos(X6-X5))]}+

cos[cos(3.58+X1)-0.099]

(6)

得到的拟合曲线如图4所示，可以看出，拟合曲线与原始曲线吻合度较高，拟合效果较好，因此可以用此模型进行预测。

为了检验改进后的GEP模型在稳定度预测方面的巨大优势，分别用简单移动平均预测模型、ARMA模型以及标准的GEP对其进行预测，与实际值进行比较。4种模型得到的2012年4个季度的预测值如图5所示。

为了更加直观的检测预测效果，以平均相对误差作为衡量标准，4种模型的预测值和相对误差如表3所示。

从表3可以看到简单移动平均预测模型，ARMA模型，标准的GEP模型和改进后的GEP模型平均相对误差分别为26.5%,6.6%,6.1%,2.2%，因此可以认为GEP模型在小样本仪器稳定度预测方面具备更高的精度，可以作为仪器稳定度预测方面的一种新方法，同时也看到改进后的GEP预测模型性能得到了进一步的提升。

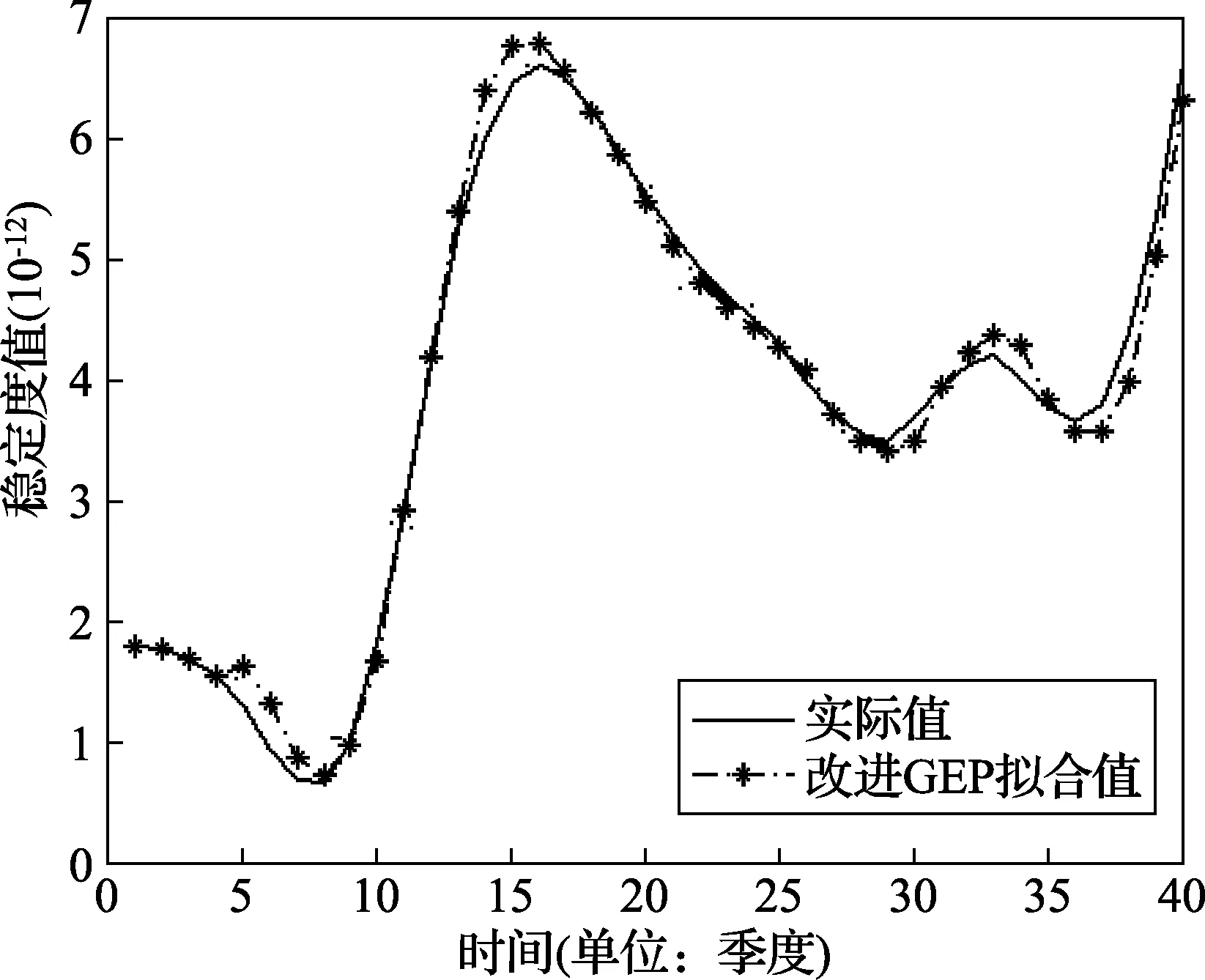
图4 改进GEP拟合曲线图

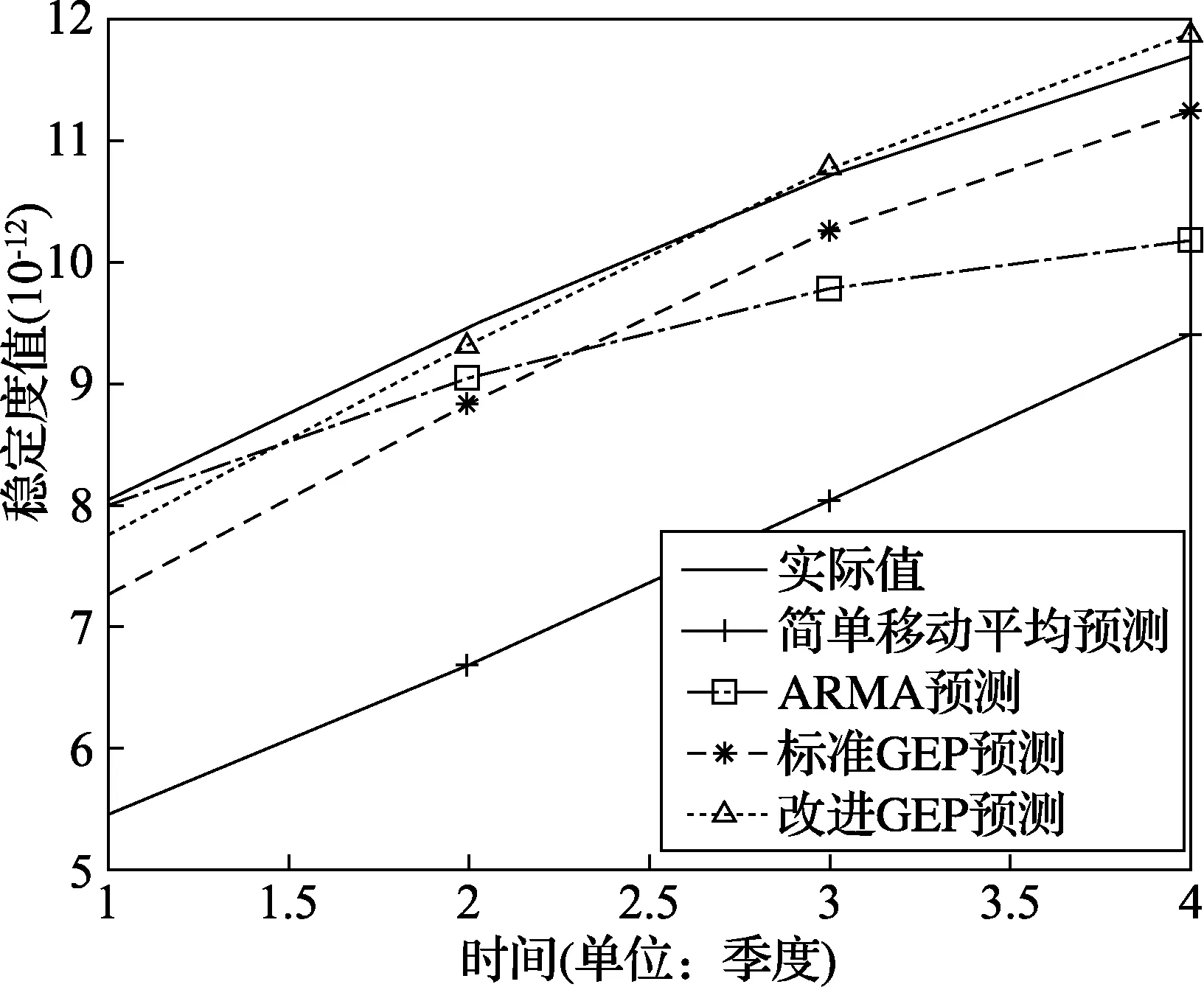
图5 2012年不同模型稳定度预测值

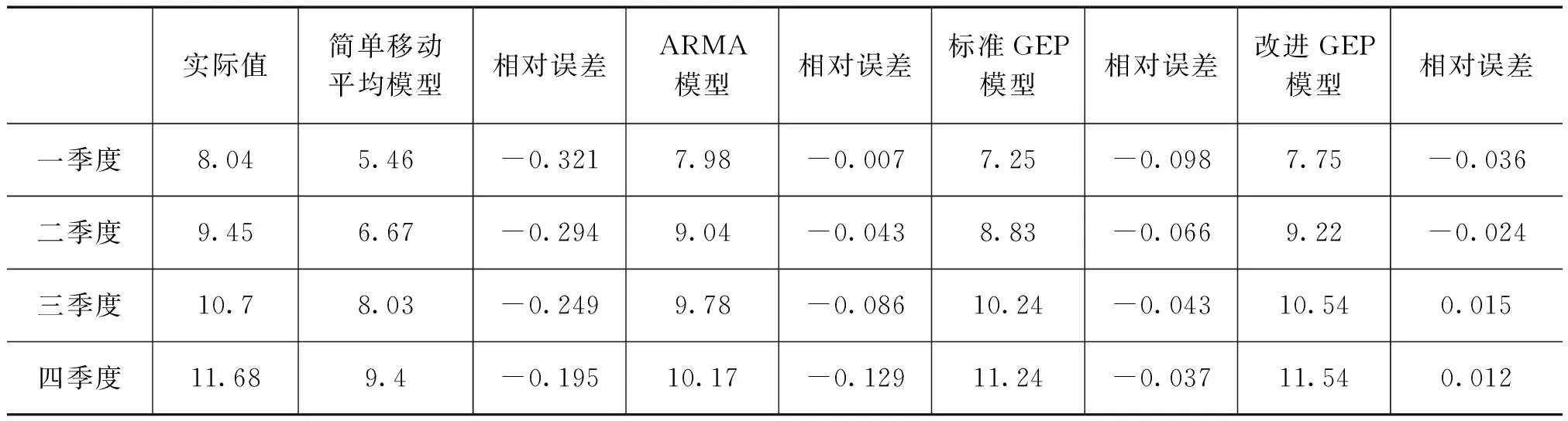
表3 4种模型2012年稳定度预测结果 (×10-12)

4 结束语

采用GEP模型实现了仪器稳定度的预测。首先通过相空间重构法将单输入的时间序列转换成了多输入的序列；其次针对标准GEP算法在解码过程中过于复杂导致计算效率不高的问题，对解码过程进行了改进；最后对遗传过程进行了优化，采取了变种群策略。通过与简单移动平均预测模型、ARMA模型和标准GEP模型之间的比较，可以得出结论：GEP在仪器稳定度预测方面具有很高的精度与很大的研究价值，改进后的GEP预测精度与运算效率均得到了进一步的提升。

[1] 康重庆,夏清,刘梅.电力系统负荷预测[M].北京,中国电力出版社,2008

[2] 吴德会.基于最小二乘支持向量机的传感器非线性动态系统辨识[J].计量学报，2008，29(3)

[3] 彭昱忠,等.基因表达式编程的理论研究综述[J].计算机应用研究，2011,28(2):413-418

[4] 廖勇.基于基因表达式编程的股票指数和价格时间序列分析[D].成都：四川大学,2005

[5] 刘萌伟,黎夏,刘涛.基于基因表达式编程的人口预测模型[J].中山大学学报,2010,49(6):115-120

[6] 霍利民,等．基于基因表达式程序设计及误差循环补偿的电力系统短期负荷预测[J]．中国电机工程学报,2008，28(28)：103-107

[7] Ferreira C.Gene expression programming: A new adaptive algorithm for solving problems[J].Complex Systems, 2001,12(2):87-129

[8] 彭显忠.基因表达式编程改进算法及其在函数优化中的应用[D].广西：广西师范学院,2009

[9] 张强等.基于相空间重构技术的金融系统混沌识别[J].经济数学，2011,28(2):40-43

[10] 霍峥嵘.相空间重构法在齿轮故障诊断中的应用[J].机械与电子，2010(35):126-127

[11] 元昌安，等.基因表达式编程算法原理与应用[M].北京：科学技术出版社,2010

10.3969/j.issn.1000-0771.2015.09.09