基于定频变点采样技术的电网谐波检测方法
2015-06-07王柏林
梅 永 王柏林
(1.南京信息工程大学 电子与信息工程学院,南京 210044;2.河海大学 能源与电气学院,南京 210098)
基于定频变点采样技术的电网谐波检测方法
梅 永1王柏林2
(1.南京信息工程大学 电子与信息工程学院,南京 210044;2.河海大学 能源与电气学院,南京 210098)
本文提出了一种新的定频变点电网谐波检测方法。首先对电网信号进行定频整周采样,即以恒定采样频率fS对电网电压(电流)波形采样,由过零检测器控制每个数据窗口无限逼近整数(S)个周波,然后对采样信号进行变点DFT计算。事先把不同点数的DFT系数预存在大容量flash存储器中。本文采用定频变点法实现同步采样,同步偏差一定小于1/L0(L0=SfS/55),只要选取足够大的采样频率fS和采样周期数S,采样同步偏差就足够小,不存在时延,从而减少了谐波测量同步误差。
定频整周采样;过零检测;变点DFT; 谐波测量
0 引言
谐波研究的意义,首先是因为谐波的危害十分严重。谐波使电能的生产、传输和利用的效率降低,使电气设备过热、产生振动和噪声,并使其绝缘老化,使用寿命缩短,甚至发生故障或烧毁[1]。其次,谐波研究的意义还可以上升到从治理环境污染、维护绿色环境的角度来认识。对电力系统这个环境来说,无谐波就是“绿色”的主要标志之一。因此电力系统谐波电压测量[2-4]、谐波电流测量[5-6]、随机环境下的谐波分析[7-9]、谐波状态估计[10]、电能质量特征参量的提取[11]具有重要的意义。为此许多学者对电能质量问题尤其是谐波测量进行广泛研究,也作出了重要的贡献[1-16]。提出了许多谐波测量算法,从早期的模拟滤波器法到傅里叶变换[2-3]、小波变换[14]、希尔伯特黄变换[12-13]、其他算法[14-16]等。
虽然各种新的谐波测量算法层出不穷,由于各种原因大部分算法在工程中的应用还不够成熟和完善。在电力工程中真正广为应用的仍然是FFT算法,IEC61000-4-7谐波测量标准推荐的测量算法也仍然是FFT算法。这一事实说明:1)基于FFT的谐波测量算法仍然具有很强的应用价值和研究意义;2)许多新的谐波测量算法还要在工程应用上狠下功夫;3)FFT算法与新算法的融合可能是拉近研究与应用的一条途径。
1 非同步采样下的采样误差分析
电力系统谐波测量的常用方法是FFT(快速傅立叶变换)法,其基本原理是:首先对电网波形采样和ADC(模数转换)得到采样序列,然后对采样序列进行FFT得到各次谐波、间谐波的幅值和相位信息。FFT是DFT(离散傅立叶变换)的快速算法,在数据点数很多时,FFT比标准DFT快得多,但FFT要求数据点数必须是2的整次幂。理论上,FFT方法要求同步采样,即等间隔整周期采样—— 同一数据窗口数据的采样周期相等且每个数据窗口的时宽刚好等于整数个电网周波。由于电网频率是不断变化的,同步采样很难实现,所以,数据总存在采样同步偏差,采样同步偏差直接造成各次谐波、间谐波的幅值和相位的测量误差,这称之为谐波测量同步误差。
经过理论分析和仿真验证,同步误差越大造成谐波幅值误差越大;同步偏差一定的情况下,幅值较小的谐波产生的测量相对误差越大[17]。
目前减少采样采样同步偏差的方法主要有:1)硬件同步:主要指加PLL(锁相环)的同步方法;2)软件同步:利用DSP的定时器实时改变采样频率。硬件同步和软件同步的采样频率都是变化的,但每一数据窗口内的采样点数相同且都是2的整次幂。PLL同步是IEC61000-4-30标准推荐的方法,IEC61000-4-30标准要求PLL的采样同步偏差不大于万分之三。电网频率恒定不变时PLL做到万分之三就不容易了,更何况电网频率时刻都在波动,PLL时刻都处在闭环调节的动态过程之中,这种闭环调节还存在时延,所以实际应用中PLL很难保证采样同步偏差不大于万分之三,传统的硬件同步和软件同步在实际应用中都不容易获得高精度。IEC61000-4-30(2003)标准还要求FFT加矩形窗,Matlab仿真表明:同步偏差为万分之三时,矩形窗FFT对40次以上的谐波、间谐波的计算结果就是超标的。软件同步可以看作是一个软件PLL,除了上述弊端,软件同步比硬件PLL的时延大,因为后者是锁相、前者是锁周。锁周是用前一个周波的宽度确定下一个周波的采样周期,时延至少是一个周波。软件同步还有个问题就是定时器的分数定时误差。
本文提出一种固定采样频率、采样点数可变的采样技术,能很好的减少同步偏差造成的谐波测量误差。
2 定频变点采样方法
所谓定频变点采样技术是以恒定采样频率fS对电网电压(电流)波形采样,由过零检测器控制每个数据窗口无限逼近S个整周波;用固定的采样频率fS对电网波形采样,允许采样频率很高,而且越高越有利。
例如一个数据窗口的时间宽度规定为S个电网整周波,S个电网周波的开始(电网波形过零)采当前数据窗口的第1点,S个电网周波的结束(电网波形过零)停止本数据窗口的采样,采样同时计算采样点数Lk。按IEC61000-4-30标准的要求采样周波数S=10。
设Lk的可能取值是:
L0,L0+1,…,L0+n,…,L0+N-1,其中L0、n、N为正整数,N个Lk分别对应第1,2,…,n,…,N组DFT系数,根据三角函数的循环性,第n组DFT系数只需存储L0+n个三角函数值,不需要存2M(L0+n)个三角函数值。
考虑电网频率f波动的最大范围为45~55Hz, 如果采样频率fS和数据窗口的周波数S都固定不变,那么f=55Hz时的采样点数L0最小:
f=45Hz时的采样点数L0+N-1最大:
其中,round{ }表示取整运算。
3 变点数DFT计算谐波参数
设当前数据窗口的采样点数为Lk,且Lk个采样数据(采样序列)为:
y=[y(1)y(2) …y(Lk)]
当前数据窗口的采样结束后立即计算Lk点实序列三角函数型DFT:
X=FyT
式中,yT表示向量y的转置;F为实序列三角函数型DFT的系数矩阵:
其中,M是要求的频点数。按IEC61000-4-30标准的要求:需要测量谐波、间谐波共500个频点即M=500。一次DFT需完成500×Lk次乘加运算。
以前由于计算机的数据处理能力不高,DFT曾经是难以实施的,如今高速DSP(数据处理器)的出现已经使得直接用DFT作为谐波分析的工具成为现实。DFT的最大优势在于不要求一个数据窗口的采样点数是2的整次幂,我们则进一步发展为:不要求每个数据窗口的采样点数相同即变点DFT。
为了提高DFT的计算速度,我们采取了两个措施:
1)不是进行Lk×Lk次乘加运算,而是进行500×Lk次乘加运算,因为高于50次的谐波、间谐波不需要测量。
2)不同点数的DFT系数(系数矩阵F的元素)用查表法得到。把不同点数的DFT系数预存在大容量flash存储器中,设Lk的可能取值是L0,L0+1,…,L0+n,…,L0+N-1,它们分别对应第1,2,…,n,…,N组DFT系数,根据三角函数的循环性,第n组DFT系数只需存储L0+n个三角函数值,不需要存2M(L0+n)个三角函数值。
采取了这两个措施的DFT比FFT慢不了多少,用现代DSP足以从容地完成。
4 仿真研究
给出仿真模型如下:
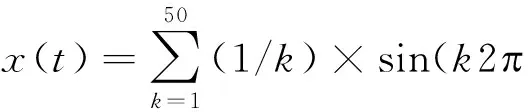
取DSP定时器工作频率为150MHz,取采样率fS=60kHz、采样周期S=10,计算出采样点数L0=10909,采样同步偏差小于万分之一。表1是不同电网频率下,本算法所得到的谐波幅值的相对误差(Matlab仿真结果):
表1中,E1、E2、E3、E25、E31、E48、E49、E50分别代表第1、2、3、25、31、48、49、50次谐波幅值的相对误差。可见,本方法很容易使谐波精度达标。
5 结论
本文不用传统的硬件同步和软件同步,而是采用定频变点法实现同步。即固定采样频率,不需要每个数据窗口的采样点数相同, 解决了各个数据窗口的数据点数不同且不是2的整次幂的问题,这种方案即使在电网频率不断波动的情况下,也能实现同步偏差小于万分之一、甚至更小,不存在时延。减少了采样同步偏差就直接减少了谐波测量误差。对于不同点数的DFT的系数利用可编程片上系统计算出来存在数据存储器里,供DSP实时计算谐波测量值查表,这样大大节省了运算时间,提高了谐波分析的实时性。本文提出的减少采样同步偏差的方法有如下特点:
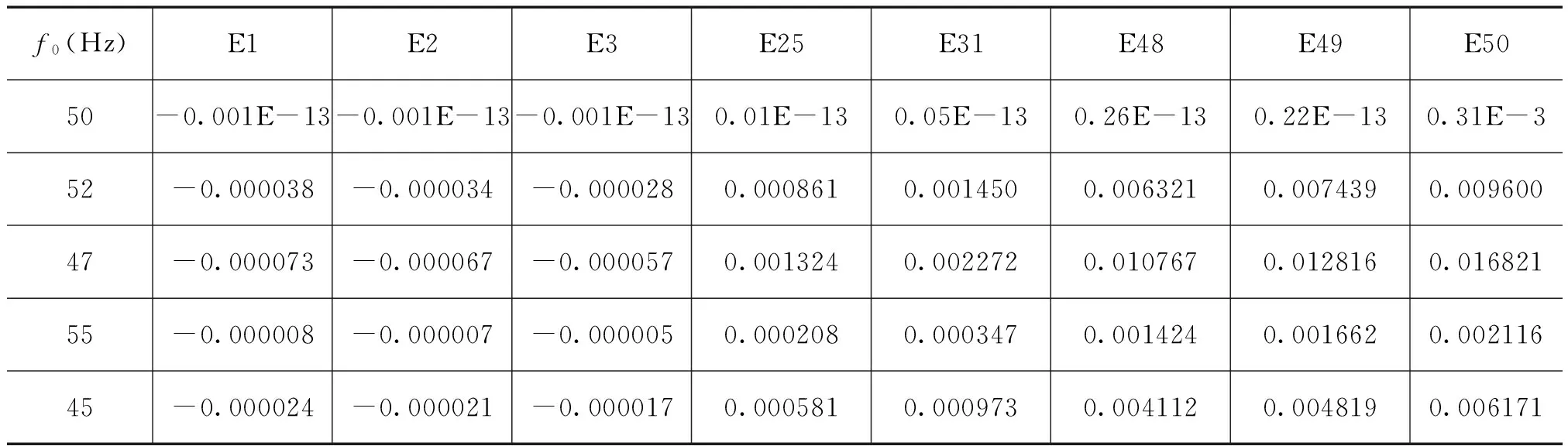
表1 谐波幅值的相对误差matlab仿真结果表
1)结构简单、易实现,定频整周采样器可以用过零检测器加ADC构成,变点DFT计算器可以用高速DSP(或PSOC)加flash存储器构成,不需要常见的PLL同步环节;
2)很容易做到采样同步偏差小于万分之一、甚至更小,而传统的硬件同步和软件同步方法很难做到采样同步偏差小于万分之一;
3)电网频率波动与电网频率相对稳定时的采样同步偏差基本一致,而传统的硬件同步和软件同步在电网频率波动时的采样同步偏差比电网频率相对稳定时大得多;
4)同步不存在时延,而硬件同步和软件同步同步都存在时延;
5)极小的采样同步偏差保证了极小的谐波测量误差。
[1] 林海雪.公用电网谐波国标中的几个问题[J].电网技术,2003,27(1)
[2] 刘敏,王克英. 基于快速傅里叶变换与误差最小原理的谐波分析方法[J].电网技术,2006,30(19)
[3] 薛蕙, 杨仁刚. 基于FFT 的高精度谐波检测算法[J].中国电机工程学报, 2002, 22(12)
[4] 李明,王晓茹.采用时频原子方法的电压闪变检测[J].电网技术,2010,34(7)
[5] 戴朝波,林海雪. 两种谐波电流检测方法的比较研究[J].中国电机工程学报,2002,22(1)
[6] 刘国海,吕汉闻,刘颖,等. 基于改进RLS 算法的谐波电流检测方法[J]. 电力自动化设备,2010,30(10)
[7] L. Sainz, M. Caro, J. Pedra, Study of electric system harmonic response,IEEE Trans. Power Deliv. 19 (2) (2004) 868-874.
[8] L. Sainz, J. Pedra, M. Caro, Steinmetz circuit influence on the electric system harmonic response, IEEE Trans. Power Deliv. 20 (2) (2005)
[9] 刘应梅,高玉洁.基于Prony 法的暂态扰动信号分析[J].电网技术,2006,30(4)
[10] 梁志瑞, 叶慧强, 赵飞. 电力系统谐波状态估计研究综述[J].电力系统保护与控制, 2010, 38(15)
[11] 贾清泉,于连富,董海艳,等.应用原子分解的电能质量扰动信号特征提取方法[J].电力系统自动化,2009,33(24)
[12] 张宇辉,贺健伟,李天云,等.基于数学形态学和HHT 的谐波和间谐波检测方法[J].电网技术,2008,32(17)
[13] 苏玉香,刘志刚,李科亮,等.Hilbert-Huang 变换在电气化铁路谐波检测中的应用[J].电网技术,2008,32(18)
[14] 汪斌,王年,蒋云志,等.改进FastICA 算法在谐波检测中的应用[J].电力自动化设备,2011,31(3)
[15] 郭成,李群湛,贺建闽,等.电网谐波与间谐波检测的分段Prony算法[J].电网技术,2010,34(3)
[16] 赵闻蕾,邹积岩,孔莉,等.基于小波变换的电气化铁道牵引负荷谐波分析[J].铁道学报,2011,33(6)
[17] 梅永,王柏林.电力系统谐波分析的同步校正法.电力自动化设备, 31(1)
10.3969/j.issn.1000-0771.2015.09.03
