太岳山隧道施工优化及数值模拟分析

宋 力

(中铁三局集团有限公司，山西 太原 030001)

太岳山隧道施工优化及数值模拟分析

宋 力

(中铁三局集团有限公司，山西 太原 030001)

针对太岳山隧道施工过程出现的顶部岩层掉块垮塌、台阶法步长不协调以及台阶高度与格栅钢架高度不匹配等工程问题，提出了施工优化方案，并采用数值计算方法对优化前后的施工方案进行了模拟分析，计算表明：优化后的施工方案有效地保证了隧道的施工质量和施工进度。

隧道工程，泥岩，上下台阶法，施工优化，数值分析

随着国民经济的快速增长，我国交通建设领域得到了迅猛发展，穿越山岭地区的隧道工程也越来越多。据不完全统计，我国目前建成的铁路隧道总长度已达到7 000多千米，公路隧道总里程达到3 000多千米，到2020年前，我国规划建设5 000座隧道，长度超过9 000 km。同时，在隧道工程的众多技术领域，众多工程技术人员做出了大量的努力和杰出的贡献，并取得了举世瞩目的成就[1]。

然而，由于岩体工程的极其复杂性，目前工程界还远未能解决隧道工程中所遇到的各类问题，致使隧道工程长期处于“经验设计”和“经验施工”的局面[2]。因不同隧道所处工程地质坏境的差异，仅依靠经验来进行隧道设计和施工难免造成与实际不符。因此，不少学者则依据隧道施工过程中实际开挖揭露的工程地质情况，对隧道的设计和施工方案进行优化。如李术才等[3]以八字岭分岔隧道为例，对分岔隧道的稳定性及其施工优化进行了分析研究；胡世权[4]开展了龙潭隧道页岩段施工优化的数值模拟分析；杨凡杰等[5]基于锦屏大理岩循环加卸载试验提出了弹塑性耦合力学模型，对锦屏二级水电站引水隧洞进行了计算分析；赵玉光等[6]以对广惠高速公路小金口双连拱隧道为例，对双连拱隧道施工过程进行了数值模拟，并对施工方法进行了比选；佘健等[7]对渝黔二期工程笔架山隧道的软弱围岩段施工过程中进行了三维弹塑性数值模拟分析。

本文将在已有研究基础上，针对太岳山隧道在施工过程中所遇到的问题，对其施工方案进行优化，并对优化前后的施工方案进行数值模拟对比分析，最后，结合数值计算结果和现场实际情况对优化后施工方案的合理性进行评价。

1 工程概况

太岳山隧道是山西中南部铁路通道的重、难点工程，也是控制工程。隧道起讫里程为DK392+930～DK409+124，全长16 194 m。太岳山隧道为单洞双线隧道，开挖断面93 m3～110 m3。开挖宽10 m～11 m，高9 m～10 m，隧道设4座施工斜井作为辅助坑道。太岳山隧道洞身最大埋深约300 m，最小埋深约5 m，隧道开挖区域地应力以自重应力为主。

隧道位于中低山丘陵区，通过地层主要二叠系下统上石盒子组砂岩夹泥岩、上石盒子组砂岩夹泥岩，石千峰组泥岩夹砂岩。其中，泥岩岩质较软，易崩解，具膨胀性，而砂岩岩质较硬，风化层厚8 m～12 m；全隧道估算正常涌水量8 594 m3/d，最大涌水量20 393 m3/d。主要不良地质为进口段浅埋黄土以及全隧道水平泥岩夹砂岩易垮塌地层。

2 优化前隧道施工方案及工程问题

由于太岳山隧道为单洞双线隧道，优化前的施工方案主要采用传统的双线隧道台阶法施工。根据传统双线隧道台阶法施工的要求，施工时上台阶要满足挖掘机和凿岩台架的布置要求，一般上台阶高度控制在6 m左右，上台阶的台阶长度10 m～20 m，下台阶至仰拱施工距离在20 m左右(见图1)。

在太岳山隧道的施工初期，按传统的双线隧道台阶法施工，施工过程出现如下几种不利的工程情况：

1)爆破后初期支护期间顶部水平岩层经常出现掉块垮塌现象；2)由于出碴时凿岩台架和出碴设备的空间问题，台阶法步长关系不能保证，或因为保证安全的步长关系不能保证上下台阶同步推进，严重影响施工进度；3)水平岩层拱部须架设格栅钢架时，台阶高度与格栅钢架高度不匹配，格栅钢架立设难度大。

3 优化后隧道施工方案

针对上述太岳山隧道施工初期的不利工程情况，为保证在水平泥岩夹砂岩且易垮塌地层实现快速安全施工，对隧道初始施工方案进行了优化。具体如下：将台阶法施工时的上台阶高度调整为3.6 m左右，上台阶钻爆作业采用简易平台(马凳)，上台阶长度控制到3 m～5 m；下台阶高度则调整为6 m左右，下台阶施工采用凿岩台架施工，下台阶至仰拱的施工距离为20 m左右，这样掌子面至仰拱的距离始终控制在35 m之内(见图2)。

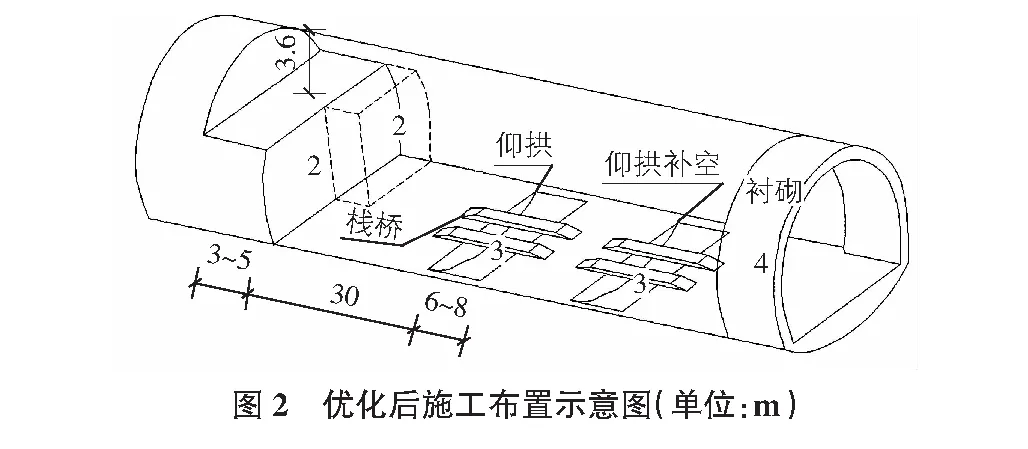
对太岳山隧道优化后施工方案的初步分析可知，在调整上下台阶的开挖高度后，由于上台阶断面缩小，上台阶初期支护工作量将变小，支护时间缩短，且台阶开挖高度调整后，安全步长关系将更容易保证。

4 数值模拟分析

4.1 计算模型和计算参数

为评估太岳山隧道的施工优化方案，分别建立隧道施工方案优化前后两个计算模型。其中，两计算模型沿水平X方向长度均为210 m；竖直Z方向的长度均为220 m；优化前计算模型沿洞轴Y方向的长度为100 m，优化后计算模型沿洞轴Y方向的长度为90 m。优化前的计算模型包含334 106个单元，56 783个节点；优化后的计算模型包含207 407个单元，35 434个节点。隧道横截面具体尺寸如图3所示。模型四周竖直面和底部均采用垂直约束，顶部采用自由边界条件。前期勘查工作表明，隧道开挖区域地应力以自重应力为主，隧道围岩容重约为27.7 kN/m3。

计算时采用Mohr-Coulomb屈服准则。计算参数将以围岩变形实际监测值为基础，采用参数反演方法[8]得到。太岳山隧道围岩变形监测位置见图3，由图可知，隧道横截面上布置有3个位移监测点，其中，监测点1监测拱顶的下沉变形量，监测点2和3监测水平方向围岩的收敛位移。通过实测得到太岳山隧道围岩的拱顶累计下沉变形量在12 mm左右，水平向围岩的收敛位移在47.5 mm左右。由此反演得到的计算参数见表1。

表1 计算参数的取值

4.2 计算结果分析

通过对太岳山隧道施工方案优化前后两种工况进行计算，得到了不同工况下围岩的变形计算结果(见图4)。由图4a)可知，优化前，由于上台阶较长(20 m左右)，上台阶开挖后因拱顶围岩松弛导致下沉变形较大，最大累计下沉量达18 mm；此外，在隧底和台阶处围岩变形亦较大。优化后隧道围岩位移场计算结果见图4b)，由图可知，与优化前相比，优化后上台阶明显变短(5 m左右)，上台阶开挖后拱顶的下沉变形也明显变小(8 mm左右)，隧道开挖完成后，拱顶围岩的最终变形量也较优化前减小了约2 mm(累计下沉量16 mm左右)。

4.3 优化前后的施工情况对比

实际的施工情况也表明，调整台阶高度后，由于上台阶断面缩小，上台阶初期支护工作量变小，支护时间缩短，顶部水平岩层坍塌情况有所缓解；且台阶调整后，安全步长关系更容易保证，上下台阶共同推进，施工进度稳步加快。

此处，将优化前后的施工情况进行了对比(见表2)。由表2可知，优化后，上台阶开挖及出碴时间由优化前的4.5 h缩短为2.5 h；初期支护时间由优化前的3.5 h缩短为2 h；且台阶调整后，上下台阶共同推进，步长关系易保证，开挖支护月平均进度由120 m提高到180 m，最高月进度创210 m好成绩。

表2 台阶优化前后施工情况对比

5 结语

针对太岳山隧道在施工过程中所遇到的问题，本文对其施工方案进行了优化，并对优化前后的施工方案进行了数值模拟对比分析。最后，结合数值计算结果和现场实际情况对优化后施工方案的合理性进行了评价。主要包括如下内容：

1)太岳山隧道施工初期按照传统的双线隧道台阶法开展施工，施工过程出现了顶部岩层掉块垮塌、台阶法步长关系不协调以及台阶高度与格栅钢架高度不匹配等不利的工程情况，本文针对上述问题，提出了施工优化方案。2)通过对优化前后的施工方案进行数值模拟对比可知，相对于优化前，太岳山隧道施工方案优化后的拱顶下沉变形量明显减小，围岩稳定性增强。3)实际施工情况表明，施工方案优化后，由于上台阶断面缩小，上台阶初期支护工作量变小，支护时间缩短，顶部水平岩层坍塌情况有所缓解；且台阶调整后，安全步长关系更容易保证，上下台阶共同推进，施工进度稳步加快。

本文针对太岳山隧道施工方案优化而开展的研究工作，对我国类似工程的设计和施工具有参考和借鉴的意义。

[1] 郭陕云.论我国隧道和地下工程技术的研究和发展[J].隧道建设，2004,25(4):19-20.

[2] 张云峰.隧道施工过程的数值模拟分析与方案研究[D].合肥：合肥工业大学，2007.

[3] 李术才,王汉鹏,郑学芬.分岔隧道稳定性分析及施工优化研究[J].岩石力学与工程学报,2008,27(3):447-457.

[4] 胡世权.龙潭隧道页岩段施工优化数值模拟[J].土工基础,2012,26(2):42-46.

[5] 杨凡杰，周 辉，肖海斌，等.大理岩弹性参数的围压效应与弹塑性耦合模型[J].岩土力学,2013,34(6):1613-1620.

[6] 赵玉光，张焕新，林志远，等.双连拱隧道施工力学数值模拟与施工方法比选[J].广西交通科技,2003,28(4):25-30.

[7] 佘 健，何 川.软弱围岩段隧道施工过程中围岩位移的三维弹塑性数值模拟[J].岩石力学与工程学报,2006,25(3):623-629.

[8] 陈炳瑞，冯夏庭，黄书岭，等.基于快速拉格朗日分析—并行粒子群算法的黏弹塑性参数反演及其应用[J].岩石力学与工程学报,2007,26(12):2517-2525.

Analysis on construction optimization and numerical simulation of Taiyueshan tunnel

Song Li

(ChinaRailway3rdBureauGroupCo.,Ltd,Taiyuan030001,China)

In light of Taiyueshan tunnel construction problems including top rock collapse, incoordination benching tunneling method, and mismatching of benching height and grid height, the paper puts forward construction optimizing scheme, simulates and analyzes construction scheme before and after optimization with numerical calculation method. Results show that: optimized construction scheme effectively guarantees the tunnel construction quality and construction schedule.

tunnel engineering, mudstone, benching tunneling method, construction optimization, numerical analysis

2014-12-13

宋 力(1982- )，男，硕士，工程师

1009-6825(2015)06-0163-03

U455

A