基于城市经济空间联系的江西省区域发展研究

廖汉鲁， 刘亚平

(华东交通大学 经济管理学院，江西 南昌 330013)

基于城市经济空间联系的江西省区域发展研究

廖汉鲁， 刘亚平

(华东交通大学 经济管理学院，江西 南昌 330013)

区域经济空间联系是经济地理学和区域研究的重要内容。利用引力模型，以江西省为例，分析了省内11个地级市的经济联系强度。结果表明：江西省各城市的发展状况差距较大，区域经济发展水平出现较明显的不平衡，经济联系呈现出以南昌为中心向外依次减弱的趋势，外围城市之间经济联系度不高。最后根据实证结果提出了加强江西省城市经济联系和优化区域发展的若干政策建议。

江西省；引力模型；城市质量；城市经济空间联系；经济联系强度；区域发展

一、引言

在经济全球化与区域经济一体化进程不断加快的背景下，区域经济空间联系和相互作用成为经济地理学和区域研究的重要内容，而城市之间的经济联系则吸引越来越多学者的关注和研究。研究城市间的经济联系，是测度区域经济活跃程度和一体化进程的重要依据，同时也为正确地制定经济发展战略提供可靠保证，对于城市之间区域规划与统筹区域经济发展具有重要意义。

国外在区域经济联系方面的研究较早，赖利(W.J.Reilly,1929)根据牛顿力学万有引力模型提出了“零售引力定律”，总结出都市人口与零售引力之间的关系，为定量分析区域空间联系奠定了理论基础[1]，齐夫(G.K.Zipf，1942)将万有引力定律引入城市体系，对城市间空间相互作用进行分析，建立了城市群空间相互作用的理论基础[2]，康弗斯 (P.D.Converse，1949)进一步发展了Reilly的理论，提出了断裂点的概念和计算公式[3]，哈里斯( C.D.Harris，1943)将人均批发销售额和人均零售额作为测量中心性的标准，来确定城市有无对外联系[4]。乌尔曼(E.L.Ullman，1957)提出了空间相互作用理论，并指出空间相互作用的三个基本原则：互补性、移动性和中介机会，对城市体系空间相互作用机制研究影响深远[5]。

国内学者对区域经济空间联系研究较晚，主要在20世纪90年代以后，运用一些指标、模型或方法对区域经济联系进行实证研究，如姜博(2009)、 陈群元等(2011)采用从业人员、GDP、人均GDP等指标，运用城市流强度模型测算环渤海地区三大城市群、环长株潭城市群的城市流强度值，分析城市间的空间联系[6-7]。孟德友(2009)、 李红锦(2011)采用GDP总量、人口数量、交通距离等指标，运用引力模型测算江苏省、珠三角城市群的经济联系强度[8-9]。郑良海等(2011)、贾卓等(2013)则在GDP、非农业人口之外，加入研究技术人员数、固定资产投资、具有大学( 指大专及以上) 教育程度的人口数量和全社会消费品零售额等指标，运用中心职能指数、交通可达性系数以及引力模型，对关中城市群、兰白西城市群区域各城市间的经济联系行了测定和分析[10-11]。张建营等(2012)运用改进的引力模型，从经济综合实力、经济发展支持力、城市开放程度、城市规模影响力四个层面采取指标，利用城市发展质量对珠三角城市群的经济空间联系进行了定量分析[12]。刘健朝等(2013)从区域和产业两个角度，采用经济联系强度模型和城市流模型对京津冀城市群空间联系和经济联系进行了实证研究[13]。

然而，这些研究大部分都集中在经济较为发达、城市联系较为密切的地区，对城市发展水平较低、内部联系相对松散的地区研究较少。另外以单一指标或简单几个指标作为城市质量的度量方法存在较大的缺陷。因为区域发展是由资金、基础设施、对外联系、科学技术等多种因素决定的，单一或少数几个指标无法完全反映区域经济发展的全貌。江西省位于我国中部地区，紧邻长三角、珠三角和海西经济区，从区位上来说，具有承接这些地区产业转移的得天独厚的区位优势。但是由于经济基础不高，区内经济联系不密切，使得江西省经济区域发展质量一直处于中部地区的后位。因此，本文以江西省为例，运用引力模型，对江西省11个城市的经济空间联系进行实证分析，以期加强江西省城市间的经济联系，优化区域发展战略，提高江西省的区域竞争力。

二、引力模型的构建

作为经济区的核心和重心，同时也是增长极的城市对周围地区有较强的吸引力和辐射力。通常把城市间的相互引力作为衡量影响城市间经济联系紧密程度的一个重要因素，同时也把它作为经济区划的重要依据。本研究基于由空间相互作用原理产生的引力模型来量化计算城市经济空间联系强度，它是根据距离衰减原理和牛顿万有引力定律构造出来的一个模型，其公式为[14]：

(1)

式中:Pi、Pj分别为i、j城市的总人口；Gi、Gj分别为i、j城市的经济规模(用GDP总量衡量)；Dij为i、j城市之间的交通距离；Rij为i、j城市间的经济联系强度。引力模型只考虑了影响空间相互作用的少数因子，仅能粗略地估算区域间的空间相互作用力，即以人口和GDP作为城市质量的度量方法显然存在较大的缺陷，无法完全反映城市经济发展的全貌，因为城市发展程度是由多种因素相互影响综合决定的。事实上，目前许多研究中已经注意到区域综合发展质量评定的重要性，本文通过建立一套完善的指标体系来反映城市的综合发展质量。此外，对模型建立过程中城市间距离问题的确定，起初很多学者简单地使用直线距离，但随着道路网络以及现代交通工具的发展，简单地采用两点间的直线距离为标准，就会出现较大的局限性。因为在交通便捷的地方，道路直线距离已不具备可比性，因此本文用两地间到达的最短的时间距离进行代替。

根据上述分析，将引力模型式(1)修正为

(2)

式中，Rij代表两个区域间的空间经济吸引力；Mi、Mj分别表示区域 i 和区域 j 的“质量”，代替人们常用的人口与 GDP 的乘积来衡量区域城市发展的质量；Dij表示两区域间到达的最短时间距离，本文采用google地图软件测度两城市间的时间距离；k为经济引力系数，为简便起见，本文取k=1。

本文借鉴已有参考文献有关城市发展质量以及城市竞争力评价的相关指标[15-17]，以综合反映一个城市的发展水平为原则，将城市发展质量评价指标体系划分为综合经济实力、基础设施水平、对外开放程度、科技教育水平等4个维度和24个指标(见表1) 。

表1 江西省城市综合质量评价指标体系

三、城市经济空间联系的实证分析

根据构建的城市质量评价指标体系，选取江西省2012年的指标数据为分析对象。指标数据主要来源于《江西统计年鉴2013》，部分指标数据经过整理而得。采用主成分分析法对数据进行分析。

(一)城市质量主成分分析

主成分分析是利用降维的思想，在尽可能地保留原始数据信息的情况下，把多个指标转化为少数几个综合指标的一种多变量数据进行最佳综合简化的多元统计方法。一般步骤包括:数据标准化后计算其R阵、R阵的特征根和特征向量、根据主成分贡献率确定主成分个数，最后合成计算各主成分得到综合评价值。

利用 SPSS软件对所选择的原始数据进行处理，得到综合经济实力、基础设施水平、对外开放程度、科技教育水平各评价维度的主成分分析结果，见表2。

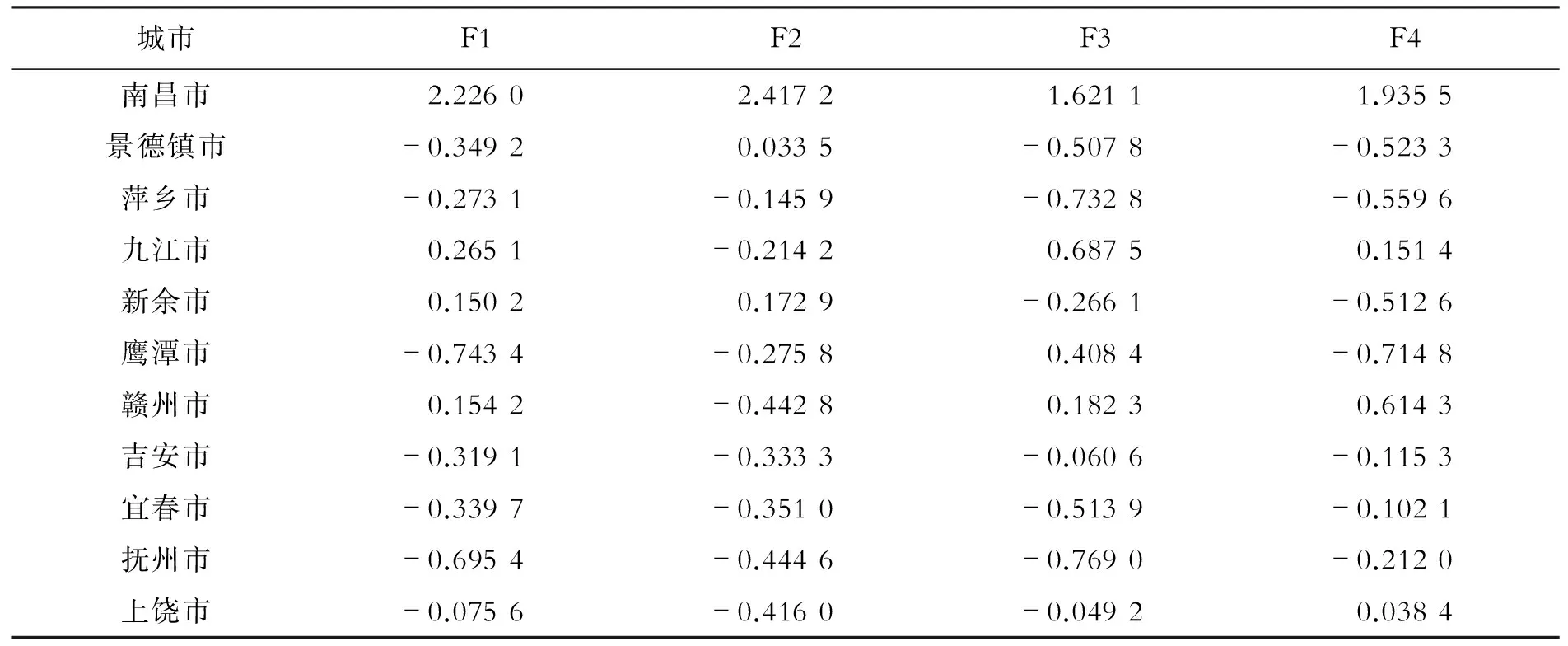
表2 江西省各城市质量评价维度的综合得分

通过SPSS分析软件的因子分析功能对表2的数据进行标准化处理，得到特征值及方差贡献率矩阵，见表3。

如表3所示，方差贡献率累计是85.920%，根据累计贡献率需大于 85% 的原则，提取第一主成分F作为新的变量指标来计算各城市的综合发展实力。由此，计算出江西省各个城市的城市质量，见表4 。

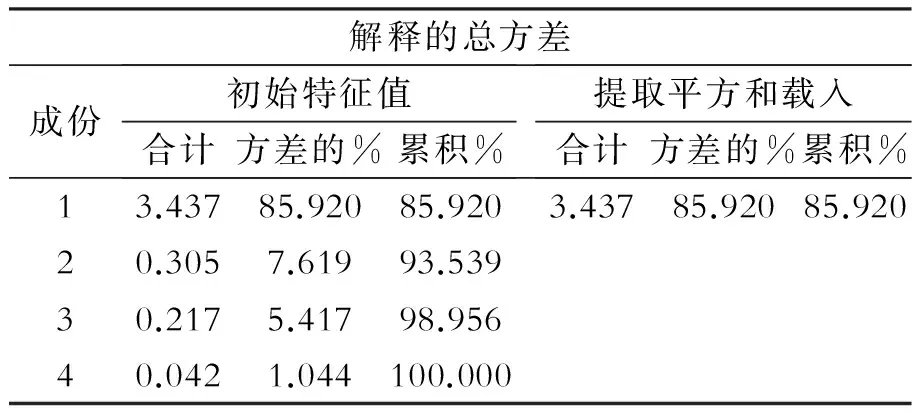
表3 方差贡献率矩阵

提取方法：主成分分析。

表4 江西省各城市质量

注：由于综合得分计算结果出现负值，不利于下文计算，因此在综合得分的基础上进行修正[18]。

(二)江西省城市联系度的测算

基于数据的可获得性，本文根据Google地图搜索得出城市间到达的最短时间距离，见表5。

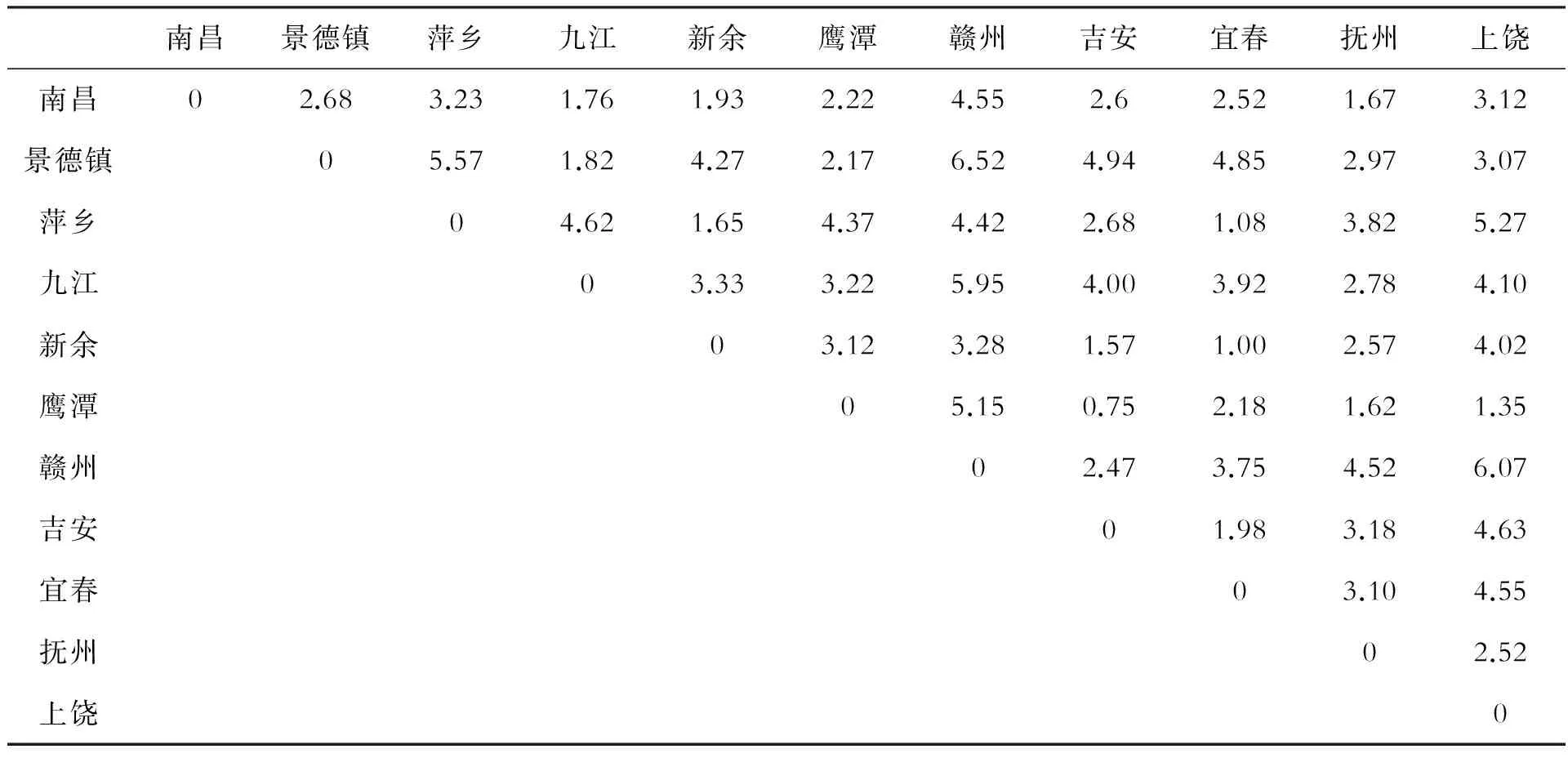
表5 江西省各城市间的时间距离 单位：小时

利用表 4、表 5 的数据，根据公式(2) 计算江西省各城市间的联系度，见表6。

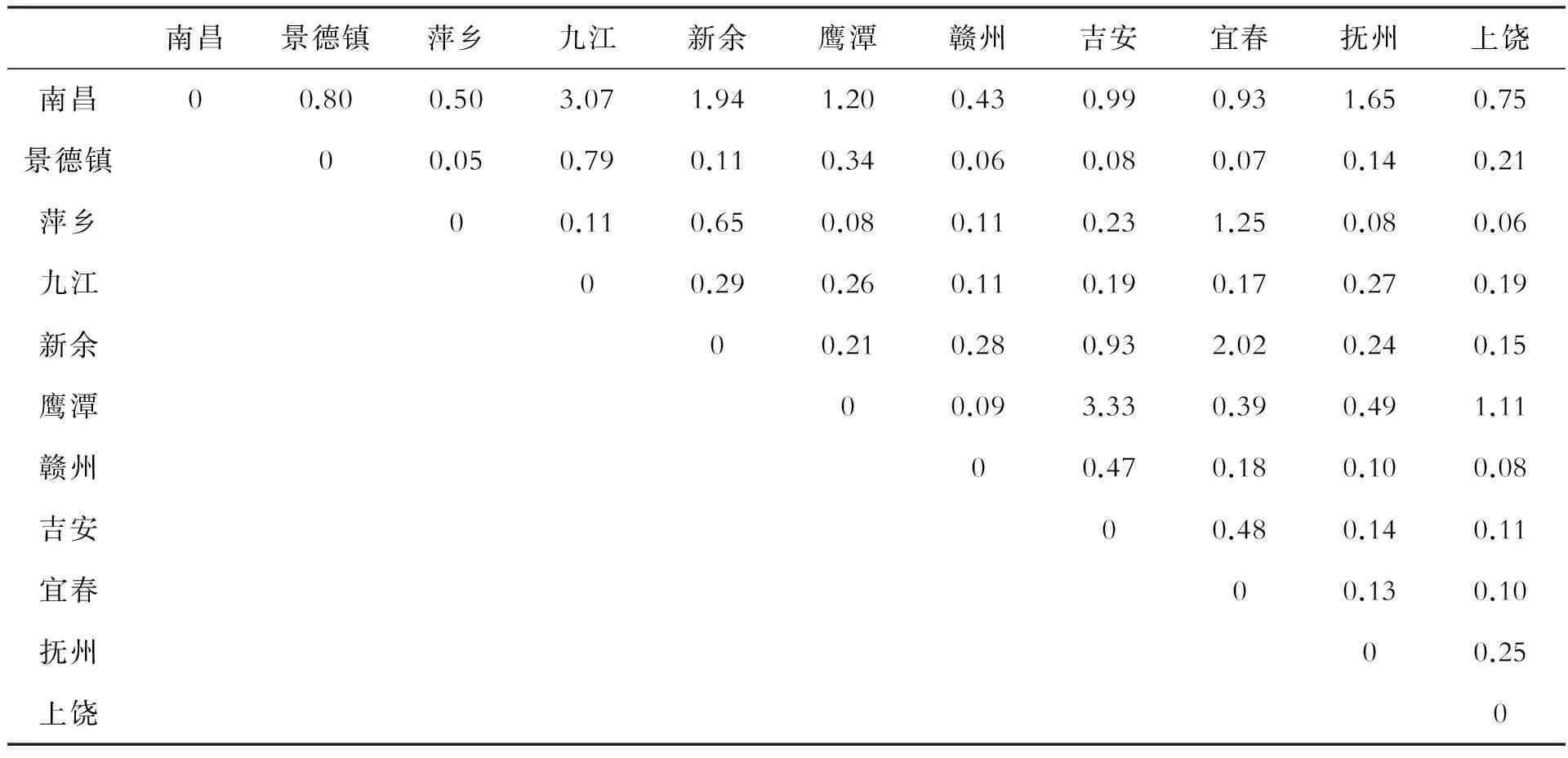
表6 江西省各城市间的联系度

(三)结果分析

从城市质量计算结果(表4)可以看出，江西省区域内不同城市的发展状况差距较大，表现出较明显的区域经济发展的不平衡。城市群中的要素基本流向了南昌市、九江市和赣州市，它们的城市发展水平明显高于区内其他城市，其中以南昌最为明显。另外与前人简单以人口和GDP等指标进行测量相比，从综合经济实力、基础设施水平、对外开放程度、科技教育水平等多方面采取指标进行测量，其结果更加全面和准确，更加真实反映了江西省各地区的发展水平。从城市经济联系结果(表6)中可以看出，以南昌作为核心城市而言，其对九江、抚州、新余、鹰潭的吸引力最大，这几个城市可以被看成一个以南昌为首的鄱阳湖生态城市群。作为赣南的赣州，其城市经济发展水平相对来说较高，但是它对其他城市的辐射带动作用却很有限，仅对周边城市吉安有较大的吸引力，而对其他城市的带动作用不大。处于赣西的宜春、萍乡、新余三市联系比较紧密，但是城市质量总体发展水平不高，因此对其他城市的辐射作用也较为有限。从城市经济联系结果也可看出，以时间距离来代替直线距离，更能反映当前的交通发展现状，其结果也更加直观[21]。

四、结论与对策建议

2011年10月，江西省第十三次党代会提出构建“龙头昂起、两翼齐飞、苏区振兴、绿色崛起”的区域发展格局。为打造区域经济增长极，实现江西在中部崛起战略，江西省依托鄱阳湖生态经济区建设和赣南等原中央苏区振兴发展两大国家战略，大力构建多极支撑、多元发展的区域发展升级新格局。 然而，本文的实证分析结果表明，虽然江西省依托两大国家战略取得了一定的发展，但是江西省区域内发展不平衡的问题仍然比较突出，以南昌为中心，呈现出明显的中心外围空间结构，外围城市间的经济联系仍然不够紧密，区域内经济的协调发展和一体化进程还有待进一步加强。为进一步完善江西省的区域发展格局，增强城市间经济空间联系，本文提出以下政策建议：

(一)加快推动昌九一体化建设

南昌与九江城市发展在全省处于领先水平，要实现龙头昂起，进一步推动鄱阳湖生态经济区的发展，必须要做强南昌，做大九江，加快推进昌九一体化建设，加强中心城市的辐射带动能力。一方面要重点推进打造南昌核心增长极，南昌市作为江西省的政治、经济、文化、基础研究与高等教育中心，其经济发展质量以及与其他城市的经济联系度都较高，所以应积极打造南昌核心增长极。积极推进南昌大都市区建设，加快形成南昌一小时经济圈，充分发挥南昌对省内其他城市的辐射带动作用，促进区域经济的协调发展。另一方面，作为与南昌经济联系强度最高的九江，应积极推进九江沿江开放开发，充分发挥门户城市的区位优势，加快临港产业开发，积极发展商贸旅游业，把九江建成具有鲜明赣文化特色的赣北区域中心城市、现代化港口旅游城市、区域性物流枢纽和长江沿岸重要工业基地。总的来说，要推动昌九一体化发展，两地应进行规划统筹，实现规划上的一体化；在基础设施建设上进行接轨，实现基础设施一体化；按照各自的产业特色和产业结构推动双方产业调整，实现产业的互补对接、积极推进金融、通讯、公共交通一体化；实现服务一体化，最终实现昌九同城效应。

(二)积极支持赣东、赣西区域发展

从城市发展质量和联系度来说，赣东、赣西地区城市整体发展水平不高，城市之间联系不够紧密。所以应以沪昆线为驱动轴，加强政府规划引导和政策支持，优化两翼的区域生产力布局。具体来说，应根据两翼地区的区位条件、产业基础、资源禀赋来推动各个区域的发展。处于赣东地区的鹰潭市可依托龙虎山这一世界自然遗产优势，打造文化旅游城市；另外国内最大、世界第三的江铜冶炼基地落户鹰潭有利于该地区打造“世界铜都”和相关产业的物流节点；上饶市光伏、光学、先进装备制造业相较于江西其他地区基础比较好，可以发展成江西整个地区发展这些产业的基地；景德镇市作为“世界瓷都”享誉海内外，依托该产业可以进一步发展瓷文化旅游观光等等。另外，应加快推进昌抚一体化进程，推动抚州的发展，同时实现南昌乃至江西省与海西经济区的无缝对接，承接东部发达省份的产业转移，享受国家支持海西经济区建设的政策溢出效应。对于赣西地区，从萍乡、新余、宜春三市的经济联系度可以看出，三市的经济联系较为紧密。应推进新余、宜春、萍乡的城镇规划、基础设施、公共服务同城化发展，加快打造钢铁、新能源、新材料、锂电、生物医药等产业集聚区，逐步形成一批特色优势产业板块，另外拓宽西部城市与长株潭城市群的合作对接，真正实现两翼齐飞，促进江西省内的均衡发展。

(三)大力推进赣南等原中央苏区的发展

从城市发展质量来说，赣州市的综合发展质量仅次于南昌和九江，所以应进一步巩固赣州的次中心城市地位，形成“九昌赣”城市发展纵向核心轴线，带动全省经济发展。具体来说，应把赣州打造成赣粤闽湘4省通衢的区域性现代化中心城市和区域性综合交通枢纽，并根据赣州的产业特点把赣州发展成为全国重要的钨产业、稀土产业、氟盐化工基地和世界最大的优质脐橙生产基地，最终把赣州建设成为对赣南地区以及周边城市具有较强带动功能的区域性中心城市。与赣州联系最紧密的吉安则应加强与赣州之间的经济往来，吸收并依托吉泰走廊，重点建设电子信息产业基地和全国红色旅游精品城市，与赣州一起形成都市圈，加快赣南等原中央苏区的振兴发展。

[1]Reilly W J.Methods for the study of retail relationships[M].University of Texas，Bulletin (2944)，1929：1-91.

[2]李俊峰,焦华富.江淮城市群空间联系及整合模式[J].地理研究,2010(3):535-544.

[3]Converse P D.New laws of retail gravitation[J].Journal of Marketing，1949,14:379-384

[4]Harris C D.A Functional Classification of Cities in the United States[J].Geographical Review，1943(33):86-99

[5]Ullman E L.American Commodity Flow[M].Seattle:University of Washington Press，1957：60-73.

[6]姜博,修春亮,赵映慧.“十五”时期环渤海城市群经济联系分析[J].地理科学,2009(3):347-352.

[7]陈群元,宋玉祥.基于城市流视角的环长株潭城市群空间联系分析[J].经济地理,2011(11):1840-1844.

[8]孟德友,陆玉麒.基于引力模型的江苏区域经济联系强度与方向[J].地理科学进展,2009(5):697-704.

[9]李红锦,李胜会.基于引力模型的城市群经济空间联系研究——珠三角城市群的实证研究[J].华南理工大学学报：社会科学版,2011(1):19-24.

[10]郑良海,邓晓兰,侯英.基于引力模型的关中城市间联系测度分析[J].人文地理,2011(2):80-84+107.

[11]贾卓,陈兴鹏,袁媛.中国西部城市群城市间联系测度与功能升级研究——以兰白西城市群为例[J].城市发展研究,2013(4):71-76.

[12]张建营,毛艳华.珠三角城市群经济空间联系实证分析[J].城市问题,2012(10):2-8.

[13]刘建朝,高素英.基于城市联系强度与城市流的京津冀城市群空间联系研究[J].地域研究与开发,2013,02:57-61.

[14]许学强，周一星，宁越敏.城市地理学[M].北京：高等教育出版社，2003：150-154.

[15]王发曾,吕嵘.中原城市群城市竞争力的评价与时空演变[J].地理研究,2011(1):49-60.

[16]倪鹏飞,刘高军,宋璇涛.中国城市竞争力聚类分析[J].中国工业经济,2003(7):34-39.

[17]王成新,李新华,王格芳,等.城市群竞争力评价实证研究——以山东半岛城市群为例[J].地域研究与开发,2012(5):50-54.

[18]王学定,范宪伟,高峰.基于城市联系的甘肃省区域发展战略[J].城市问题,2012(5):72-76.

[19]赵林,韩增林,马慧强.中原经济区城市内在经济联系分析[J].经济地理,2012(3):57-62+8.

[20]段七零,毛建明.基于引力模型与0-1规划模型的省域经济区划——以江苏省为例[J].经济地理,2011(8):1239-1245.

[21]王海龙,朱洪兴.京津冀地区的城市引力研究[J].企业经济,2010(3):97-100.

Research on Regional Development in Jiangxi Province Based on Urban Economic Space Linkage

LIAO Han-lu, LIU Ya-ping

(School of Economic and Management, East China Jiaotong University, Nanchang 330013, china)

Regional economic space linkage is one of the important contents in economic geography and regional research.By using gravity model, taking Jiangxi province as an example, this paper analyzes the intensity of economic linkage among 11 prefecture-level cities in Jiangxi province.The results show that there is a big gap among the cities in Jiangxi province in current situation of development; the development level of regional economic is obviously imbalanced; the economic linkage presents a trend like Nanchang as the center weakened outward successively; the intensity of the economic linkage among the outside cities is lower.Finally, some policy suggestions are put forward to strengthen the economic linkage among cities in Jiangxi province and optimize original development.

Jiangxi province; gravity model; urban quality; urban economic space linkage; intensity of economic linkage; original development

2095-0365(2015)01-0006-06

2014-07-26

廖汉鲁(1967-)，男，副教授，博士，研究方向：企业管理、战略管理。

A

10.13319/j.cnki.sjztddxxbskb.2015.01.02

本文信息:廖汉鲁，刘亚平.基于城市经济空间联系的江西省区域发展研究[J].石家庄铁道大学学报：社会科学版，2015，9(1)：6-11.