RANSAC估算基础矩阵的不确定性评价

卞 玉 霞,刘 学 军,刘 丹

(南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210023)



RANSAC估算基础矩阵的不确定性评价

卞 玉 霞,刘 学 军,刘 丹

(南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210023)

RANSAC是计算机视觉领域内应用最广泛的基础矩阵估算方法，如何实现RANSAC估算基础矩阵的不确定性评价值得探讨。该文在研究RANSAC估算基础矩阵模型的基础上，提出采用基础矩阵的错误率和平均对极距离的标准差作为评价RANSAC估算基础矩阵不确定性的指标，并构建RANSAC估算基础矩阵不确定性评价方法，实现RANSAC估算基础矩阵不确定性评价。

RANSAC;基础矩阵;错误率;平均对极距离;标准差

0 引言

基础矩阵是序列图像三维建模技术的核心命题之一，其不确定性直接影响摄像机标定、三维点云恢复等序列图像三维建模后续环节的参数精度。现有的估算基础矩阵方法主要有：线性方法[1,2]、迭代方法[3]和鲁棒方法。考虑到线性和迭代方法不适用于存在错误匹配点的情况，目前序列图像三维重建中主要采用鲁棒方法估计基础矩阵。在最小平方中值法[4,5]、M-estimators方法[6,7]、随机抽样一致算法(Random Sample Consensus，RANSAC)[8-11]等众多的鲁棒方法中，RANSAC是计算机视觉领域内应用最广泛的[9]，是存在错误匹配点时较合适、常用的估算基础矩阵的鲁棒方法。

在RANSAC估算基础矩阵不确定性研究方面，有学者针对GUM(Guide to the expression of Uncertainty in Measurement)方法评估基础矩阵的不确定性，如：基于协方差矩阵表达基础矩阵的不确定性[12,13]、采用八点线性算法估算基础矩阵的不确定性[14]等。Silva等[15]认为“目前不确定性主要基于GUM方法进行评估，今后可以用蒙特卡罗方法进行不确定性评估”。蒙特卡罗模拟RANSAC估算基础矩阵不确定性研究中，如何实现RANSAC估算基础矩阵的不确定性评价是一个值得研究的问题。

为了解决上述问题，本文在研究RANSAC估算基础矩阵模型基础上，提出RANSAC估算基础矩阵不确定性的评价指标，并构建RANSAC估算基础矩阵不确定性评价方法，最后通过实验方法实现RANSAC估算基础矩阵不确定性评价。

1 RANSAC估算基础矩阵

RANSAC是计算机视觉中关于鲁棒参数估计的一种典型方法，它最早被Torr用于基础矩阵估计。RANSAC估算基础矩阵的主要思想是随机选取最小样本子集，计算该样本子集得到初始基础矩阵，并进一步判断该初始基础矩阵条件下一定距离阈值内所包含的数据点集，重复随机采样，最后选取最大的数据点集估算基础矩阵，该值即作为RANSAC估算基础矩阵的最终结果。

为了实现基础矩阵模型与含有野值的鲁棒拟合，本文研究Silva的RANSAC估算基础矩阵模型及开源程序库，该过程实质上可以看做是模型假设和验证的过程。如图1所示，具体的工作流程为：1)从样本集S中随机选择7个匹配点对作为最小样本子集，采用7点线性算法估算初始基础矩阵F1。2)确定与F1相关的距离阈值内所包含的数据点集。3)重复步骤1和2，确定N次采样中与各个初始基础矩阵相关的距离阈值内所包含的数据点集。4)从步骤3中选择最大的数据点集，并采用最小二乘原理计算基础矩阵，该值即作为RANSAC估算基础矩阵的最终结果。

2 RANSAC估算基础矩阵的不确定性

本文拟采用基础矩阵的错误率和平均对极距离的标准差作为基础矩阵不确定性的评价指标，并构建RANSAC估算基础矩阵不确定性的评价方法。

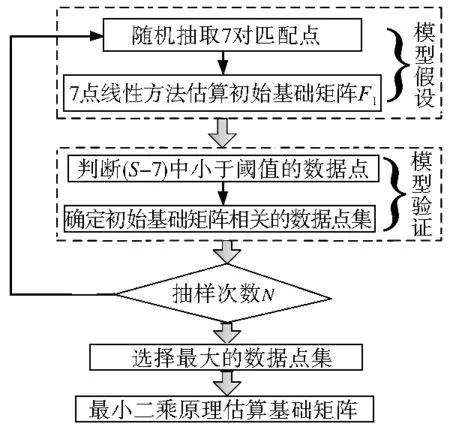
图1 RANSAC估算基础矩阵

Fig.1 The estimation of fundamental matrix based on RANSAC

2.1 评价指标

基础矩阵的错误率和平均对极距离的残差是基于平均对极距离进行量化的。平均对极距离是立体像对中所包含的每一匹配点的对极线与该点在另一幅图像上的匹配点之间的距离(对匹配中的两点都计算)平方和的均值U。如图2所示，U具体表达为[16]：

(1)

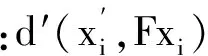
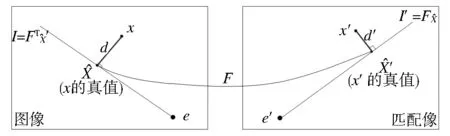
图2 点到相应对极线的距离

Fig.2Thedistancebetweenmatchpointandcorrespondingepipolarline

(1)基础矩阵的错误率。RANSAC估算基础矩阵是采用随机抽样法抽取样本进行估算的，其计算过程具有随机性，特别是当最大数据点集中包含野值时，估算的基础矩阵会存在错误基础矩阵。估算基础矩阵正确与否可以作为评价基础矩阵不确定性的指标之一。

基于式(1)，将平均对极距离较大时的基础矩阵定义为错误基础矩阵。采用统计学原理分析RANSAC估算基础矩阵不确定性时，基础矩阵的错误率Err可以表示为：

(2)

式中：e表示平均对极距离较大时的基础矩阵数量；M表示模拟次数。

(2)平均对极距离的标准差。不同矩阵之间不存在均值和方差等统计意义，基础矩阵线性化是实现基础矩阵不确定性统计分析的方法之一。已知基础矩阵，可以计算匹配点到相应对极线的距离，该值是由于匹配点位置不确定性引起的。当已知匹配点位置，可以计算匹配点到相应对极线的距离，该值是由于基础矩阵的不确定性引起的。基于这样的思考，本文将评价基础矩阵不确定性转化为求平均对极距离U的标准差(σU)，公式为：

(3)

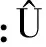
2.2 评价方法

在统计学中，不确定性主要包含误差和粗差。本文假设基础矩阵的错误率相当于统计学中的粗差，而平均对极距离的标准差相当于统计学中的误差，它们共同表达了RANSAC估算基础矩阵的不确定性。结合RANSAC估算基础矩阵模型，本文在选用基础矩阵的错误率和平均对极距离的残差这两个评价指标的基础上，设计了图3所示的RANSAC估算基础矩阵不确定性的评价方法。

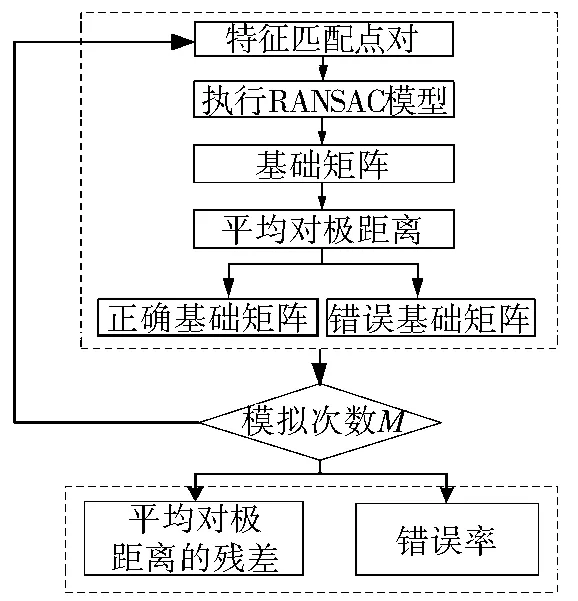
图3 RANSAC估算基础矩阵的不确定性评价方法

RANSAC估算基础矩阵的不确定性评价方法是基于立体像对中提取的匹配点对，通过执行RANSAC模型获得基础矩阵的条件下，根据式(1)计算立体像对中提取的匹配点对的平均对极距离，进而判断与该平均对极距离相对应的基础矩阵是错误基础矩阵还是正确基础矩阵。当执行M次模拟后，统计错误基础矩阵的数量，进而根据式(2)计算基础矩阵的错误率,并根据式(3)计算正确基础矩阵所对应的平均对极距离的标准差。

3 实验分析

为了实现基于基础矩阵的错误率和平均对极距离的标准差来评价RANSAC估算基础矩阵不确定性，本实验选用RANSAC开源程序库中的立体像对，用SIFT特征匹配模型提取的匹配点对作为本实验的数据源。如图4所示，图中线段的两端点表示提取的匹配点对。

图4 数据源

Fig.4 The data source

本次实验设M=1 000，执行如图3所示的RANSAC估算基础矩阵的不确定性评价方法，其结果如图5所示。图5中横坐标是模拟次数M，纵坐标是每次模拟所计算的平均对极距离，可以看出，平均对极距离主要分布在0～1和80～140等区域。显然，80～140区域中平均对极距离过大，这是由于RANSAC估算基础矩阵错误而引起的。文献[17]中指出大多数匹配点的误差会控制在3个像素以内，因此本实验规定基础矩阵的错误率是平均对极距离大于3个像素的基础矩阵与M的比值。

图5中有149个平均对极距离大于3，即有149个错误基础矩阵，根据式(2)可以认为本实验中RANSAC估算基础矩阵的错误率为15%。当剔除149个错误基础矩阵时，图5中有851个正确基础矩阵，根据式(3)统计分析可以得出：正确基础矩阵对应的平均对极距离为0.31，标准差为0.001。图5中的局部放大图展示的是第3～23次的模拟结果，它代表与正确基础矩阵相对应的平均对极距离的分布情况，图中各平均对极距离及其变化趋势清晰地表明上述计算平均距离标准差的正确性。

图5 平均对极距离

Fig.5 The mean distance of epipolar

4 结论

立体像对中提取的匹配点对存在正确匹配点对和错误匹配点对，其作为RANSAC估算基础矩阵的数据源时，会影响RANSAC估算基础矩阵结果的正确性；且RANSAC估算基础矩阵的结果是矩阵的形式，它不具备统计意义。为了解决以上问题，本文提出用基础矩阵的错误率和平均对极距离的标准差作为评价RANSAC估算基础矩阵不确定性的指标，并在此基础上构建了RANSAC估算基础矩阵不确定性评价方法，实现了RANSAC估算基础矩阵不确定性的评价。

[1] HARTLEY R.Projective reconstruction from line correspondence[A].Computer Vision and Pattern Recognition[C].1994.

[2] LONGUET H C.A computer algorithm for reconstructing a scene from two projections[J].Nature,1981,293(10):133-135.

[3] LUONG Q T,FAUGERAS O D.Determining the fundamental matrix with planes:Unstability and new algorithm[A].Computer Vision and Pattern Recognition[C].1993.489-494.

[4] ROUSSEEUW P,LEROY A.Robust Regression and Outlier Detection[M].New York：John Wiley & Sons,1987.

[5] ZHOU H,GREEN P R,WALLACE A M.Estimating of epipolar geometry by linear mixed-effect modeling[J].Neurocomputing,2009,72(6):3881-3890.

[6] HUBER P J.Robust Statistics[M].New York:John Wiley & Sons,1981.

[7] 张洁玉,陈强,刘复昌,等.一种改进的M-Estimators基础矩阵鲁棒估计法[J].中国图象图形学报，2009,14(8):1663-1668.

[8] FISCHLER M,BOLLES R.Random sample consensus:A paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM,1981,24:381-385.

[9] 陈付幸,王润生.基于预检验的快速随机抽样一致性算法[J].软件学报,2005,16(8):1431-1437.

[10] 田文,王宏远,徐帆,等.RANSAC算法的自适应Tc,d预检验[J].中国图象图形学报,2009,14(5):973-977.

[11] 周骏.陈雷霆.刘启,等.基于序贯概率及局部优化随机抽样一致性算法[J].仪器仪表学报,2012,33(9):2037-2044.

[12] CSURKA G,ZELLER C,ZHANG Z,et al.Characterizing the uncertainty of the fundamental matrix[J].Computer Vision and Image Understanding,1997,68(1):18-36.

[13] RAGURAM R,FRAHM J M,POLLEFEYS M.Exploiting uncertainty in random sample consensus[A].Computer Vision[C].2009.2074-2081.

[14] SUR F,NOURY N,BERGER M O.Computing the uncertainty of the 8 point algorithm for fundamental matrix estimation[C].BMVC,2008.

[15] SILVA H P,CATEN C S.Measurement uncertainty:Literature review and research trends[J].Instrumentation and Measurement,2012,61(8):2116-2124.

[16] 韦穗,杨尚骏,章权冰,等.计算机视觉中的多视图几何[M].合肥:安徽大学出版社,2002.198-199.

[17] 钟慧湘.基础矩阵计算方法的研究[D].吉林:吉林大学,2005.32-33.

Estimation of Fundamental Matrix Uncertainty Based on Random Sample Consensus

BIAN Yu-xia，LIU Xue-jun，LIU Dan

(KeyLaboratoryofVirtualGeographicEnvironment(NanjingNormalUniversity),MinistryofEducation,Nanjing210023,China)

It is the most widely method for Random Sample Consensus to estimate the fundamental matrix in the field of computer vision.And meanwhile,the estimation of fundamental matrix uncertainty based on Random Sample Consensus was paid more attention to.As for this problem,the estimation fundamental matrix of Random Sample Consensus has been studied here.And based on this,error rate of fundamental matrix and the standard deviation of epipolar mean distance have been chosen as the evaluation index of fundamental matrix uncertainty.And then,the methodology can be built to achieve the estimation of fundamental matrix uncertainty based on Random Sample Consensus.

Random Sample Consensus;fundamental matrix;error rate;mean distance of epipolar;standard deviation

2014-03-05；

2014-07-15

国家科技支撑计划项目(2012BAH35B02)；江苏省普通高校研究生科研创新计划项目(KYZZ_0213)

卞玉霞(1987-)，女，博士研究生,主要研究方向为视频三维建模及其质量评价。E-mail:byx310@163.com

10.3969/j.issn.1672-0504.2015.01.008

TP391.41

A

1672-0504(2015)01-0037-04