基于模糊神经网络的高寒路基纵向裂缝危险度综合评价

叶 敏，王铁权

(长安大学 公路养护装备国家工程实验室，陕西 西安 710064)



基于模糊神经网络的高寒路基纵向裂缝危险度综合评价

叶 敏，王铁权

(长安大学 公路养护装备国家工程实验室，陕西 西安 710064)

以高寒地区自然环境因素、设计因素、冻土因素三类致灾因子指标作为输入变量，根据模糊推理规则构建路基纵向裂缝评价的非线性映射关系，通过对输入知识的预处理和输出知识的后处理，将模糊逻辑推理融入神经网络的非线性计算中，建立了综合评价模型。以青藏公路典型路段K3+020段为例，基于11类致灾因子评价该路段纵向裂缝的危险度为2级。结果表明：高寒路基纵向裂缝危险度模糊神经网络综合评价模型可用于评价纵向裂缝的发育程度，经济性好、实用性强。

道路工程；路基工程；纵向裂缝；致灾因子；模糊神经网络

0 引 言

根据《国家公路网规划(2013年—2030年)》的长期规划，到2030年末，国家公路网新增高速公路约3.3万km，高寒地区占其中的80%～90%；国网普通公路新增11万km，高寒地区占其中的60%～70%。我国的公路建设重心已由中东部沿海转移到高寒地区，因高寒气候条件海拔高、低温时间长、温差大，高寒路基常出现早期开裂等病害[1]。高速公路作为国民经济的命脉，过早破损影响了道路服务能力，缩短了使用年限，阻碍了交通运输综合效益的发挥。公路养护和维修任务迫在眉睫，而裂缝发育程度评价结果会直接影响养护决策和资金投入，因此，建立客观实用的高寒路基纵向裂缝危险度评价模型十分重要[2-3]。目前道路病害综合评价方法和模型主要有回归分析法、系统分析评价法和灰色理论模型等[4-6]。朱东鹏等[4]利用回归分析方法提出了冻土路基纵向裂缝评价标准分为轻度、中度和重度；任贵波[5]利用可拓学物元理论建立模型，通过系统分析评价法分别对各纵缝破损等级和抽样路段纵缝总体破损状况进行评价；党奇志[6]采用灰色理论对旧沥青混凝土路面的路用性能进行了评价。但是，现有研究结果表明：回归分析模型不足以准确表征裂缝实测指标与专家评价结果之间的复杂联系，系统分析法中人为因素影响太大，灰色理论法模型依赖于评价指标的经验范围。已有的评价方法摆脱不了评价过程中的随机性以及评价专家主观上的不确定性和认识上的模糊性；另外，不能利用已有的比较成功的裂缝发育程度评价案例信息，专家的评价经验和知识得不到积累。高寒地区路基纵向裂缝危险度评价尚处于探索阶段[7]。笔者综合模糊逻辑与神经网络的优点，基于纵向裂缝发育的致灾因子，建立高寒路基纵向裂缝模糊神经网络综合评价模型来分析纵向裂缝发育的危险程度，并以青藏公路典型路段K3+020段为例分析其危险度。

1 路基纵向裂缝致灾因子分析

青藏公路全长1 937 km，其中550 km穿越自然环境恶劣、地质条件复杂的高原多年冻土地区，全线平均海拔在4 000 m以上，如图1(a)。海拔高、温度低、太阳辐射强、自然条件恶劣等致使路基路面病害相对突出，其中路基纵向裂缝与不均匀变形是最为典型的路基病害。纵向裂缝根据裂缝宽度和深度等可分为轻度、中度和重度等不同等级，如图1(b)和图1(c)。根据资料收集，归纳出诱发青藏公路路基纵向裂缝的致灾因子大致可划为3大类：自然环境因素、冻土因素和设计因素[8]。

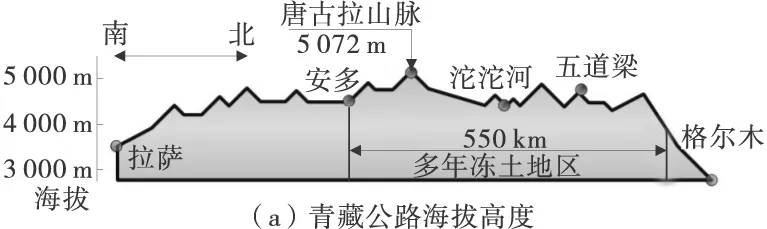
图1 青藏公路海拔及裂缝病害

高寒路基纵向裂缝评价体系如图2，主要评价指标包括自然环境因素、冻土因素和设计因素3大类，具体细分为地温、降水、太阳辐射等11个致灾因子[9-14]。

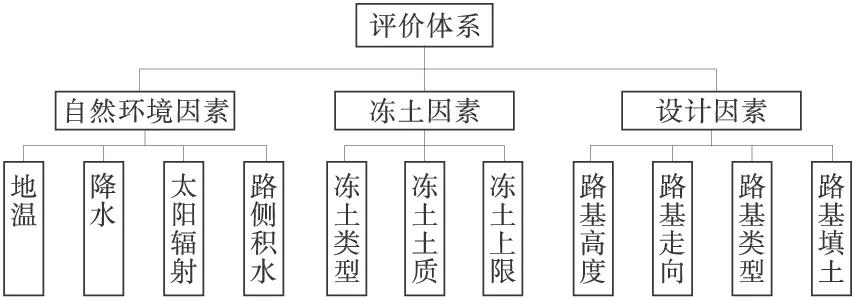
图2 纵向裂缝的评价体系

2 高寒路基纵向裂缝危险度分析

2.1 建立因素集及评价体系

因素集U是指以影响纵向裂缝发育的各致灾因子为元素所组成的集合，即：

U={U1,U2,…,Ui}；Ui={Ui1,Ui2,Ui3,…,Uin}

(1)

式中：Ui指因素集U中某类致灾因子。

2.2 确定致灾因子权重

为了反映致灾因子对纵向裂缝的影响程度，对各致灾因子赋予一定的权重，组成权向量。参照层次分析法中的标度，对评价体系中同一层各因子两两比较，得到判断矩阵。对判断矩阵做一致性检验，计算该矩阵的最大特征值，结合平均随机一致性指标，根据式(2)计算随机一致性比率，当时一致性检验通过，否则重新确定判断矩阵：

(2)

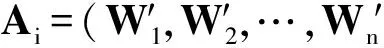
(3)

依次对评价体系各层采用层次分析法，得到各层的权向量Ai，然后得到致灾因子最终权向量A。

2.3 建立评价集

对路基纵向裂缝评价时将可能得出的评价结果组成评价集，即：

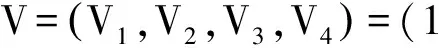
(4)

评价集中各评价结果参照等级划分表1。

表1 危险度等级划分

(续表1)

危险度指数等级说明3级0．2～0．4路基出现少数裂缝，裂缝分布稀疏，较发育，有危害路基稳定的发展趋势4级0～0．2路基无裂缝，或者裂缝数量很少且不发育，对路基基本无影响

2.4 单因素模糊评价

基于前面影响纵向裂缝形成的因素，以致灾因子单独对路基纵缝危险度进行评价如表2，确定其对评价集中各元素的权重，得到单因素评价向量，将所有单因素评价向量按行组成评判矩阵。

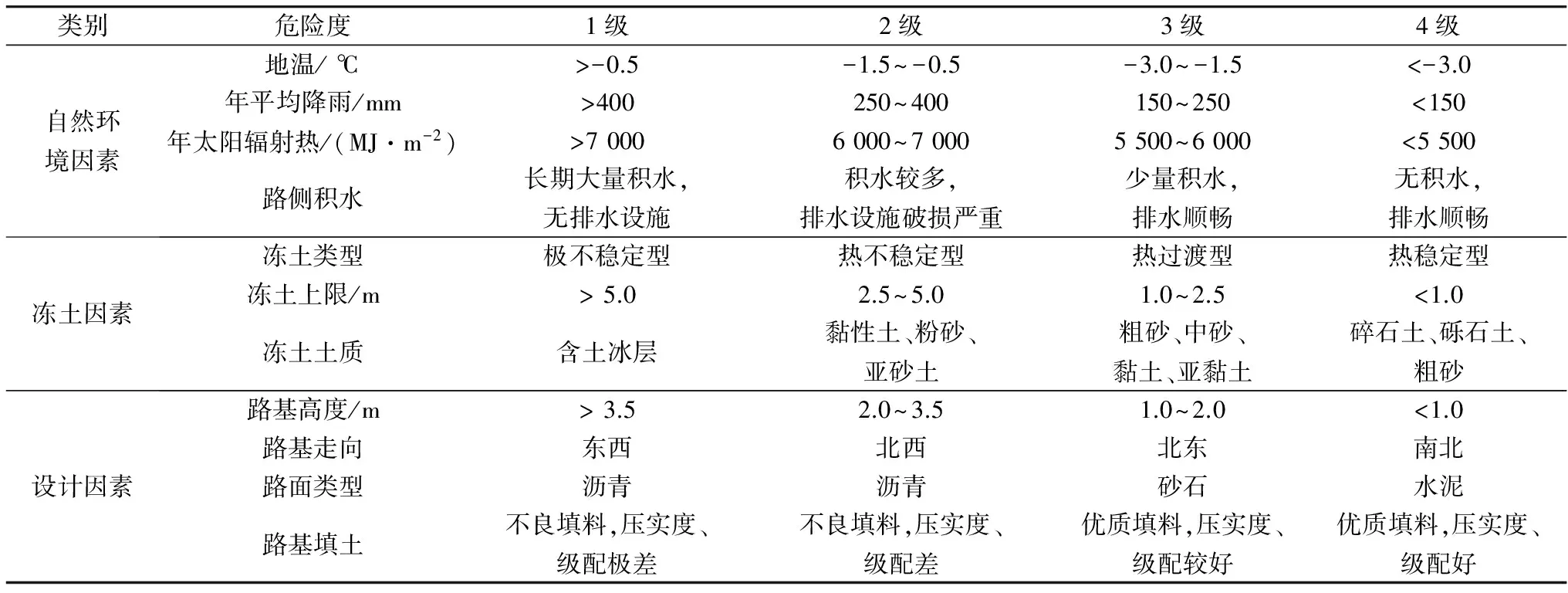
表2 单因素评价标准

2.5 模糊综合评价

通过上述评判矩阵P、权向量A，结合列向量H可得模糊综合评价式如式(5)：

B=A·P=(bij)

(5)

M=B·H

(6)

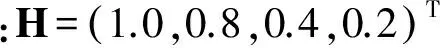
将B归一化后带入式(6)，将所得值M参照表1中的危险度指数，确定纵向裂缝的危险度等级。

3 路段纵缝危险度评价分析

以青藏公路K3+020段为例，采用模糊神经网络综合评价法分析该段路基纵向裂缝的危险度[15]。该路段位于五道梁地区，海拔4 600 m以上，高寒低氧，气候恶劣。该地区年平均气温为-5.6 ℃，气温变化图型为单峰型，如图3(a)。年平均降雨量随季节差异性很大，1—5月降雨量极少，而6—9月则是降雨集中期，如图3(b)，年均降水量为40 mm左右，这种季节性降雨导致道路两侧出现季节性积水。该路段太阳辐射量大，5—7月太阳总辐射量最大，最大辐射量为24 MJ/(m2·d)。该路段多年冻土连续，有局部融区，多年冻土厚度达40～60 m，季节融化深度最深达1.5～2.8 m左右。实际勘察得知，该路段天然地表10 m以下就有纯厚冰层，土路肩3 m以下出现厚达1 m的纯冰层，冻土现象表现出冰锥、冻胀丘等，冻土稳定性较差。该路段路面由沥青面层、水泥稳定基层组成，路基高3 m，顶面宽10 m，填土为碎石土。

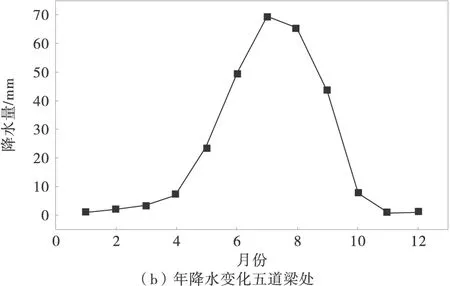
图3 青藏公路典型路段气候条件

神经网络训练过程中通过不断调整权重和偏置节点间的关系，以获得所期望的输入输出。在隐层和输出层中的每个神经元都有其各自的权重值和传递函数。一般来说，一个神经网络的运行能力取决于它的体系结构和其参数的设置。寻找最佳神经网络的过程中一个最主要的问题就是，确保隐层最优化和用试错法确定其神经元。根据各层所使用的函数的类型，确定各输入值的权重和人工神经网络的算法。在BP神经网络结构中，在输入输出的基础上，将训练的实例输入网络。将网络的输出值与相应的实测值进行比较。其次，在网络输出值与实际值的比较中发现错误。然后，通过反向传播，由输出修改网络输入的权重。这是一种减少网络错误的方法。当实际值与对应的网络收敛完成后，训练过程结束。总的可用数据是12个，如表3，其中80%用于训练，10%用于神经网络模拟能力的评价，10%用于评估训练效果并防止过度训练或使训练在模拟效果最佳时停止。用均方差(MSE)来确定最佳神经网络，其中误差最小的为最佳神经网络。网络训练过程如图4。在图4中，水平轴表示的是训练周期(阶段)，垂直轴表示的是均方差(MSE)。训练应在第13个周期停止，这是训练效果的最佳点。验证数据的相关系数R=0.982 77，测试数据的相关系数为0.998 18。

图4 神经网络的训练过程

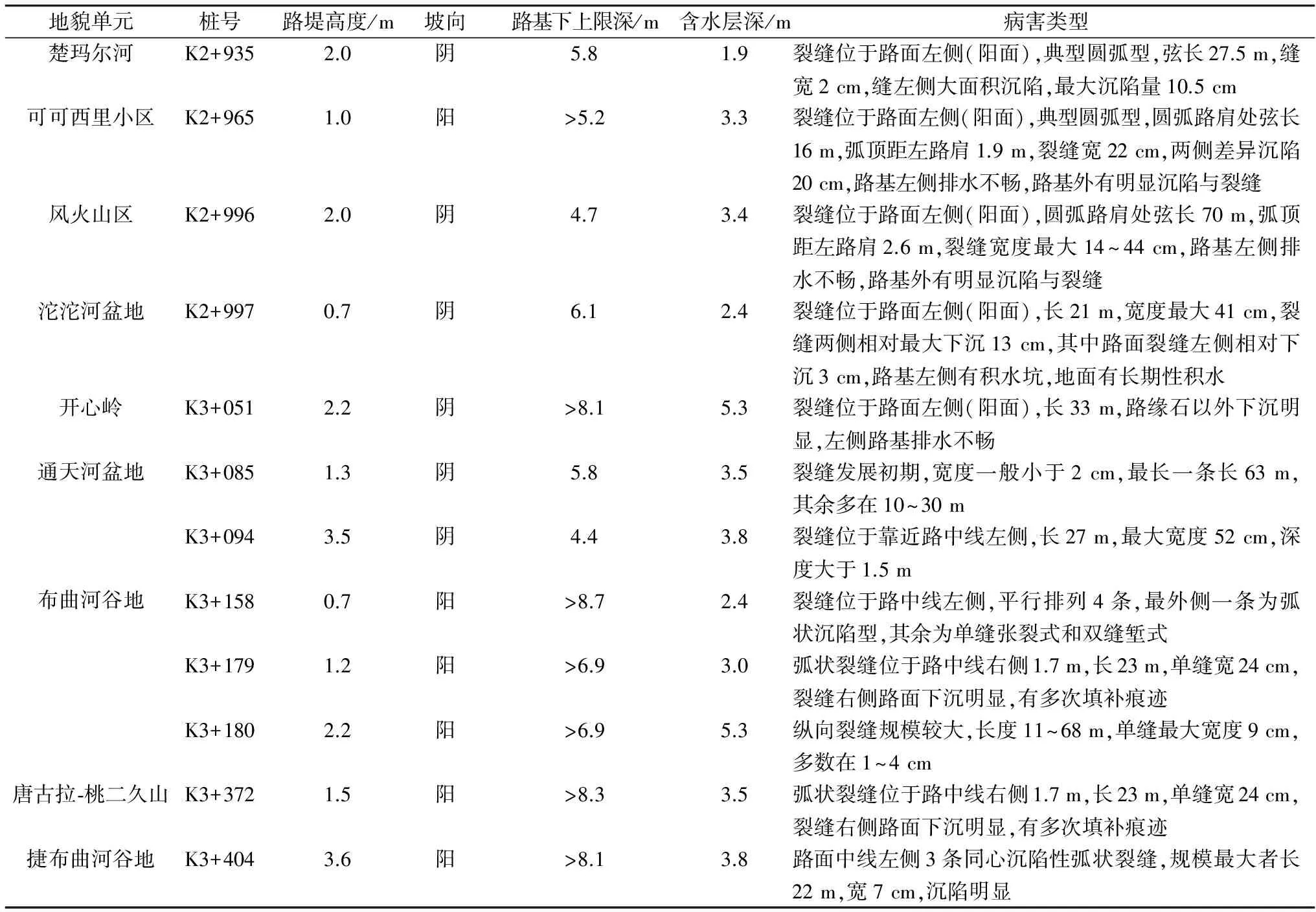
表3 纵向裂缝现场资料

根据K3+020路段所处的自然环境和路基参数，经过神经网络训练确定图2评价体系中自然环境因素、冻土因素、工程因素的权重a1，a2，a3，有：

构造自然环境因素下各致灾因子的判断矩阵N1：

(7)

该矩阵λmax=4.031 0，4阶矩阵取RI=0.9，根据式(2)有：

CR=0.011<0.10

(8)

A=(0.048 1，0.126 7，0.089 6，0.235 6，0.109 4，0.021 7，0.068 9，0.176 7，0.071 5，0.036 9，0.014 9)

(9)

根据表1、表2，确定各致灾因子对评价集元素的权重，将所有单因素评价向量组成评判矩阵P如式(10)：

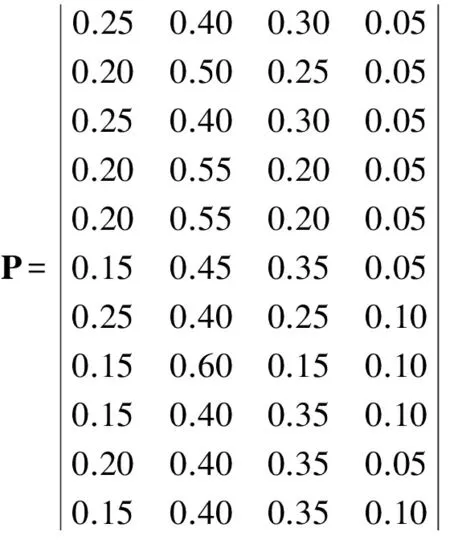
(10)

将评判矩阵P和权向量A带入式(5)得：

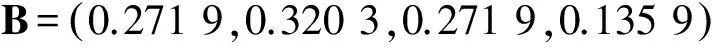
4 结 论

1)引入模糊理论和神经网络技术，提出基于模糊神经网络的纵向裂缝危险度评价方法，通过网络来完成评价的推理过程，克服了传统评价方法评价结果较为粗糙、评价过程较为依赖专家经验、评价速度慢等缺点。

2)将诱发青藏公路路基纵向裂缝形成的致灾因子划分为自然环境因素、冻土因素、设计因素三大类。

3)以青藏公路K3+020路段为例进行评价，评价结果为该路段纵向裂缝危险度为2级，与专家现场评判结果一致，得出所建模型可客观、快速和精确地分析多年冻土地区路基纵向裂缝危险度的结论。

[1] 杨锦凤.水热变化对青藏公路路基纵向裂缝的影响研究[D].西安:长安大学,2013. Yang Jinfeng.Study on the Changes of Moisture and Heat Impact on the Longitudinal Cracks of Subgrade in Qinghai-Tibet Highway [D].Xi’an:Chang’an University,2013.

[2] Eker R,Aydin A.Assessment of forest road conditions in terms of landslide susceptibility:a case study in Yiglca lca Forest Directorate (Turkey) [J].Turkish Journal of Agriculture and Forestry,2014,38(2):281-290.

[3] Zou Jian,Roque R,Chun S,et al.Long-term field evaluation and analysis of top-down cracking for Superpave projects [J].Road Materials and Pavement Design,2013,14(4):831-846.

[4] 朱东鹏,贾志裕,章金钊.青藏公路路基纵向裂缝发育规律与整治措施研究[J].公路,2009(9):328-329. Zhu Dongpeng,Jia Zhiyu,Zhang Jinzhao.Study on formation regularity and rectification measures of the Qinghai-Tibet highway longitudinal cracks [J].Highway,2009(9):328-329.

[5] 任贵波.季冻区沥青路面纵向裂缝破损状况评价与成因分析[D].哈尔滨:东北林业大学,2011. Ren Guibo.Evaluation on the Damage Condition and Analysis of the Formation Cause of Longitudinal Cracks on Bituminous Pavement in Seasonal Frozen Region [D].Harbin:Northeast Forestry University,2011.

[6] 党奇志．基于灰色理论的旧沥青混凝土路面使用性能综合评价方法[J].公路,2011(11) :207-209. Dang Qizhi.Based on the theory of gray system of old asphalt concrete pavement performance evaluation method [J].Highway,2011(11) :207-209.

[7] 刘艳,康海贵,孙敏．基于遗传算法的模糊优选神经网络路面性能评价模型[J]．大连理工大学学报,2010,50(1):117-122. Liu Yan,Kang Haigui,Sun Min.Genetic algorithm-based fuzzy optimization neural network model for pavement performance evaluation [J].Journal of Dalian University of Technology,2010,50(1):117-122.

[8] 裴建中,窦明建,胡长顺,等.多年冻土地区路基纵向裂缝影响因素[J].长安大学学报:自然科学版,2007,27(6):16-18. Pei Jianzhong,Dou Mingjian,Hu Changshun,et al.Influence factors of embankment longitudinal cracks in permafrost regions [J].Journal of Chang’an University:Natural Science Edition,2007,27(6):16-18.

[9] 代寒松,盛煜,陈继.青藏公路路基纵向裂缝病害及其发生规律[J].公路,2006(1):86-87. Dai Hansong,Sheng Yu,Chen Ji.Longitudinal roadbed cracks in Qinghai-Tibet highway and its forming regularity [J].Highway,2006(1):86-87.

[10] 毛雪松,凌思德,张正波,等.路侧积水对青藏公路路基强度的影响分析[J].武汉理工大学学报:交通科学与工程版,2013,37(3):457-458. Mao Xuesong,Ling Side,Zhang Zhengbo,et al.Analysis the influence of hydrops along the subgrade to Qinghai-Tibet highway subgrade strength [J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2013,37(3):457-458.

[11] 赵平,董淑海,许兆义,等.加筋土抑制多年冻土区路基工程裂缝的效果评价[J].北京交通大学学报,2011,35(4):14-16. Zhao Ping,Dong Shuhai,Xu Zhaoyi,et al.Effectiveness evaluation for reinforced geogrids to inhibiting embankment cracks in permafrost area [J].Journal of Beijing Jiaotong University,2011,35(4):14-16.

[12] 李金明,周育名,原喜忠.气温升高对多年冻土地区路基稳定性影响[J].重庆交通大学学报:自然科学版,2011,30(2):264-265. Li Jinming,Zhou Yuming,Yuan Xizhong.Impact of climate warming on subgrade stabilization in permafrost areas [J].Journal of Chongqing Jiaotong University:Natural Science,2011,30(2):264-265.

[13] 温智,盛煜,马巍,等.国道214线多年冻土地区公路路基典型纵向裂缝监测和模拟研究[C]∥第三届全国岩土与工程学术大会.成都:四川科学技术出版社,2009:50-52. Wen Zhi,Sheng Yu,Ma Wei,et al.Typical subgrade longitudinal cracks monitoring and simulation study of state road 214 in permafrost regions [C]∥The 3rdAcademic Conference of National Geotechnical and Engineering.Chengdu:Sichuan Science & Technology Press,2009:50-52.

[14] 窦明健,胡长顺,何子文,等.青藏公路多年冻土段路基病害分布规律[J].冰川冻土,2002,24(6):780-783. Dou Mingjian,Hu Changshun,He Ziwen,et al.Distributing regularities of subgrade diseases in permafrost section of the Qinghai-Tibet highway [J].Journal of Glaciology and Geocryology,2002,24(6):780-783.

[15] 丑亚玲,蒋先刚,朱彦鹏.高温多年冻土区路基纵向裂缝发育的热-力耦合分析[J].兰州理工大学学报,2014,40(1):124-128. Chou Yaling,Jiang Xiangang,Zhu Yanpeng.Thermo-mechanical coupled analysis on the embankment longitudinal cracks in warm permafrost regions [J].Journal of Lanzhou University of Technology,2014,40(1):124-128.

Comprehensive Risk Evaluation on the Longitudinal Cracks of Permafrost Subgrade Based on Fuzzy Neural Network

Ye Min, Wang Tiequan

(National Engineering Laboratory for Highway Maintenance Equipment, Chang’an University, Xi’an 710064, Shaanxi, China)

The natural environment factor, the design factor and the frost soil factor for the permafrost subgrade crack damage evaluation were selected as the input vector. According to the fuzzy rule, the nonlinear mapping relation of the longitudinal crack evaluation of subgrade was established. Through the combination of input pretreatment and output post treatment, the fuzzy rule was embedded into the nonlinear calculation of the neural network. It evaluated the longitudinal cracks risk degree in the section of K3+020 of Qinghai-Tibet Highway and the disk degree was defined as second grade based on 11 kinds of damage factors. The results show that the model can quickly, accurately and objectively evaluate the subgrade longitudinal cracks risk degree in permafrost regions.

road engineering; subgrade; longitudinal cracks; hazard factor; fuzzy neural network

10.3969/j.issn.1674-0696.2015.04.12

2014-09-01；

2014-11-20

交通运输部科技项目(201231879210)

叶 敏(1978—)，男，吉林磐石人，副教授，博士，主要从事模糊神经网络等智能评价方法的研究。E-mail：mingye@chd.edu.cn。

TU433

A

1674-0696(2015)04-068-05