区间犹豫模糊ELECTRE多属性决策方法及应用

于 倩， 侯福均， 翟玉冰， 杜玉琴

(北京理工大学 管理与经济学院， 北京 100081)



区间犹豫模糊ELECTRE多属性决策方法及应用

于 倩， 侯福均， 翟玉冰， 杜玉琴

(北京理工大学 管理与经济学院， 北京 100081)

近年来，多属性决策问题一直是广大学者研究的重点，然而基于ELECTRE方法的区间犹豫模糊多属性决策问题的研究并不多见。因此，结合区间犹豫模糊集的信息表达优势和ELECTRE方法的思想，提出了一种区间犹豫模糊ELECTRE(IVHF ELECTRE)多属性决策新方法。首先构造了区间犹豫模糊决策矩阵，引入得分函数和可能度的概念，构造属性优势集和属性劣势集。然后通过设定阈值得到综合优先判定矩阵，从而得到各方案间的优先顺序。为了进一步得到各方案的整体排序，引入TOPSIS方法，通过计算各方案与正负理想点的相对距离来构造综合优先矩阵，从而得到各方案的总体排序。最后通过具体实例验证了该方法的可行性和合理性。

IVHF ELECTRE方法；多属性决策(MADM)；区间犹豫模糊集(IVHFS);TOPSIS

0 引言

多属性决策问题广泛地存在于各个领域和人们的日常生活中，一直以来成为人们研究的重点。ELECTRE方法作为多属性决策中的一种代表性方法，由于其实用性强，已在各个领域获得了广泛而成功的应用[1,2]。1965年Zadeh[3]提出了模糊集理论。随后，许多学者开始用模糊理论扩展经典的多属性决策问题。

但随着决策复杂性和评价信息不确定性的增加，模糊集已经不能满足这些需求。于是2010年，Torra[4]提出了犹豫模糊集的概念，它是传统模糊集理论的一个重要扩展形式。它允许某个元素对集合的隶属程度以[0,1]上几个可能值的集合的形式给出，从而在一定程度上避免了决策中的信息损失。考虑到客观环境的复杂性、决策者的知识结构和专业水平以及时间等诸多因素影响，决策者在给定评价信息时难以用精确的数值来表示评价信息，因此将区间数推广到犹豫模糊集中。2013年，Xu[5]提出了区间犹豫模糊集的概念。自此有关区间犹豫模糊集在多属性决策(MADM)领域的应用就成了众多学者研究的主题。

ELECTRE(Elimination Et Choice Translating Reality)方法首次由Benayoun，Roy与Sussman[6]于20世纪60年代提出。随后很多学者将其进行发展，形成了具有不同形式的ELECTRE方法族，包括ELECTREⅠ[7]，ELECTREⅡ[8]， ELECTRE TRI[9]，ELECTRE Ⅳ[10]。事实上，很多学者已将ELECTRE方法应用于不同的模糊环境中，如区间数[11]，梯形模糊数[12]，三角模糊数[13]，直觉模糊数[14]等。但迄今为止，ELECTRE方法在区间犹豫模糊多属性决策中的应用研究还不多见。因此对经典的ELECTRE方法进行了改进，将其拓展到区间犹豫模糊集环境下，其中不确定信息以区间犹豫模糊元的形式给出，以此解决区间犹豫模糊多属性决策问题。

1 相关概念

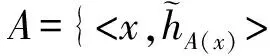
定义2[5]区间犹豫模糊元的运算法则

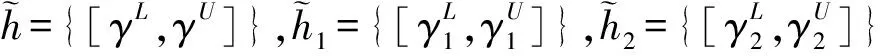
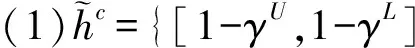
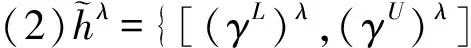
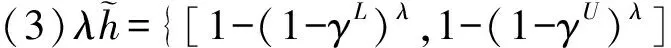
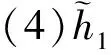
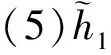
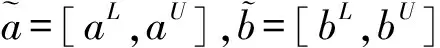
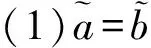
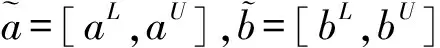
(1)

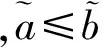
(2)

从以上定义可得

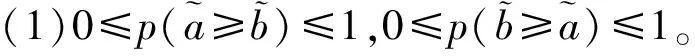
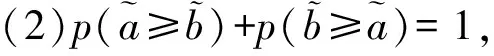
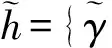
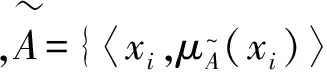
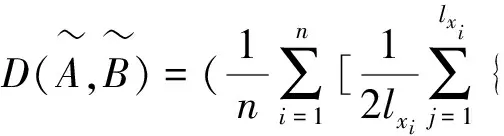
(3)

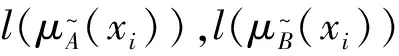
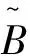
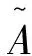
2 区间犹豫模糊ELECTRE方法

研究在区间犹豫模糊集环境下，引入得分函数和可能度的概念，建立各区间犹豫模糊元得分函数的可能度矩阵，将区间犹豫模糊元的排序问题转换为优劣关系与之等价的一组精确值来实现。这样对于区间犹豫模糊多属性决策问题就可以通过得分函数的可能度矩阵的建立，再映射为一组优劣关系与原区间犹豫模糊元等价的实数形式，从而对各方案在各个属性上评价信息的优劣关系进行两两比较和排序，然后再应用区间犹豫模糊ELECTRE(IVHF ELECTRE)模型来解决区间犹豫模糊环境下的多属性决策问题。

2.1 区间犹豫模糊决策矩阵

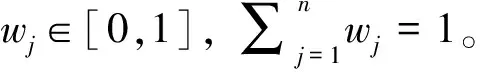
2.2 区间犹豫模糊级别高于关系的构造

级别高于关系是ELECTRE方法的核心思想，而IVHF ELECTRE方法是将ELECTRE方法拓展到区间犹豫模糊环境中，因此区间犹豫模糊ELECTRE方法的核心思想也是级别高于关系的构造。在传统的ELECTRE方法中，不同的ELECTRE方法具有不同的级别高于关系，所有的这些级别高于关系都是在实数信息表示的基础上提出来的。而这里所介绍的方法中的级别优先关系是基于区间犹豫模糊元表示形式的。

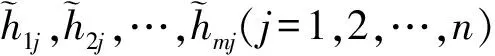
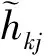
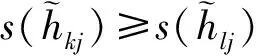
(4)

k,l=1,2,…,m,j=1,2,…,n

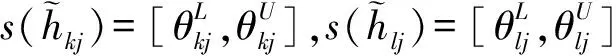
(2)得到可能度矩阵Pj。

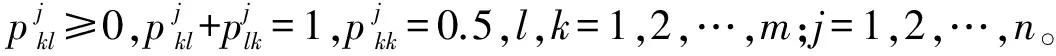
(3)对矩阵pj的每一行进行求和，得到

对于方案Ak和Al(k,l=1,2,…,m,k≠l)，决策属性集被划分为两个不同的子集，即属性优势集和属性劣势集。

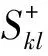
属性优势集可用下列式来表示：

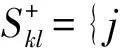
(5)

属性劣势集为优势集的补集，意义正好和优势集相反，即Al方案的各目标属性优于方案Ak对应的目标属性的属性标号集合。

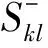
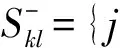
(6)

2.3IVHFELECTRE方法

IVHF ELECTRE方法是区间犹豫模糊信息和ELECTRE方法的结合。它不同于传统的决策方法，它是基于属性间的优先序，利用级别优先关系来对方案进行优选，排序和分类。

(7)

优势指标反映了Ak相对于Al的重要性程度的大小，ekl越大意味着对所有的优势指标而言，Ak对Al越具有优势，且0≤ekl≤1。

当计算出所有方案对的优势指数ekl(k≠l,j=1,2,…,n)时，就构成了如下的优势矩阵E=(ekl)m×n。

对于属性劣势集，我们利用下式来计算Ak劣于Al的程度：

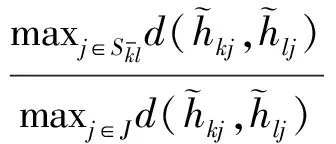
(8)

其中

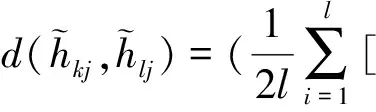
fkl表示分子为属性劣势集中的标号所对应的两个方案之间的距离中的最大值，分母为所有目标属性的两个方案之间的距离中的最大值，两者相除则表示Ak比Al的劣势程度。同样0≤fkl≤1。fkl值越小，则意味着对所有的劣势指标而言，Ak越优于Al。

当计算出所有的劣势指标fkl(k≠l)后，可得如下的劣势矩阵F=(fkl)m×n。

阀值可以人为给定，也可用平均优势指标表示，即

(9)

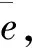
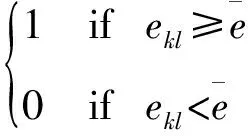
(10)

当这个矩阵U的元素为1 时，意味着具有优势机会(或可能)。

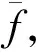
(11)

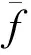
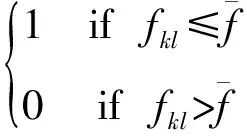
(12)

U和V中的对应元素相乘的结果，就构成了所谓综合优势判定矩阵Z=(zkl)m×n中的元素zkl，即

zkl=μkl·vkl

(13)

根据综合优势判定矩阵Z，如果zkl=1，则Ak整体优于Al，但仍有其他方案优于Ak的可能。因此对于Ak而言只有下式满足，它才不会被剔除。

(14)

上式的实际应用是较困难的，然而我们可以在Z上直观地进行分析剔除方案，也即若任何列上只要有一个元素为1，则该列对应的方案从最优方案中剔除。

根据上述方法，我们仅能剔除不理想的方案，也仅能得到各方案的部分优先顺序。然而，我们无法得到各方案的完全排序。因此为了得到方案间的整体排序，我们引入了TOPSIS方法。它使得具有优势的方案应该具备距离正理想点最近而距离负理想点最远的特性。从而定义了基于TOPSIS方法的优势比较判定矩阵X=(xkl)m×n，其中

xkl=e*-ekl

(15)

e*表示优势矩阵E=(ekl)m×n中最大元素值，记为正理想点。

同样基于TOPSIS方法的劣势比较判定矩阵Y=(ykl)m×n的定义如下：

ykl=f*-fkl

(16)

f*表示劣势矩阵F=(fkl)m×n中最大元素值，记为负理想点。

计算各方案到正负理想点的相对贴近度，得到综合优先矩阵R=(rkl)m×n，其中

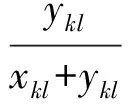
(17)

rkl表示方案Ak相对于Al到正负理想点的相对贴近度。rkl值越高，表明Ak相对于Al来说，越接近于正理想点，越远离于负理想点。

然后计算各方案的综合评价值，

(18)

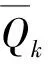
(19)

2.4 决策过程

根据上述分析，IVHF ELECTRE方法的分析步骤如下：

步骤1 通过专家对各方案相对于各属性进行评价，确定区间犹豫模糊决策矩阵。

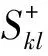
步骤3 根据式(7)，式(8)计算优势矩阵E=(ekl)m×n和劣势矩阵F=(fkl)m×n。

步骤4a) 由式(9)，式(11)计算优劣势指数阈值，并根据式(10)，式(12)来确定优势0-1布尔矩阵U=(μkl)m×n和劣势0-1布尔矩阵Y=(ykl)m×n。

步骤4b) 通过引入TOPSIS方法，根据式(15)，式(16)确定优势比较判断矩阵X=(xkl)m×n和劣势比较判断矩阵Y=(ykl)m×n。

步骤5a) 根据式(13)计算优劣势布尔矩阵的乘积，来确定综合优劣判定矩阵Z=(zklm×n)。

步骤5b) 根据式(17)计算各方案到正负理想点的相对贴近度，确定综合优先矩阵R=(rkl)m×n，并由式(18)确定各方案的综合评价值。

步骤6a) 由式(14)确定剔除较劣的方案，得到各方案的部分优先序。

步骤6b) 根据式(19)比较各方案综合评价值的大小，对各方案进行整体排序。

3 实例分析

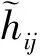
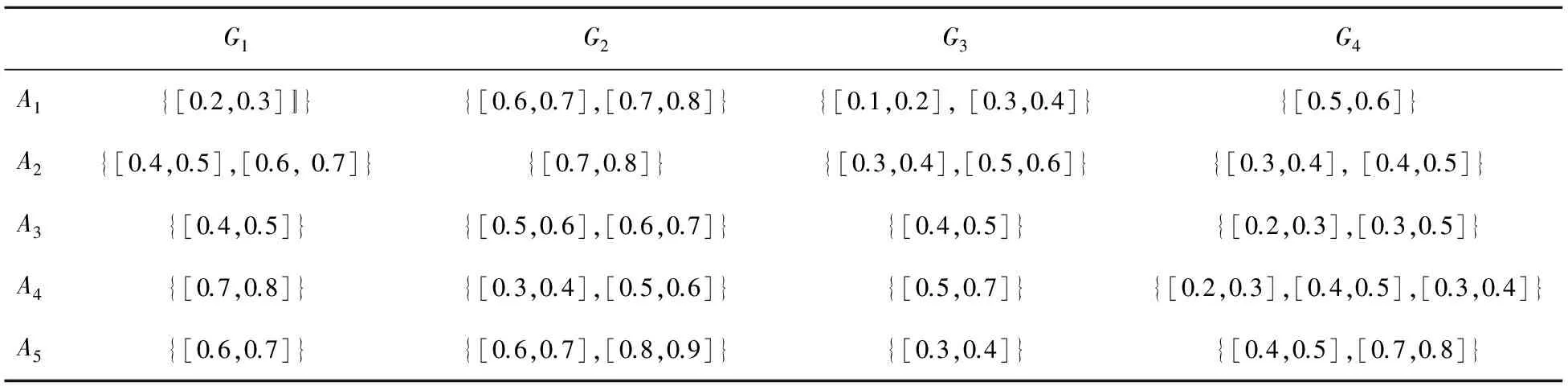
表1 区间犹豫模糊决策矩阵

步骤2 各方案在各属性上评价信息的得分计算如表2所示。通过比较各得分值，从而比较各方案在各个属性上的优劣程度。

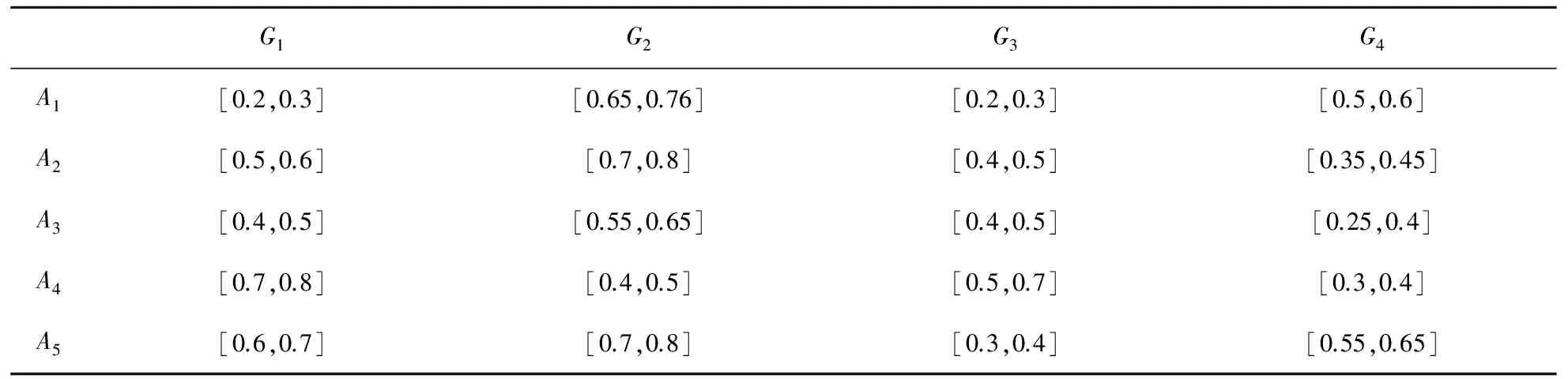
表2 区间犹豫模糊得分值

计算属性优势集得

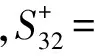
确定属性劣势集得

步骤3 根据式(7)计算优势矩阵

其中

其他元素值的计算方法同上。

根据式(8)计算劣势矩阵

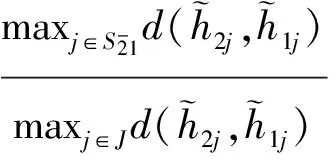
其他元素值的计算方法同上。

步骤4a 根据式(9)计算平均优势指数值

通过式(10)计算优势0-1布尔矩阵

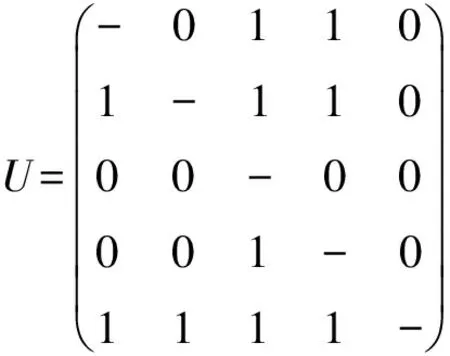
根据式(11)计算平均劣势指数值

通过式(12)计算劣势0-1布尔矩阵

步骤4b 引入TOPSIS方法，根据式(15)计算优势比较判断矩阵

根据式(16)计算劣势比较判断矩阵

步骤5a 根据式(13)计算综合优先矩阵Z

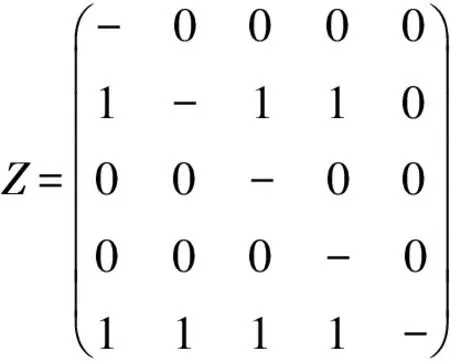
步骤5b根据式(17)计算各方案到正负理想点的相对贴近度，确定综合优先矩阵

根据式(18)计算各方案的综合评价值。

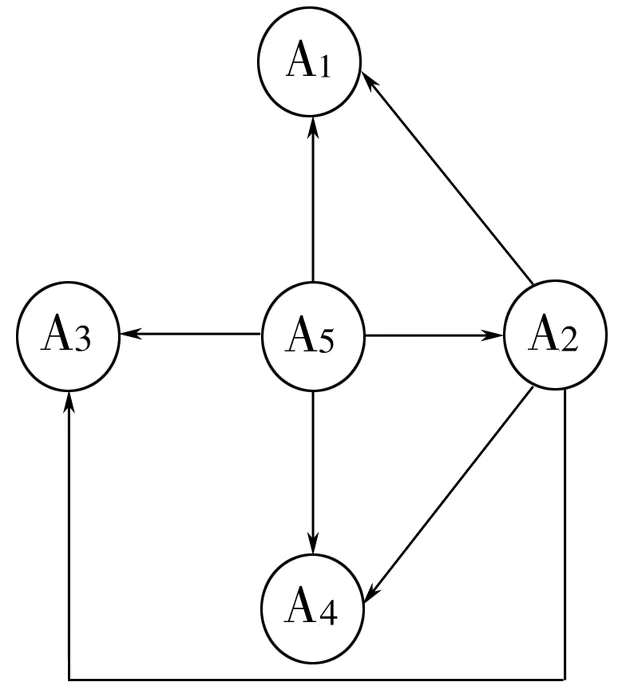
图1 方案间的优先关系图

步骤6a 根据式(14)，A5被选入最优方案。矩阵反映了方案的优先顺序，如图1所示：

A2>A1,A2>A3,A2>A4,A5>A1,A5>A2,A5>A3,A5>A4

从Z可以看出，我们仅能得到各方案间的部分优劣关系，而不能得到方案的整体排序。

步骤6b 根据式(19)比较各方案综合评价值的大小，最后得出各方案的整体排序为A5>A2>A4>A1～A3。因此最优方案仍是A5。

4 结束语

基于ELECTRE方法理论和区间犹豫模糊信息，提出了区间犹豫模糊ELECTRE(IVHF ELECTRE)方法来处理模糊多属性决策问题。通过引入可能度和得分函数的概念，对各个指标下一组区间犹豫模糊元两两比较，建立得分函数的可能度矩阵，将这组区间犹豫模糊元信息映射为与之优劣关系等价的精确值形式，对每个属性下的区间犹豫模糊元进行同样的操作进而完成对原始决策信息的改造，使之与现有的决策模型相吻合。该方法既是对基于区间犹豫模糊集的多属性决策模型的丰富，也是对经典ELECTRE方法在区间犹豫模糊环境下的一个扩展。它既充分利用了区间犹豫模糊信息，又保留了ELECTRE方法计算简洁的优势，易于决策者的掌握和使用。经实例验证，该方法具有一定的合理性和可行性。

[1] Brito A J, de Almeida A T, Mota C M M. A multi-criteria model for risk sorting of natural gas pipelines based on ELECTRE TRI integrating utility theory[J]. European Journal of Operational Research, 2010, 200(3): 812- 821.

[2] Petrovic M, Bojkovic N, Anic I, Stamenkovic M, Tarle S P. An ELECTRE-based decision aid tool for stepwise benchmarking: an application over EU Digital Agenda targets[J]. Decision Support System, 2014, 59: 230-241.

[3] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353.

[4] Torra V. Hesitant fuzzy sets[J]. International Journal of Intelligent Systems, 2010, 25(6): 529-539.

[5] Chen N, Xu Z S, Xia M M. Interval-valued hesitant preference relations and their applications to group decision making[J]. Knowledge-Based Systems, 2013, 37: 528-540.

[6] Benayoun R, Roy B, Sussmann B. ELECTRE: Une méthode pour guider le choix en présence de points de vue multiples SEMA(Metra International)[J]. Direction Scientifique, Notre de travail, 1966, 49.

[7] Almeida A T. Multicriteria modelling of repair contract based on utility and ELECTRE I method with dependability and service quality criteria[J]. Annual Operation Research, 2005, 138(1): 113-126.

[8] Duckstein L, Gershon M. Multicriterion analysis of a vegetation management problem using ELECTRE-II[J]. Applied Mathematical Modelling, 1983, 7(4): 254-261.

[9] Raju K S, Duckstein L, Arondel C. Multicriterion analysis for sustainable water resources planning: a case study in spain[J]. Water Resource Management, 2000, 14(6): 435- 456.

[10] Shanian A, Savadogo O. A non-compensatory compromised solution for material selection of bipolar plates for polymer electrolyte membrane fuel cell(PEMFC)using ELECTRE IV[J]. Electrochimica Acta, 2006, 51(25): 5307-5315.

[11] Vahdani B, Jabbari A H K, Roshanaei V, Zandieh M. Extension of the ELECTRE method for decision-making problems with interval weights and data[J]. International Journal of Advanced Manufacturing Technology, 2010, 50(5- 8): 793- 800.

[12] Hatami-Marbini A, Tavana M. An extension of the Electre I method for group decision-making under a fuzzy environment[J]. Omega, 2011, 39 (4): 373-386.

[14] Vahdani B, Mousavi S M, Tavakkoli-Moghaddam R, Hashemi H. A new design of the elimination and choice translating reality method for multi-criteria group decision-making in an intuitionistic fuzzy environment[J]. Applied Mathematical Modelling, 2013, 37(4): 1781-1799.

[15] Xu Z S, Da Q L. The uncertain OWA operator[J]. International Journal of Intelligent Systems, 2002, 17(6): 569-575.

[16] Wei G W, Lin R, Wang H. J. Distance and similarity measures for hesitant interval-valued fuzzy sets[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(1): 19-36.

ELECTRE-Based Measure for Multi-Attribute Decision Making Using Interval-Valued Hesitant Fuzzy Set

YU Qian, HOU Fu-jun, ZHAI Yu-bing, DU Yu-qin

(SchoolofManagementandEconomics,BeijingInstituteofTechnology,Beijing100081,China)

For the past decades, the multi-attribute decision making problem has always been the focus of many scholars. However, there is a still blank in using the ELECTRE(Elimination Et Choice Translating Reality)method to solve multi-attribute decision making(MADM)problems with interval-valued hesitant fuzzy information. By combining the expression advantage of interval-valued hesitant fuzzy sets and the idea of the ELECTRE method, an interval-valued hesitant fuzzy ELECTRE(IVHF ELECTRE)method is proposed. Firstly, the interval-valued hesitant fuzzy decision matrix is constructed, and the concordance set and discordance set are defined by introducing the concept of score function and possibility. Then comprehensive judgment matrix is calculated by setting the threshold value to obtain the preference ranking of the alternatives. In order to further get overall sort of the alternatives, the TOPSIS method is introduced. And the comprehensive preference matrix is constructed by calculating the distance between each alternative and the ideal point to obtain the complete ranking of the alternatives. Finally, an illustrative example is given to verify the developed approach and to demonstrate its practicality and effectiveness.

IVHF ELECTRE method; multi-attribute decision making(MADM); interval-valued hesitant fuzzy set(IVHFS); TOPSIS

2014-10-21

国家自然科学基金资助项目(71571019)

于倩(1984-)，女，博士研究生，研究方向：多属性决策，最优化分析；侯福均(1967-)，男，副教授，博士生导师，研究方向：决策理论与方法，运筹与优化，不确定理论及应用。

C934

A

1007-3221(2015)06- 0016- 09

10.12005/orms.2015.0191