基于资源随机中断的反应性多模式项目调度优化
2015-06-07李佳媛何正文
李佳媛, 何正文
(西安交通大学 管理学院,陕西 西安 710049)
基于资源随机中断的反应性多模式项目调度优化
李佳媛, 何正文
(西安交通大学 管理学院,陕西 西安 710049)
资源中断是项目实施过程中一种常见现象,它会导致项目进度计划的变更并引起额外的成本。本文研究资源随机中断下的项目调度问题,目标是对基准进度计划进行合理的调整,以最小化由此所造成的额外成本。作者首先对研究问题进行界定,随后构建问题的优化模型。针对模型的NP-hard属性,设计禁忌搜索启发式算法。最后以基准列表算法和随机生成算法为参照,在随机生成的标准算例集合上对算法进行测试,得到如下结论:在可接受的计算时间范围内,禁忌搜索获得的满意解质量明显高于其他两种启发式算法;算法的平均计算时间随着项目活动数的增加而增加,随着网络复杂度、资源强度或资源中断次数的增加而减小;满意解的平均目标函数值,随着项目活动数或网络复杂度的增加而增加,随着资源中断次数的增加而减小,与资源强度无明显关系。
反应性项目调度;优化模型;禁忌搜索;资源随机中断
0 引言
由于内外部诸多不可预见因素的干扰,现实中的绝大多数项目在执行过程中都不可避免地会发生变更[1]。项目的变更无疑会引起进度计划的调整、资源配置的改变,进而影响项目的平稳实施并由此产生额外成本。
在项目执行过程中,如何基于实际情况对基准进度计划进行调整,在理论上被称为反应性项目调度问题(Reactive Project Scheduling Problem)[2]。关于该问题,目前已有学者开始进行研究:Vonder等[3]对已有的多种前摄性调度和反应性调度算法进行了对比测试,找到了计算效果较好的算法组合。Vonder等[4]还提出了多种最小化实际与计划进度偏差的反应性调度启发式算法。Deblaere等[5]设计了针对活动工期不确定的反应性调度启发式算法,并推导出了相应的进度计划稳定性下界。Lambrechts等[6]设计了单模式下针对资源中断的多种计划生成策略与反应性调度策略并进行了测试。Deblaere等[7]开发了将活动开始时间延后与执行模式改变同步进行的反应性调度精确算法与启发式算法,并对精确算法、启发式算法及多种算法结合的情况进行了测试分析。任世科等[8]研究了突发事件应急救援的动态调度优化问题,构建了相应的动态调度优化模型,并设计了禁忌搜索启发式算法。然而,必须指出的是,当前对该问题的研究尚处于起步阶段,亟待进一步的深入和扩展。
值得注意的是,在造成项目变更的各种因素中,资源问题是最为突出的因素之一。其中,在项目实施过程中一个经常遇到的问题,便是项目资源的随机中断[9][10]。资源随机中断是指由于各种干扰因素的作用,导致项目资源在某一随机时段上的不可使用。显然,当资源随机中断发生时,项目管理者将不得不对基准进度计划,包括各活动的执行模式和开始时间进行调整。本文正是基于上述理论和现实背景,研究资源随机中断下的反应性项目调度问题。即研究如何基于资源中断对基准进度计划进行调整,以使得由此产生的额外总成本最小化。
在论文的后续部分,作者首先对所研究问题进行界定。随后,构建基于资源随机中断的反应性多模式项目调度优化模型。针对问题的NP-hard属性,设计禁忌搜索启发式算法。在随机生成的标准算例集合上对算法进行测试分析。最后,总结全文并给出研究结论。
1 问题界定
本文采用基于活动(Activity-based)的研究方法,将项目表示成AoN (Activity-on-Node)网络,其中,节点代表活动,箭线代表活动之间的逻辑关系。现假定某一项目包含有N个活动,出于网络表述的需要,额外添加两个虚活动:活动0和活动N+1,前者表示项目的开始,后者表示项目的结束。项目的执行需要K种可更新资源,第k(k=1, 2,…,K)种资源的可用量为aK。活动i(i=0, 1,…,N+1)具有Mi种执行模式,以模式m(m=1, 2,…,Mi)执行时的工期为dim,对第k种资源的需求量为rikm。注意,虚活动0和N+1在任何执行模式下的工期及对资源的需求量均为0。
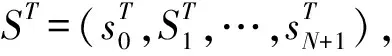
显然,在对项目进度计划进行调整时,应对BT中各活动的开始时间进行审慎的权衡和分析,以使得由此所引起的总损失Π最小化。
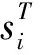
2 模型构建
根据上述对研究问题的界定,可构建基于资源随机中断的反应性多模式项目调度优化模型如下所述:
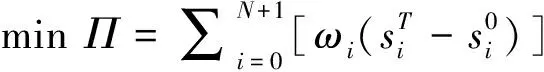
(1)
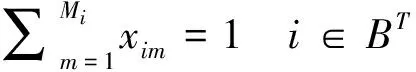
(2)
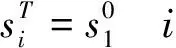
(3)
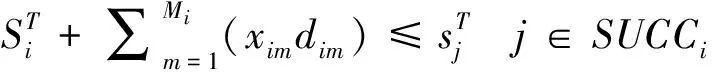
(4)

(5)
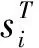
(6)
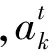
上述优化模型为一整数规划优化模型。目标函数式(1)最小化由于项目进度计划反应性调整而引起的总损失Π。约束条件式(2)为每个T时刻未完成的活动重新确定一种执行模式;式(3)将T时刻已经完成的活动的开始时间定义为基准开始时间;式(4)确保在对活动开始时间和执行模式进行调整时,活动之间的优先关系得到满足;式(5)为可更新资源约束,确保T时刻及其后每个时刻正在进行的活动对资源的总需求量不超过资源的可用量;式(6)为决策变量的定义域约束。
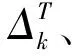
上述优化模型可视为经典的确定型资源约束项目调度问题(resource-constrained project scheduling problems)[11],向资源随机中断的不确定条件下的一种扩展,属于活动具有多种执行模式的资源约束反应性项目调度问题[12]。不失一般性,令模型中的Mi=1(i=0, 1,…,N+1),则本文所研究问题即可简化为一个单模式的资源约束反应性项目调度问题。也就是说,前者可视为后者在活动具有多种执行模式下的一般化形式,而后者则可视为前者在活动仅具有一种执行模式下的一个特例。由于单模式资源约束反应性项目调度问题已被Leus和Herroelen[13]证明为一NP-hard问题,所以,本文所研究问题也必然为一NP-hard问题。
3 算法设计
鉴于本文所研究问题的NP-hard属性,采用启发式算法求解该问题。已有相关研究[12,14]表明,禁忌搜索算法具有较优的计算效果,且该种算法已被众多学者[5~8]应用于反应性调度问题的求解中,因此本文也采用禁忌搜索对问题进行求解。本文所设计的禁忌搜索启发式算法具有如下特点:
采用活动优先次序列表表示问题的可行解,邻点生成操作简便易行;
所有生成的邻点中选择目标值较高的邻点进行移动,移动方向具有较强的确定性;
用禁忌列表对新近搜索过的移动进行禁止,避免陷入局部最优并减少重复搜索;
终止条件综合考虑搜索次数和无改进迭代次数,在保证解的质量的同时可减少无效搜索时间。
下面首先介绍算法的初始可行解构造、邻点生成机理、移动定义,然后给出禁忌列表、算法终止条件及具体的搜索步骤。
3.1 解的表示及初始解构造
问题的可行解用如下两个列表表示:
活动执行模式列表ML:该列表中的元素与集合BT中的活动一一对应,并按活动的编号次序排列,元素的取值定义了相应活动的执行模式。
活动优先次序列表AL:该列表定义了集合BT中活动在安排开始时间时的优先次序,即在不违反活动之间逻辑关系的前提下,排在该列表前面的活动优先考虑安排。给定一个AL,利用SSGS(serial schedule generation scheme)[15],可以生成一个唯一的满足资源约束的活动开始时间安排ST。
问题的初始可行解按下述步骤构造:
步骤1 随机地为BT中的每个活动选定一种执行模式,由此得到一个初始活动执行模式列表MLini。
步骤2 对于BT中的活动,在不违反活动之间逻辑关系的前提下,按照ωi取值从大到小进行排列,由此获得一个初始活动优先次序列表ALini。
3.2 邻点生成机理
当前可行解MLcur、ALcur的邻点MLnei、ALnei由如下算子生成:
执行模式改变算子MC:在MLcur上选择一个元素,将其取值改变成另外一个可行的取值,从而将其所代表活动的执行模式从当前模式转变为另一种模式,由此得到当前解的一个邻点(注意,在此过程中ALcur保持不变)。按照上述处理方式,MLcur上被选择的元素取值可以改变为任何其他可行的取值,而且,对于MLcur上的所有其他元素,均可做同样的处理。经过上述操作,可以获得当前可行解的一个邻点集合,在该集合中每个邻点的ML列表上,仅有一个元素的取值与当前解不同。
活动位置交换算子AS:在ALcur上选择两个元素,在不违反优先关系的前提下交换它们的位置,从而将当前可行解转变为它的一个邻点(注意,在此过程中MLcur保持不变)。按照上述处理方式,ALcur上任何两个无逻辑关系的元素均可做同样的处理,由此可获得当前可行解的一个邻点集合,在该集合中每个邻点的AL列表上,仅有两个元素的位置与当前解不同。
从上述算子生成的邻点集合中,选择最好的解(即目标函数值最小的解)作为当前可行解的邻点MLnei、ALnei。
3.3 移动定义
对应于生成邻点操作所使用的不同算子,相应的移动定义如下:
MC移动:用一个三元向量——(在MLcur上所选元素的位置,该元素的初始值,该元素的新值)。举例说明,如果MLcur上位置8的元素取值由2变成了1,那么MC移动表示为(8,2,1),其含义是位置8上元素所对应活动的执行模式由2变成了1。该移动的逆向移动表示为(8,2)并被同时加入到禁忌列表中,以避免位置8上的元素取值重新变回2。
AS移动:用一个二元向量——(在ALcur上所选的第1个元素的取值,在ALcur上所选的第2个元素的取值)表示。举例说明,如果ALcur上取值为5的元素与取值为7的元素互换位置,则AS移动表示为(5,7),其含义是取值为5的元素的优先次序与取值为7的元素的优先次序被互相交换。该移动的逆向移动表示为(7,5)并被同时加入到禁忌列表中,以避免取值为7的元素和取值为5的元素重新换回原来的位置。
3.4 禁忌列表及算法终止条件
禁忌列表的长度设置为[0.5NBT](其中,NBT为集合BT中活动的总数),采用“先进先出FIFO(First-in-First-out)”的原则进行管理:每当邻点生成算子形成一个移动时,该移动的逆向移动从底部加入到禁忌列表中,与此同时,最早进入列表的逆向移动从顶部移出列表,列表中其余逆向移动向上递进一位。所有位于禁忌列表中的逆向移动都是被禁止的,但当一个被禁止的逆向移动能够生成比当前最好解还要好的邻点时,它的禁忌状态可依据激活准则被解除,即将其从禁忌列表中删除,其下所有逆向移动向上递进一位,同时将该逆向移动加入到禁忌列表的底部。
在算法运行过程中,当下述两个终止条件有一个满足时,算法便停止搜索并将保存的当前最好解输出为满意解:
当搜索的邻点数Num达到Numstop,Numstop在本研究中设定为[100NBT];
算法的无改进迭代次数NNum达到NNumstop,且当前所有搜索对象均被禁忌,又不可激活,NNumstop在本研究中设定为[10NBT]。
3.5 搜索步骤
步骤1 输入初始可行解MLini、ALini,及其对应的目标值Πini。初始化禁忌列表,定义终止条件Numstop和NNumstop,令Num=0,NNum=0。将当前解及当前最好解赋值为初始解:MLcur=MLopt=MLini,ALcur=ALopt=ALini,Πcur=Πopt=Πini。
步骤2 从两个算子中随机地选择一个,生成当前解的邻点MLnei、ALnei,对应的目标函数值记为Πnei。判断生成该邻点的移动是否位于禁忌列表中,若是转步骤4;若否转步骤3。
步骤3 将当前解更新为邻点解:MLcur=MLnei,ALcur=ALnei,Πcur=Πnei。令Num=Num+1,更新禁忌列表。若Πnei<Πopt,进一步将当前最好解也更新为邻点解:MLopt=MLnei,ALopt=ALnei,Πopt=Πnei,令NNum=0。转步骤5。
步骤4 判断Πnei<Πopt是否成立。若成立则激活生成该邻点移动的禁忌状态,将当前解及当前最好解同时更新为邻点解:MLcur=MLopt=MLnei,ALcur=ALopt=ALnei,Πcur=Πopt=Πnei,令Num=Num+1,NNum=0,更新禁忌列表,转步骤5;否则,令NNum=NNum+1,转步骤6。
步骤5 判断Num≥Numstop是否成立。若成立转步骤7;否则,转步骤2。
步骤6 判断NNum≥NNumstop是否成立。若成立转步骤7;否则,转步骤2。
步骤7 输出当前最好解,即MLopt、ALopt、Πopt。
4 算法测试
为测试本文所设计的禁忌搜索启发式算法,用基准列表(活动优先次序列表按基准进度开始时间从小到大排列,活动模式与基准进度一致)和随机生成RG(random generation,即随机产生规定数目的可行解,从中选出最好解作为问题的满意解)两种启发式算法作为对比参照。随机生成的终止条件与禁忌搜索相同,即当探测可行解的总数达到Numstop时停止搜索。算法测试在ProGen[16]随机生成的标准算例上进行,算例的参数设置见表1。其中,按全因子实验设置的参数有4个:项目非虚活动数N、网络复杂度NC(network complexity,表示每个节点上无冗余的活动数平均值)、可更新资源强度RRS(renewable resource strength)和资源中断次数Numdis。其中,参数N和NC取值为3种,RRS和Numdis取值为4种,每种参数组合下生成的算例数为10个,由此得到3×3×4×4×10=1440个算例。以项目总工期最短为目标搜索得到的满意解作为项目的基准进度计划。算法绩效用如下四个指标进行评价:平均计算时间Timave、最大计算时间Timmax、平均目标函数值Пave和最大目标函数值Пmax。注意,在项目执行过程中,资源随机中断的发生有可能不止一次。当这种情况出现时,用多次资源中断算法运行结果的平均值作为相应的评价指标。上述三种算法均采用Visual C++6.0编程,在CPU为1.60GHz,内存为1.00GB的个人计算机上运行。
算法的测试结果如表2所示。由表2可见,对于全部算例,从获得的满意解质量看,禁忌搜索的Пave和Пmax比基准列表的相应指标分别低21.3%和10.2%,比随机生成的分别低50.6%和48.1%;从算法的运行时间看,由于基准列表算法没有搜索过程,因此Timave和Timmax近似为0;随机生成算法在搜索过程中不需要禁忌和判断,因此Timave和Timmax比禁忌搜索的低82.8%和93.1%。上述结果表明,在满意解质量方面,禁忌搜索最好,基准列表次之,随机生成最差;在计算时间方面,基准列表最好,随机生成次之,禁忌搜索最差。但是,算法的最长运行时间不超过4.3秒,所以,可以认为:在可接受的计算时间范围内,禁忌搜索启发式算法能够获得质量较高的满意解,与其他两种启发式算法相比,该算法是求解本文所研究问题的较好算法。
上述结果验证了本文所设计的禁忌搜索启发式算法的特点。首先,由于上述三种算法均采用优先次序列表生成活动的开始时间,因此搜索速度均较快。如果采用其他方式(如开始时间窗)搜索开始时间,禁忌搜索中AS算子的搜索范围将会大大扩大,必然会导致搜索时间的增加。其次,与基准列表算法和随机搜索算法相比,禁忌搜索的满意解质量最高,这与算法搜索时总是向目标值较高的邻点移动,保证了移动方向具有较强的确定性有关。而且,采用禁忌列表可使得搜索不局限在已经得到的最好解上,从而有效避免了陷入局部最优并减少了重复搜索,这也进一步提高了算法的搜索效率。最后,与一般禁忌搜索算法通常将搜索次数设定为终止条件不同,本文所设计的禁忌搜索算法同时考虑了无改进迭代次数,由此减少了无效的搜索时间,从而使得算法获得较为理想的计算结果。
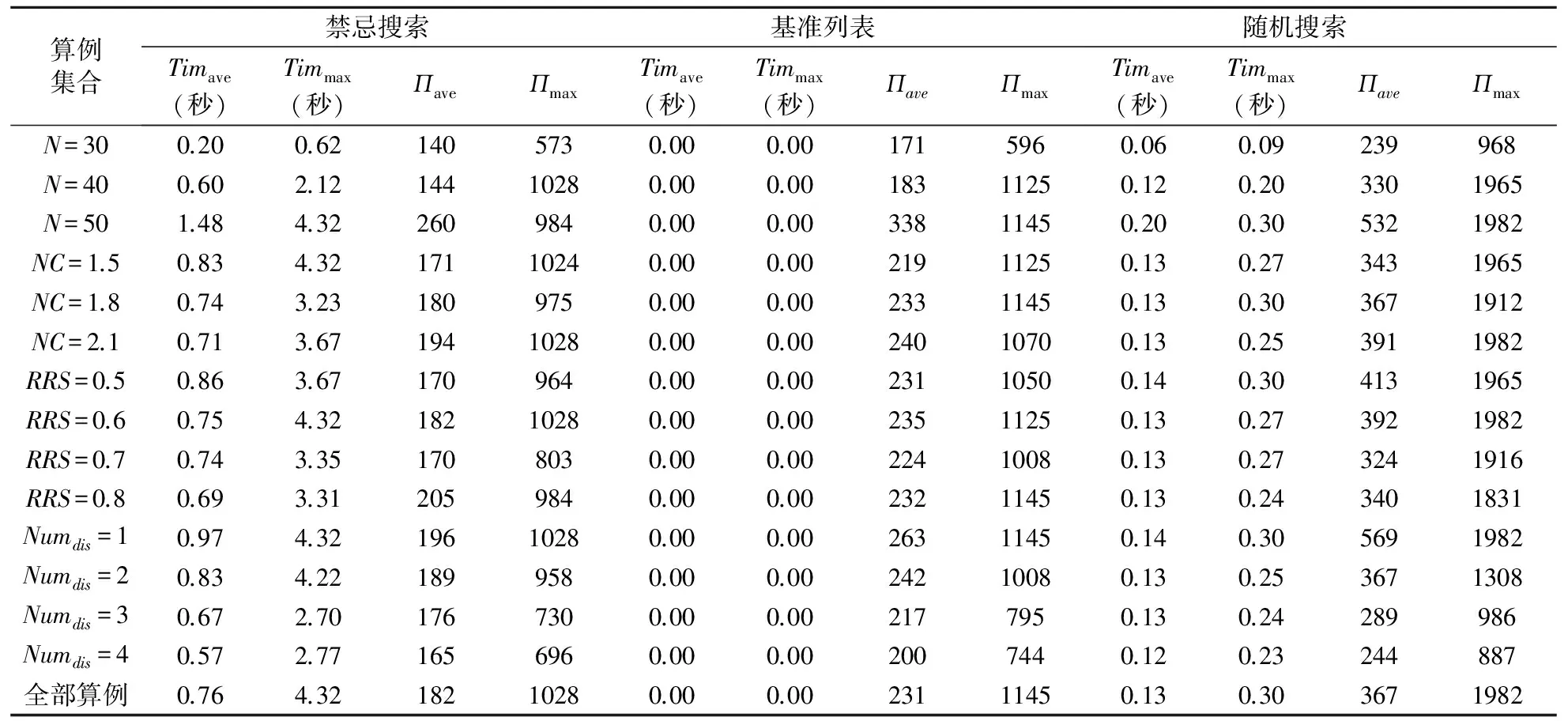
表2 算法的测试结果
从关键参数对运算时间Timave和满意解质量Пave的影响看,当算例规模N增大时,算法的Timmax和Пave单调上升。这是因为随着算例规模的增大,每次资源中断时需要调整的活动数随之增加,导致算法的计算时间变长,同时因活动开始时间延迟而引起的损失增加。当网络复杂度NC增大时,算法的Timave单调下降,Пave单调上升。造成这一结果的原因是:网络复杂度增加后,活动间的逻辑关系变复杂,一个活动延迟将影响更多的后续活动,所以资源中断造成的损失值增加,同时由于活动间优先关系变复杂,搜索的可行解变少,因而计算时间变短。当资源中断次数Numdis增大时,算法的Timmax和Пave单调下降。这主要是因为随着资源中断次数的增加,在给定项目规模的条件下,平均每次中断需要调整的活动数下降,所以,算法的计算时间变短,每次资源中断的平均额外总成本下降。
可更新资源强度RRS对计算结果的影响较为复杂。当RRS增大时,算法的Timave单调下降,而Пave却呈现随机波动的现象。这一结果分析如下:资源强度增大意味着活动安排时受到的资源约束放松,这使得在生成邻点的操作中资源约束更容易得到满足,因此计算时间也相应缩短。当资源约束放松时,满意解通常应该有所改善,但本文的测试结果却未支持这一结论。这是因为本文所采用的基准进度计划是以项目总工期最短为目标搜索得到的满意解,因此资源强度越大,基准进度计划越接近最优解,这样,当资源中断发生时,调整后的进度计划与基准计划的偏离便可能越显著;相反,当资源强度较小时,基准进度计划可能是一个距离最优解较远的满意解,这使得它反而对资源中断所造成的影响不是很敏感,亦即调整后的进度计划与基准计划偏离可能会较小。
5 结论
本文研究了基于资源随机中断的反应性多模式项目调度问题。作者首先对研究问题进行界定,目标是当资源中断发生时,在可更新资源约束下,合理安排活动的执行模式和开始时间,以最小化资源中断所造成的损失。在此基础上构建了问题的优化模型,并针对其NP-hard属性和特点设计禁忌搜索启发式算法。最后以基准列表算法和随机生成算法为参照,在随机生成的标准算例集合上对算法进行了比较测试,分析了项目活动数、网络复杂度、资源强度和资源中断次数等关键参数对计算结果的影响,得到如下结论:
在可接受的计算时间范围内,禁忌搜索启发式算法获得的满意解质量明显高于其他两种启发式算法,是求解本文所研究问题的较好算法;
算法的平均计算时间,随着项目活动数的增加而增加,随着网络复杂度、资源强度或资源中断次数的增加而减小;
满意解平均目标函数值,随着项目活动数或网络复杂度的增加而增加,随着资源中断次数的增加而减小,与资源强度无明显关系。
[1] 庞南生,孟俊姣.多目标资源受限项目鲁棒调度研究[J].运筹与管理,2012,21(3):27-32.
[2] Herroelen W, Leus R. Project scheduling under uncertainty: survey and research potentials[J]. European Journal of Operational Research, 2005, 165(2): 289-306.
[3] Vonder S V D, Demeulemeester E, Herroelen W. A classification of predictive-reactive project scheduling procedures[J]. Journal of Scheduling, 2007, 10: 195-207.
[4] Vonder S V D, Ballestin F, Demeulemeester E, Herroelen W. Heuristic procedures for reactive project scheduling[J]. Computers & Industrial Engineering, 2007, 52: 11-28.
[5] Deblaere F, Demeulemeester E, Herroelen W, Vonder S V D. Robust resource allocation decisions in resource-constrained projects[J]. Decision Sciences, 2007, 38(1): 5-34.
[6] Lambrechts O, Demeulemeester E, Herroelen W. Proactive and reactive strategies for resource-constrained project scheduling with uncertain resource availabilities[J]. Journal of Scheduling, 2008, 11: 121-136.
[7] Deblaere F, Demeulemeester E, Herroelen W. Reactive scheduling in the multi-mode RCPSP[J]. Computers & Operations Research, 2011, 38: 63-74.
[8] 任世科,袁治平,徐渝.突发事件应急救援动态调度优化: 以KX井喷事故为例[J].运筹与管理,2012,21(3):1-7.
[9] Mehta S, Uzsoy R. Predictive scheduling of a job shop subject to breakdowns[J]. IEEE Transactions on Robotics and Automation, 1998, 14: 365-378.
[10] Mehta S, Uzsoy R. Predictive scheduling of a single machine subject to breakdowns[J]. International Journal of Computer Integrated Manufacturing, 1999, 12: 15-38.
[11] Blazewicz J, Lenstra J K, Rinnooy K A H G. Scheduling subject to resource constraints: classification and complexity[J]. Discrete Applied Mathematics, 1983, 5: 11-24.
[12] Herroelen W, Leus R. Robust and reactive project scheduling: a review and classification of procedures[J] International Journal of Production Research, 2004, 42(8): 1599-1620.
[13] Leus R, Herroelen W. The complexity of machine scheduling for stability with a single disrupted job[J]. Operations Research Letters, 2005, 33(2): 151-156.
[14] Ouelhadj D, Petrovic S. A survey of dynamic scheduling in manufacturing systems[J]. Journal of Scheduling, 2009, 12: 417- 431.
[15] Kolisch R. Serial and parallel resource-constrained project scheduling methods revisited: theory and computation[J]. European Journal of Operational Research, 1996, 90(2): 320-333.
[16] Kolisch R, Sprecher A. PSPLIB-aproject scheduling problem library[J]. European Journal of Operational Research, 1996, 96(1): 205-216.
Optimization of Reactive Multi-mode Project Scheduling Based on Stochastic Breakdown of Resources
LI Jia-yuan, HE Zheng-wen
(SchoolofManagement,Xi’anJiaotongUniversity,Xi’an710049,China)
Resource breakdown occurs frequently during the implementation of projects. It may lead to the changes of project schedule and generate additional expenses. This paper involves the project scheduling problem under resource breakdown, where the objective is to adjust the baseline schedule reasonably so as to minimize the incurred additional expenses. The problem is identified at first and the optimization model is constructed accordingly. For the NP-hardness of the problem, a tabu search heuristic algorithm is developed. Finally, given the baseline list algorithm and the random generation algorithm as comparison, we test the tabu search algorithm on a set of standard instances generated randomly. The conclusions are drawn as follows. First, within the acceptable computation time, the quality of the desirable solutions obtained by the tabu search heuristic algorithm is significantly better than those obtained by other two heuristic algorithms. Second, the average computation time increases with the activity number, but decreases with the network complexity, the renewable resource strength, and the number of resource breakdown, respectively. Third, the mean of objective function value also climbs with the activity number and drops with the network complexity and the number of resource breakdown, but it seems that there is no significance influence on the renewable resource strength.
reactive project scheduling; optimization model; tabu search; stochastic resource breakdown
2012- 08-12
国家自然科学基金资助项目(70971105、71371150);新世纪优秀人才支持计划资助项目(NCET-13- 0460)
李佳媛(1987-),女,青海西宁人,硕士研究生,研究方向:项目管理及优化。
C935;F224.33
A
1007-3221(2015)06- 0044- 07
10.12005/orms.2015.0194
