基于动态参照点的损失厌恶投资组合优化模型
2015-06-07王佳,金秀,苑莹,王旭
王 佳, 金 秀, 苑 莹, 王 旭
(1.东北大学 工商管理学院,辽宁 沈阳 110819; 2.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
基于动态参照点的损失厌恶投资组合优化模型
王 佳1, 金 秀1, 苑 莹1, 王 旭2
(1.东北大学 工商管理学院,辽宁 沈阳 110819; 2.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
在连续时间下,考虑损失厌恶投资者参照点的动态调整特征,构建基于动态参照点的损失厌恶投资组合模型,使用鞅方法对模型进行求解,得到最优风险资产权重的解析表达式。并计算损失厌恶投资者在参照点动态调整条件下的预期最优期末财富。进一步应用数值算例,分析投资者的参照点动态调整幅度和损失厌恶水平对模型最优风险资产权重和预期最优期末财富的影响。
动态参照点;损失厌恶;投资组合;连续时间
0 引言
预期效用理论是研究不确定性决策问题的著名理论,描述理性经济人在风险条件下的决策行为。但研究表明,该理论不能有效地解释金融市场上的各种异象[1,2]。一些学者认为这是由于人类的认知、情感等心理因素严重地影响投资者的决策行为。Kahneman等[3]从认知心理学的角度提出前景理论,指出投资者利用一定的参照水平衡量收益和损失,且具有损失厌恶特征,对损失比对盈利更敏感。
国内外一些学者对基于损失厌恶的投资组合模型进行研究。文献[4-6]分析有限离散时间下损失厌恶投资者的最优投资组合选择,不能解决关于投资者投资决策的动态控制问题。一般来说,投资组合选择模型分为离散时间和连续时间模型两大类。任何离散时间模型下的时间间隔都不足以反应金融市场状态瞬息万变的特征。而连续时间模型能够将股票价格的动态变化与时间连续变化的随机过程相联系,比离散时间模型更接近实际[7]。Berkelaar等[8]将Merton提出的连续时间投资组合理论与前景理论相结合,研究投资者的损失厌恶心理对资产定价的影响。Jin等[9]在完全市场框架下从累积前景理论的角度构建行为投资组合模型,并将模型分为正部问题和负部问题分别进行求解,得到最优期末财富的显式解。De Giorgi等[10,11]在连续时间下的损失厌恶投资组合模型中引入狭窄框架思想,并分析不同损失厌恶效用函数和概率加权对投资组合选择的影响。Rásonyi等[12]研究连续时间下损失厌恶投资组合模型的适定性问题。Yao等[13]指出市场的不完全信息导致了投资者损失厌恶和乐观的心理特征,并在此基础上得到损失厌恶投资者的最优资产配置策略。米辉等[14]在完全市场框架下研究当财富值具有基准下限约束时的损失厌恶投资组合模型。
以上学者的研究都假设整个投资期投资者的参照点保持恒定。Barberis[15]和Zhang等[16]指出由于私房钱效应和盈亏平衡效应的存在,投资者前一阶段的收益和损失会影响当前阶段的参照水平,进而对投资者的效用产生影响。Berkelaar等[17]研究损失厌恶投资者的最优资产配置策略,并指出由于市场具有随机不确定性,损失厌恶投资者用于衡量盈利和损失的参照点会经常随着财富状况和时间的变化而动态更新。因此,考虑投资者在投资过程中对参照点的动态调整,研究动态参照点下的损失厌恶效用更符合投资者的真实心理。
本文以文献[17]参照点的动态调整思想为基础,考虑连续时间下损失厌恶模型的适定性问题,构建基于动态参照点的损失厌恶投资组合模型,使用鞅方法对模型进行求解得到最优风险资产权重的解析表达式,并在此基础上计算投资者的预期最优期末财富。进一步应用数值算例,分析参照点的动态调整幅度和损失厌恶水平对模型的影响。
1 模型
1.1 基本假定
假设一个连续时间的完全市场,投资者以初始财富W0∈R+投资于K+1种资产,投资期为T∈R+。t时刻第k种资产的价格为Sk(t),k=0,…,K,t∈[0,T]其中第0种资产是无风险资产,价格的动态变化过程为
dS0(t)=r(t)S0(t)dt
(1)
其余资产是风险资产,价格变化遵循伊藤过程
(2)
r(·)为即期利率,μ(·)=(μ1(·),…,μK(·))′和σ(·)=(σkl(·))K×K分别为漂移率向量和波动率矩阵,表示风险资产的瞬时条件期望收益率和标准差,B(t)=(B1(t),…,BK(t))′为K维标准布朗运动,k,l=1,…,K。
完全市场中存在唯一的状态价格密度ξ(t),表达式为
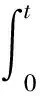
(3)
且ξ(t)具有以下特征
①
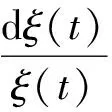
(4)
②
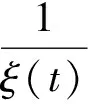
(5)
③ 在市场参数μ(·)、σ(·)和r(·)为常数的条件下,ξ(t)服从对数正态分布,均值和方差分别为
E(ln(ξ(t)))=mt,Var(ln(ξ(t)))=s2t
(6)
在允许卖空的条件下,ω(t)表示t时刻风险资产的权重向量,则投资者财富W(t)的动态变化过程为
dW(t)=r(t)W(t)dt+(μ(t)-1r(t))′ω(t)W(t)dt+σ(t)′ω(t)W(t)dB(t)
(7)
1.2 模型构建
Kahneman 和Tversky提出S形损失厌恶效用函数,表达式为
(8)
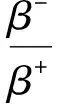
整个投资期,损失厌恶投资者的参照点不是恒定的,而是随着财富状况和无风险收益的变化而动态变化[9]
d(θ(t))=υdW(t)+(1-υ)θ(0)r(0)dt,0<υ<1
(9)
在式(8)和(9)的基础上得到基于动态参照点的损失厌恶效用函数
(10)
θT(υ)为动态参照点,表达式为
θT(υ)=θ(0)+υ(W(T)-W(0))+(1-υ)θ(0)r(0)T,0<υ<1
(11)
其中,初始财富W(0)、初始参照点θ(0)和无风险利率r(0)均为常量,υ为参照点受财富变动影响的系数。风险资产的存在使组合财富的变动幅度大于无风险收益的变动。因此,υ越接近1,表明参照点的动态调整幅度越大;υ越接近0,表明参照点的动态调整幅度越小。
在式(10)的基础上,以动态投资者的预期损失厌恶效用最大化为目标函数,考虑连续时间下损失厌恶模型的适定性问题,引入财富的动态变化方程和非负约束,构建基于动态参照点的损失厌恶投资组合模型
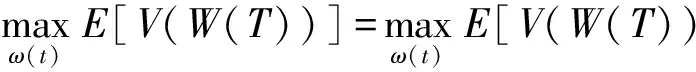
(12)
s.t. dW(t)=r(t)W(t)dt+(μ(t)-1r(t))′ω(t)W(t)dt+σ(t)′ω(t)W(t)dB(t)
(13)
W(t)≥0,t∈[0,T]
(14)
其中,风险资产的权重向量ω(t)为决策变量,式(13)为财富的动态变化过程,式(14)表示整个投资期财富值非负。财富值非负的约束条件使连续时间下的损失厌恶模型具有适定性[14],因此求解模型(12)~(14)时不需要再加入额外的假设就可以得到最优解。
1.3 模型求解
首先,利用鞅方法[18]将连续时间下的损失厌恶模型(12)~(14)转化为求解最优期末财富的静态模型;其次,利用鞅的性质对最优期末财富进行复制得到模型的最优解,即投资者的最优风险资产权重。为便于求解,设投资者投资于一种风险资产和一种无风险资产,具体计算过程为:
第一步,利用鞅方法,将模型(12)~(14)转化为以最优期末财富W(T)为决策变量的静态损失厌恶投资组合模型

(15)
s.t.E[ξ(T)W(T)]≤ξ(0)W0
(16)
W(T)≥0,t∈[0,T]
(17)
其中,式(16)为用鞅方法表示的预算约束方程,ξ(T)为投资期的状态价格密度。
第二步,对模型(15)~(17)进行求解。由于目标函数不是全局凹函数,不能直接使用数学规划法。因此,分别考虑凹函数和凸函数两部分,并利用库恩-塔克最优化条件得到模型的最优解,见定理1。
定理1 具有动态参照点的损失厌恶投资者最优期末财富为
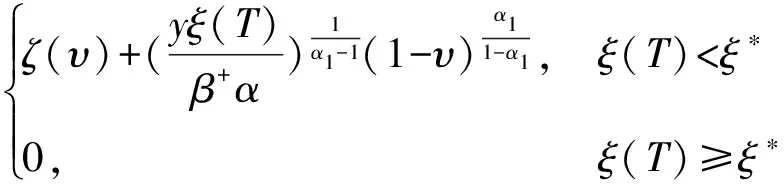
(18)
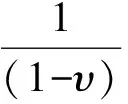
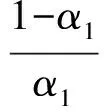
第三步,利用鞅的性质对最优期末财富式(18)进行复制得到模型(12)~(14)的最优解,即损失厌恶投资者的最优风险资产权重,见定理2。
定理2 具有动态参照点的损失厌恶投资者最优风险资产权重为
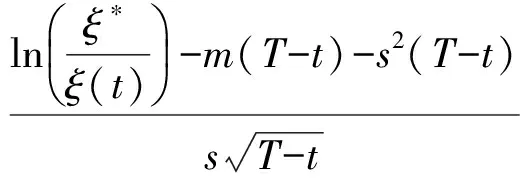
1.4 预期最优期末财富
为研究基于动态参照点的损失厌恶模型的表现,在定理1的基础上计算投资者的预期最优期末财富,见定理3。
定理3 具有动态参照点的损失厌恶投资者预期最优期末财富为
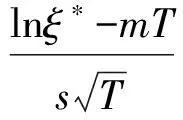
证明 由定理1得
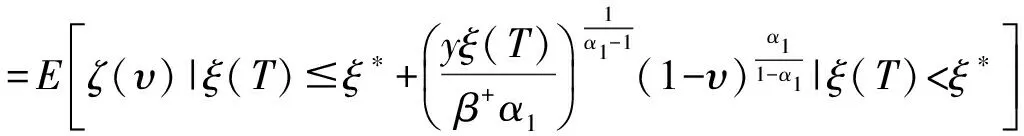
(19)
由式(6)得,服从对数正态分布,均值和方差分别为
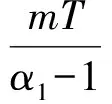
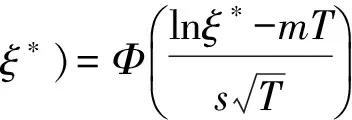
(20)
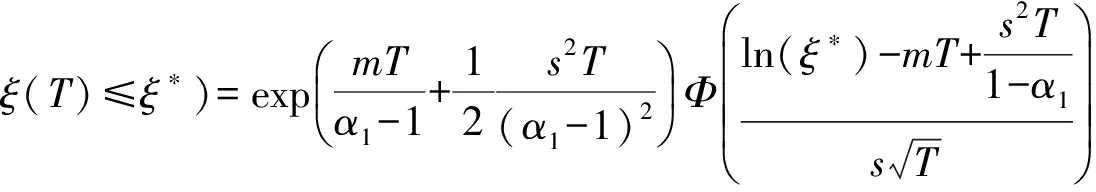
(21)
将式(20)和(21)代入式(19),得到具有动态参照点的损失厌恶投资者预期最优期末财富
证毕。
2 算例
假设无风险利率r=0.03,风险市场价格κ=0.2,风险资产的标准差σ=10%,投资者的初始财富W(0)=1,损失厌恶参数β+=1,收益和损失的曲率参数α1=α2=0.88,初始参照点θ(0)=1.03。
受投资经验、心理预期及对市场的认知程度等各种主观因素影响,不同投资者的参照点动态调整幅度和损失厌恶程度可能会有所不同。因此,设参照点受财富变动影响的系数υ分别为0.2、0.5和0.8,表示参照点不同的动态调整幅度,损失厌恶参数β-分别为1.5、2.25和3,表示不同的损失厌恶水平。
2.1 最优风险资产权重
由定理2可以看出,其他参数一定的条件下,最优风险资产权重ω(t)是状态价格密度ξ(t)的连续函数,即损失厌恶投资者持有的最优风险资产权重与市场状态有关。投资者的参照点动态调整幅度不同和不同的损失厌恶水平对最优风险资产权重ω(t)的影响如图1~图6所示。设投资期T=1,t=0.5。

图1 最优风险资产权重比较 (β-=1.5) 图2 最优风险资产权重比较 (β-=2.25) 图3 最优风险资产权重比较(β-=3)

图4 最优风险资产权重比较(υ=0.2) 图5 最优风险资产权重比较(υ=0.5) 图6 最优风险资产权重比较(υ=0.8)
从图1~图6可以看出,随着状态价格密度ξ(t)增大,损失厌恶投资者的最优风险资产权重呈“V”形。具体表现为:①当ξ(t)较小时,市场状态较好,投资者风险厌恶水平较低,从而持有较高的风险资产权重;②当ξ(t)较大时,市场状态较差,盈亏平衡效应的存在[16],使投资者具有较高的风险偏好水平,仍然持有较高的风险资产权重。
(1)参照点的动态调整幅度对最优风险资产权重的影响
从图1~图3可以看出,相同的损失厌恶水平下,参照点的动态调整幅度对投资者最优风险资产权重的影响与市场状态有关。具体表现为:①当ξ(t)较小时,市场状态较好,系数v较小即参照点的动态调整幅度较小的投资者持有较高的风险资产权重;②当ξ(t)较大时,市场状态较差,系数υ较大即参照点的动态调整幅度较大的投资者持有较高的风险资产权重;③损失厌恶水平越大,系数υ变动对最优风险资产权重的影响越明显。
(2)损失厌恶水平对最优风险资产权重的影响
从图4~图6可以看出,系数υ一定的条件下,β-值较小即损失厌恶水平较低的投资者持有的风险资产权重较高。
2.2 预期最优期末财富
由定理3可以看出,其他参数一定的条件下,预期最优期末财富E(W*(T))是投资期T的连续函数,即损失厌恶投资者的预期最优期末财富与投资期有关。投资者的参照点动态调整幅度不同和不同的损失厌恶水平对预期最优期末财富E(W*(T))的影响如图7~图12所示。
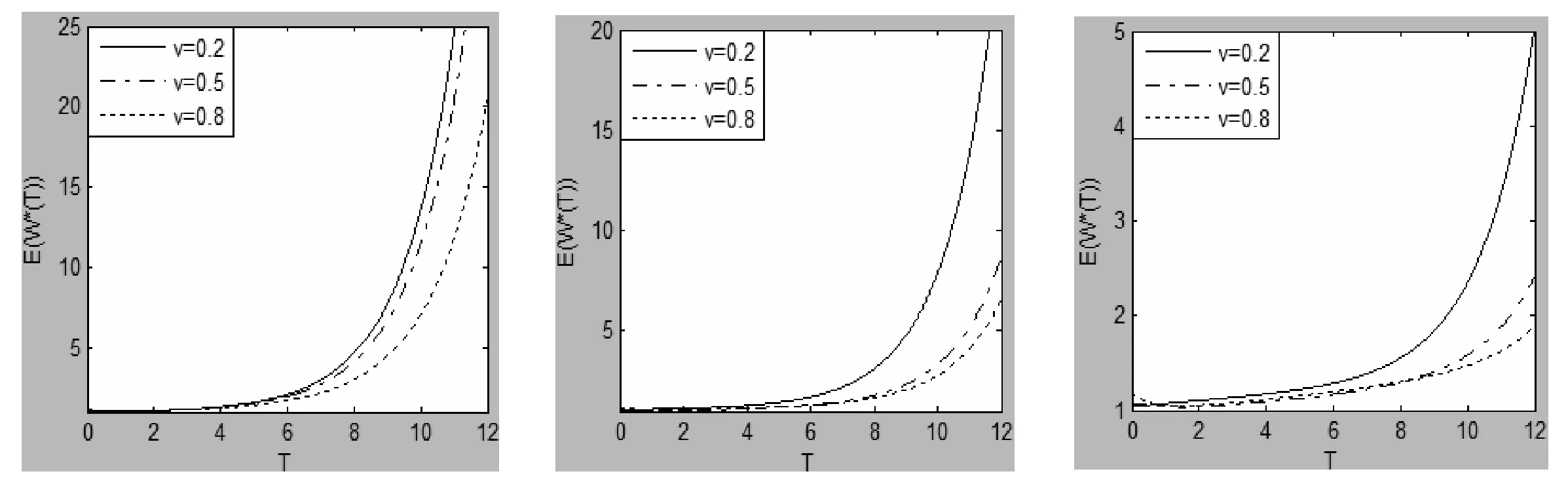
图7 预期最优期末财富比较(β-=1.5) 图8 预期最优期末财富比较(β-=2.25) 图9 预期最优期末财富比较(β-=3)
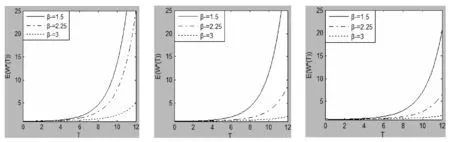
图10 预期最优期末财富比较(υ=0.2) 图11 预期最优期末财富比较(υ=0.5) 图 12预期最优期末财富比较(υ=0.8)
从图7~图12可以看出,随着投资期增加,损失厌恶投资者的预期最优期末财富逐渐增加。
(1)参照点的动态调整幅度对预期最优期末财富的影响
从图7~图9可以看出,损失厌恶水平一定的条件下,参照点的动态调整幅度对投资者预期最优期末财富的影响与投资期有关。具体表现为:①在中短期投资中,系数v不同,投资者的预期最优期末财富差别不大;②在长期投资中,系数υ较小即参照点的动态调整幅度较小的投资者具有较高的预期最优期末财富。
(2)损失厌恶水平对预期最优期末财富的影响
从图10~图12可以看出,系数υ一定的条件下,损失厌恶水平对投资者预期最优期末财富的影响与投资期有关。具体表现为:①在中短期投资中,不同损失厌恶水平下投资者的预期最优期末财富差别不大;②在长期投资中,β-较小即损失厌恶水平较低的投资者具有较高的预期最优期末财富值。
3 结论
构建连续时间下基于动态参照点的损失厌恶投资组合模型,使用鞅方法对模型进行求解得到最优风险资产权重的解析表达式,并计算投资者在参照点动态调整条件下的预期最优期末财富。进一步应用数值算例,分析投资者的参照点动态调整幅度和损失厌恶水平对动态模型的影响。得出以下结论
(1)从最优风险资产权重的比较结果可以看出,投资者的最优投资决策与当前市场状态、参照点的动态调整幅度和损失厌恶程度均相关。①相同的损失厌恶水平下,当市场状态较好时,参照点的动态调整幅度较小的投资者持有较高的风险资产权重;反之当市场状态较差时,参照点的动态调整幅度较大的投资者持有较高的风险资产权重;②参照点的动态调整幅度一定时,损失厌恶水平较低的投资者持有较高的风险资产权重。这说明机构投资者和投资咨询机构在指导投资者进行投资时,应明确当前市场状态,并根据投资者对参照点的不同偏好和不同的损失厌恶程度制定出符合特定投资者的最优投资决策。
(2)从预期最优期末财富的比较结果可以看出,投资者的投资绩效与参照点的动态调整幅度、损失厌恶程度和投资期均相关。①相同的损失厌恶水平下,投资期越长,参照点的动态调整幅度对预期最优期末财富的影响越明显,且长期投资中参照点的动态调整幅度较小的投资者具有较高的预期最优期末财富;②参照点的动态调整幅度一定时,投资期越长,损失厌恶水平变动对预期最优期末财富的影响越明显,且长期投资中损失厌恶水平较低的投资者具有较高的预期最优期末财富。这说明长期投资中,投资者对参照点的不同偏好和不同的损失厌恶程度能够在一定程度上影响其投资绩效。
[1] Benartzi S,Thaler R H. Myopic loss aversion and the equity premium puzzle[J]. Quarterly Journal of Economics, 1995, 110(1): 73-92.
[2] Siegel J, Thaler R H. Anomalies: the equity premium puzzle[J]. Journal of Economic Perspectives, 1997, 11(1): 191-200.
[3] Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291.
[4] Gomes F J. Portfolio choice and trading volume with loss-averse investors [J]. Journal of Business, 2005, 78(2): 675-706.
[5] Pirvu T A, Schulze K. Multi-stock portfolio optimization under prospect theory[J]. Mathematics and Financial Economics, 2012, 6(4): 337-362.
[6] Fortin I, Hlouskova J. Optimal asset allocation under linear loss aversion[J]. Journal of Banking and Finance, 2011, 35(11): 2974-2990.
[7] Merton R C. The financial system and economic performance[J]. Journal of Financial Services Research, 1990, 4(4): 263-300.
[8] Berkelaar A, Kouwenberg R. From boom ‘til bust: how loss aversion affects asset prices[J]. Journal of Banking and Finance, 2009, 33(6): 1005-1013.
[9] Jin H Q, Zhou X Y. Behavioral portfolio selection in continuous time[J]. Mathematical Finance, 2008, 18(3): 385- 426.
[10] De Giorgi E G. Loss aversion with multiple investment goals[J]. Mathematics and Financial Economics, 2011, 5(3): 203-227.
[11] De Giorgi E G, Legg S. Dynamic portfolio choice and asset pricing with narrow framing and probability weighting[J]. Journal of Economic Dynamics and Control, 2012, 36(7): 951-972.
[12] Rásonyi M, Rodrigues A M. Optimal portfolio choice for a behavioral investor in continuous-time markets[J]. Annals of Finance, 2013, 9(2): 291-318.
[13] Yao J, Li D. Bounded rationality as a source of loss aversion and optimism: a study of psych-ological adaptation under incomplete information[J]. Journal of Economic Dynamic and Control, 2013, 37(1): 18-31.
[14] 米辉,张曙光.财富约束条件下损失厌恶投资者的动态投资组合选择[J].系统工程理论与实践,2013,33(5):1107-1115.
[15] Barberis N, Huang M. Mental accounting, loss aversion, and individual stock returns[J]. Journal of Finance, 2001, 56(4): 1247-1292.
[16] Zhang W, Semmler W. Prospect theory for stock markets: empirical evidence with time-series data[J]. Journal of Economic Behavior and Organization, 2009, 72(3): 835- 849.
[17] Berkelaar A, Kouwenberg R, Post T. Optimal portfolio choice under loss aversion[J]. The Review of Economics and Statistics, 2004, 86(4): 973-987.
[18] Harrison J M, Pliska S R. Martingales and stochastic integrals in the theory of continuous trading[J]. Stochastic processes and their applications, 1981, 11(3): 215-206.
Loss Aversion Portfolio Optimal Model with Dynamic Reference Point
WANG Jia1, JIN Xiu1, YUAN Ying1, WANG Xu2
(1.CollegeofBusinessAdministration,NortheasternUniversity,Shenyang110819,China; 2.CollegeofInformationScience&Engineering,NortheasternUniversity,Shenyang110819,China)
Under continuous time, considering dynamic updating character of reference point of loss aversion investors, we construct loss aversion portfolio model with dynamic reference point. Then, using martingale method, we derive the analytical expression of optimal risky asset weight, based on which we obtain the expected optimal terminal wealth of loss aversion investors whose reference point is dynamically adjusted. Furthermore, using numerical cases, we analyze the effects of dynamic adjustment amplitude of reference point and loss aversion degree of investors on model from the aspects of optimal risky asset weight and expected optimal terminal wealth.
dynamic reference point; loss aversion; portfolio; continuous time
2014- 04-17
国家自然科学基金资助项目(71271047,70901017)
王佳(1986-),女,河北唐山人,博士,讲师,研究方向:金融工程、行为金融;金秀(1963-),女,辽宁辽阳人,教授,博士生导师,研究方向:金融工程、行为金融。
F830
A
1007-3221(2015)06- 0051- 07
10.12005/orms.2015.0195
