子阵级和差波束形成及测角方法研究

杨雪亚，刘张林

（中国电子科技集团第38研究所孔径阵列与空间探测安徽省重点实验室，合肥 230088）

子阵级和差波束形成及测角方法研究

杨雪亚，刘张林

（中国电子科技集团第38研究所孔径阵列与空间探测安徽省重点实验室，合肥 230088）

大型面阵采用子阵级波束形成降低了计算量和接收通道数，由于只有一套功分网络，无法有效抑制差波束的副瓣。针对单脉冲相控阵系统，在子阵级采用数字加权抑制差波束的副瓣，使用虚拟子阵差波束的加权系数对子阵级输出进行幅度修正，改善了差波束的副瓣性能。基于对称取反的子阵级差波束形成，提出了改进的基于正弦空间坐标系的和差波束测角误差曲线建立及方法，对不同频率及不同波束指向只需建分别立方位和俯仰各一条误差曲线，降低了查表运算量和数据存储需求。仿真结果验证了本文方法的可行性和有效性。

子阵；低副瓣；和差波束；测角

0 引 言

数字波束形成（Digital Beam Forming，DBF）技术是一种在数字域实现波束形成的技术，它保留了天线阵列单元信号的全部信息，并可采用先进的数字信号处理技术对阵列信号进行处理，可以获得优良的波束形成性能［1，2］。在现代雷达系统中，为了增强探测威力、提高角度测量精度，一般雷达天线含有数百乃至上万个阵元，很难在阵元级上采用数字波束形成方法。通常对大型阵列进行子阵的划分，子阵内采用模拟移相器进行波束形成，子阵间采用数字波束形成，极大地减少了接收所需的通道数，节约了硬件成本。

国内外在子阵级波束形成方面做了大量的研究，Nickel从子阵级和差波束方向图性能的角度提出了一种基于锥削函数量化的子阵划分方法［3］。Ferrier［4］比较了一种平面阵的非均匀与均匀邻接子阵结构，结论是前者的自适应方向图没有栅瓣，但副瓣电平较高。许志勇在文献［5，6］分别提出了等子阵加权法和等噪声功率法，按照不同子阵内加权系数之和或者加权系数平方之和相等的原则划分子阵，显著改善了波束的副瓣性能。近年来，优化方法［7-9］在子阵划分中得到了应用，然而，受限于T／R组件和功分网络的结构，实际中往往不能对天线阵列任意分割子阵，尤其是大型二维面阵，因此仅依靠优化子阵分割方式提高波束的性能是不可取的。相控阵雷达采用单脉冲测角技术，必须同时形成和、差波束，子阵模拟合成时只有一套功分网络，无法通过全阵元处理时幅度加权的方式同时形成和、差波束用于测角。针对设定的子阵分割方式，胡航［10-12］研究了通过二级子阵加权的方法改善差波束的副瓣，第一级子阵加权用以抑制差波束副瓣，第二级子阵加权对子阵输出进行幅度预处理。这些方法主要考虑均匀线阵的第一级子阵加权抑制差波束副瓣，涉及十分繁琐的运算过程，显然不利于工程实现，而且无法简单推广至二维平面阵。

针对二维平面阵，对和波束及方位、俯仰差波束分别进行幅度归一化预处理，在不增加运算量的前提下改善了差波束的副瓣性能；给出了一种改进的基于子阵级的对称取反法和、差波束形成方法，并提出了一种正弦空间坐标系的角度误差曲线建立方法，将误差信号对频点和波束指向进行归一化，在方位和俯仰向分别建立一条误差曲线，减小了误差曲线存储量。

1 阵列模型

如图1所示的平面阵，方位向和俯仰向最大阵元数分别为Ny和Nz，阵元间距分别为dy和dz，Na个单元分成Ns个子阵，所有子阵在4个象限呈对称分布，每个子阵的阵元数为Nci（i＝1，2，…，Ns）。以面阵中心为参考点，若接收波束指向为（θ0，φ0），则位于阵列第nz行ny列的单元天线的相移表示为

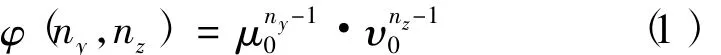
对于第i个子面阵，维数为Nci的子阵模拟合成

图1 子阵划分示意图

变换行向量ti定义为

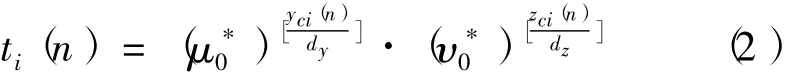
其中yci（n）和zci（n）分别为第i个子面阵的第n个阵元的两维坐标，［·］表示向下取整。因此，面阵的子阵合成矩阵为

若阵元接收信号为Na×1的列向量x，则式（3）的子阵变换矩阵可实现对面阵的子阵内部合成，形成Ns个数字通道数据y＝Tsx，然后进行子阵间数字波束形成。

为了得到较好的副瓣效果，采取幅度加权，方位和俯仰加权向量分别为wy和wz，则式（3）修正为

通常wy和wz分别为方位向和俯仰向的Taylor幅度加权系数。

2 子阵级和差波束形成

全数字波束形成时，通过幅度加权实现和、差波束，即和波束采用Taylor幅度权，方位及俯仰差波束分别采用Bayliss幅度权［13］。但是对于子阵级数字波束形成，只有一套模拟合成网络，无法直接使用Bayliss权形成差波束。就是说，在一级子阵合成时加一组和波束的幅度权系数，而方位及俯仰差波束只能通过对子阵级输出进行数字加权形成。本方案采取对称取反的方式形成差波束，如图1所示面阵分为16个子阵，子阵合成数据为yi，i＝1～16，定义子阵级的和波束及方位和俯仰差波束加权系数BΣ、Bθ，Δ和Bφ，Δ如下：

和波束、方位差波束及俯仰差波束的合成信号分别为

由于子阵内一级合成时阵元数目不同且幅度加权系数差别较大，导致子阵输出的噪声功率有差异，引起和、差波束方向图的副瓣抬高，不利于目标检测，同时也会影响测角精度。采用子阵幅度修正的预处理方法，每个子阵所用幅度加权值为子阵内所有阵元的幅度加权值的能量和的倒数，即

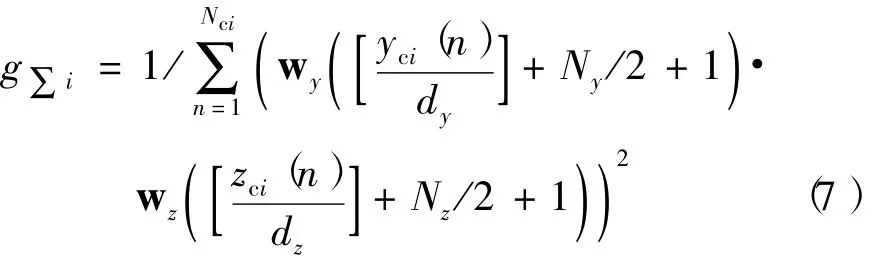
利用列向量gΣi对子阵合成输出进行预处理，形成和波束向量yΣ

幅度预处理后，所有子阵输出的能量将近似保持一致，减弱了子阵内加权系数的差异引起的副瓣电平抬高的问题。

对于方位及俯仰差波束，考虑面阵为全数字阵列时每个子阵内虚拟的差波束加权系数，并在子阵级差波束形成时用虚拟的子阵差波束加权系数对子阵输出进行幅度修正，在子阵二级加权体现出与全数字阵列差波束形成相对应的信号和噪声能量关系。假设仍然通过Bayliss权形成差波束，方位和俯仰的Bayliss权分别为wdy和wdz，计算形成方位及俯仰差波束所在每个阵元上的幅度权：

因此，每个子阵分别形成方位及俯仰差波束时所有阵元的幅度加权值的能量和为

形成差波束时利用式（12）进行幅度修正

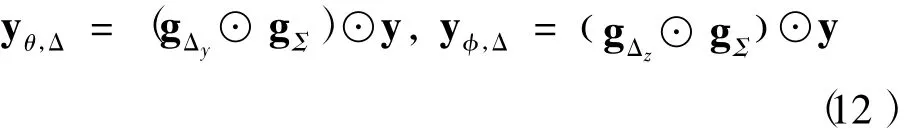
由于式（9）-（10）所需的幅度修正因子可以离线计算并存储，对计算资源要求较低。通过对差波束的预处理，使得子阵级差波束在子阵级别上与全数字阵列的输出能量保持一致。

3 子阵级和差波束测角方法

和差波束测角不仅具有较高的测量精度，而且实现简单，因此受到了广泛的关注和应用。在给定频率f0（波长为λ0）、目标角度为（θT，φT）、波束指向为（θ0，φ0）的情况下，子阵级和波束、方位差波束及俯仰差波束接收的信号如式（6）所示。

计算方位和俯仰归一化误差信号，定义方位归一化误差信号Eθl如式（13）所示

类似地，可得俯仰角归一化误差信号Eφl

当目标两维角度（θT，φT）在以波束指向为中心的波束宽度内变化时，就建立了一个波束宽度范围内和方位角及俯仰角一一对应的误差信号EθT和EφT，形成方位和俯仰的误差曲线表。通过计算方位和俯仰误差信号，并查找误差曲线表，得到目标偏离波束指向大小Δθ及Δφ，并根据式（15）估计目标的方位角和俯仰角

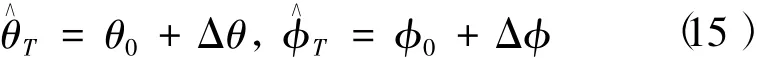
但是两维和差波束需要在不同频点、不同的方位和俯仰波束指向处建立误差曲线并存储，测角时选取对应的误差曲线查表。对不同的信号波长λ和接收波束二维指向（θ0，φ0），需要建立多个误差曲线表，当雷达工作频点和波位排布较多时，工作量和存储量非常可观。而且，和、差波束在角度上不具有平移性，当扫描角较大时，波束方向图发生畸变，导致测角性能恶化。

研究给出了在正弦空间坐标系（u-v）建表，并且考虑了频率因素，分别定义沿方位向和俯仰向的与波长（即频率）、波束方位和俯仰正（余）弦指向相关的变量u和v如下

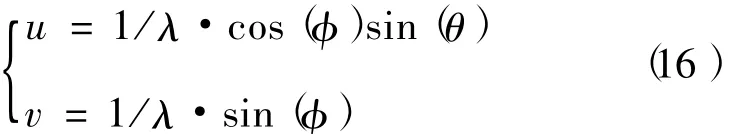
由于方位和俯仰误差曲线随u和v具有平移不变性，误差曲线的形状不随u和v变化，形成方位u和俯仰v两组误差曲线，适用于任何频点和二维波束指向。以波束宽度内的u和v建立误差曲线表，得到归一化误差曲线和u、v的关系。在实际测量时，由方位和俯仰归一化误差分别计算Δu和Δv，然后根据式（17）估计目标方位角和俯仰角。

4 仿真分析

对于图1所示的面阵，340个阵元在四个象限均分成4个子阵，子阵的阵元数分别为16、21、28、20，发射信号频率12 GHz，阵元间距dy＝dz＝0.5λ。方位和俯仰二维波束指向为（40°，30°），和波束采用-25 dB的Taylor幅度加权。方位和、差波束方向如图2所示，俯仰和、差波束方向如图3所示。结果表明，相比较未做幅度修正的差波束方向图，采用差波束幅度修正后，不仅有效降低了差波束方向图的副瓣（副瓣电平-16 dB左右），而且差波束方向图的形状保持良好，体现了本文给出的子阵级和差波束形成方法的优势。

图2 方位和、差波束方向图

图3 俯仰和、差波束方向图

基于以上仿真条件，比较传统的角误差信号建表方法在以下三种情况下的方位和、差波束的归一化误差曲线：频率为12 GHz、二维波束指向为（0°，0°），频率为11.5 GHz、二维波束指向为（0°，0°），频率为11.5 GHz、二维波束指向为（40°，30°），如图4所示。可见，不同频点、同一波束指向的归一化误差曲线不相同，相同频点、不同波束指向的归一化误差曲线也有差别，这就要求对不同的频率和波束指向建立多个误差表，必然带来复杂的查表运算和大量的数据存储。采用正旋空间建表，并对信号波长进行归一化，如图5所示，所有频点和波束指向的误差曲线重叠，基准频点和波束指向（可取12 GHz、（0°，0°））的一条误差曲线对不同频率和不同波束指向的二维角度测量均具有适用性。

图4 传统方法方位和、差波束归一化误差曲线

图5 本文方法方位和、差波束归一化误差曲线

5 结 语

对于平面阵子阵级数字和、差波束形成，子阵内模拟合成采用和波束幅度加权，因此子阵间数字加权形成的差波束方向图副瓣较高，影响目标检测及角度测量。本文通过虚拟阵元级波束形成的差波束加权系数对子阵输出进行幅度修正，对子阵加权系数的能量进行归一处理，并采用对称取反的方式形成差波束，在不增加计算复杂度的情况下改善了差波束副瓣性能。然后建立基于正弦空间的测角误差曲线，只需方位和俯仰两条曲线，可满足所有频点、所有二维波束指向的测角需求，降低了查表复杂度并节约了存储空间。仿真结果表明了其相对于传统子阵级波束形成及测角方法的良好性能。

［1］吴曼青.数字阵列雷达的发展与构想［J］.雷达科学与技术，2008，6（6）：401-405.

［2］朱庆明.数字阵列雷达述评［J］.雷达科学与技术，2004，2（3）：136-141.

［3］NICKEL U.Subarray Configurations for Digital Beamforming with Low Sidelobes and Adaptive Interference Suppression［C］.Proc of the IEEE international Radar Conference，Alexandria，USA，1995：714-719.

［4］FERRIER J M.Antenna Subarray Architectures and Anti-Jamming Constraints［C］.Proc of the IEEE International Radar Conference，Paris，France，1994：466-469.

［5］XU Z Y，BAO Z，LIAO G S.A Method of Designing Irregular Subarray Architectures for Partially Adaptive Processing［C］.IEEE International Radar Conference，Beijing，China，1996：460-463.

［6］许志勇，保铮，廖桂生.一种非均匀邻接子阵结构及其部分自适应处理性能分析［J］.电子学报，1997，25（9）：20-24.

［7］MICHELE D'Urso，TOMMASO I，ETTORE FM.An Effective Hybrid Approach for the Optimal Synthesis of Monopulse Antennas［J］.IEEE Trans.on AP，2007，55（4）：1059-1066.

［8］熊子源，徐振海，张亮等.阵列雷达最有子阵划分研究［J］.雷达科学与技术，2011，9（4）：370-377.

［9］LOPEZ P，RODRIGUEZ JA，ARES F，et al.Subarray Weighting for the Difference Patterns ofMonopulse Antennas：Joint Optimization of Subarray Configurations and Weights［J］.IEEE Trans.on AP，2001，49（11）：1606-1608.

［10］胡航，王泽勋，刘伟会.相控阵的两级子阵加权方法研究［J］.电波科学学报，2009，24（6）：1038-1043.

［11］胡航，刘伟会.只利用一种模拟加权的子阵级和差波束旁瓣抑制方法［J］.电子与信息学报，2009，31（4）：974-976.

［12］岳朝阳，雷丽丽，胡航.子阵级相控阵差波束旁瓣抑制新方法［J］.电波科学学报，2011，26（1）：14-17.

［13］SRINIVASA R Z，JEONG P K.On the Generalization of Taylor and Bayliss n-bar Array Distributions［J］.IEEE Trans.on AP，2012，49（11）：1152-1157.

杨雪亚（1984—），男，高级工程师，安徽省阜南人，博士研究生，主要研究方向为雷达信号处理和阵列信号处理；

E-mail：xueya_y＠126.com

刘张林（1975—），男，安徽省桐城人，硕士研究生，研究员，主要研究方向为雷达阵列信号处理、雷达信号处理应用及研究。

Research on Beam-form ing and Angle M easurement M ethod at Sub-array Level for Planar Array

YANG Xue-ya，LIU Zhang-lin
（Key Laboratory of Aperture Array and Space Exploration，the 38th Research Institute of CETC，Hefei230088，China）

In order to simplify the radar receiving system，sub-array beam-forming is used in large scale planar array radar.However，the side lobe of difference beam is relatively high because the only power divider network is used to sum beam.Aiming at the phased array radar system which appliesmonopulse technology，a digitalweighting technique is adopted to suppress side lobe of difference beam，and the virtual weights for sub-arrays are applied to correct the output of sub-arrays，which lowers the side lobe of difference beam.Furthermore，a difference beam-formingmethod based on negation of symmetric sub-arrays is given，and a novel angle-error-curve-builtmethod is presented，which builds one angle error curve for azimuth angle or elevation angle in sinusoidal space coordinate for all frequencies and beam pointing. The presented method reduces the computation complexity and memory needed by error curves.The simulation results verify the feasibility and effectiveness of themethod.

sub-array；low side lobe；sum and difference beam；anglemeasurement

TN958

：A

：1673-5692（2015）01-082-05

10.3969／j.issn.1673-5692.2015.01.014

2014-11-20

2015-01-19