经验小波变换在旋转机械故障诊断中的应用

向 玲， 李媛媛

（华北电力大学 机械工程系，河北保定071003）

机械故障信号一般为非平稳、非线性、非高斯信号，目前常用的时频分析方法主要包括短时傅里叶变换、Wigner－Ville分布、小波变换和经验模态分解等.然而，在现代信号处理方法中，短时傅里叶变换一旦选定了窗函数，其时频分辨率就固定不变了［1］，这不符合实际问题中高频信号分辨率应比低频信号分辨率高的要求.Wigner－Ville分布虽然具有很高的时域和频域分辨率，但对于多分量信号，由于交叉干扰项的存在，其应用受到了很大的限制［2］.小波变换虽然有多分辨率（即多尺度）的特性，可以由粗及细地逐步观察信号，但由于需要人为地选择小波基，因此缺乏自适应性［3］.经验模态分解（EMD）是Norden E Huang等在1998年提出来的，该方法可以将多分量的非平稳信号自适应分解为多个本征模态函数（IMF）分量，对单个分量进行Hilbert变换即可得到瞬时频率以及瞬时幅值.但是EMD 方法仍然存在许多问题，如过包络、欠包络、模态混叠和端点效应等［4－6］.经验小波变换（EWT）是Gilles［7］提出的一种新的信号处理方法，该方法对信号的傅里叶频谱进行划分，并建立一组小波滤波器组对划分过的频谱进行滤波得到一组单分量成分，与EMD 方法一样，其对每个单分量成分进行Hilbert变换即可得到瞬时频率和瞬时幅值，具有较大的应用价值.

为了验证所提出的经验小波变换的有效性，笔者针对仿真信号和转子系统实验故障信号将EWT方法与EMD 方法进行了比较研究，EWT 方法能准确地分析机械故障信号，故障特征值明显，为旋转机械故障诊断提供了一种新的手段.

1 经验小波变换

经验小波变换实际上就是对信号的傅里叶频谱进行划分，并建立一组适合待处理信号的小波滤波器.首先，对信号的傅里叶频谱进行划分，规定规范化的信号傅里叶频谱的频率范围为［0，π］.假设信号由N 个单分量成分组成，找到频谱图中的极大值，假设极大值个数为M，将这些极大值降序排列，则存在2种情况［7－8］：

（1）M≥N.此时该算法找到了足够的极大值，保留前N 个极大值.

（2）M＜N.此时信号包含的单分量个数小于期望的分量个数N，保留所有的极大值，并且对N 值进行重置.

综合考虑上述2 种情况并确定极大值个数之后，将频率范围为［0，π］的傅里叶频谱划分成N 个连续的区间，那么就需要确定N＋1条边界线，其中0和π分别为第一条和最后一条边界线，另外还需要再确定N－1条边界线.过ωn所在点作相邻2个区间的分界线，那么每一段可表示为Λn＝［ωn－1，ωn］，n＝1，2，…，N（ω0＝0，ωN＝π），其中，ωn为2个连续 的 极 大 值 的 中 点，由 此 可 知∪Nn＝1Λn＝［0，π］［9－10］.具体划分情况见图1，其中阴影部分表示以ωn为中心，宽度为2τn的过渡段，τn＝γωn，γ为系数.

图1 傅里叶坐标系分割图Fig.1 Partitioning of the Fourier axis

在确定分割区间Λn后，对其加小波窗，根据Meyer小波的构造方法，定义经验尺度函数和经验小波函数分别为：

其中，γ ＜minn［ωn＋1－ωn／ωn＋1＋ωn］，β（x）＝x4（35－84x＋70x2－20x3）.

根据经典小波变换的构造方法构造经验小波变换，细节系数和近似系数［11］分别为：

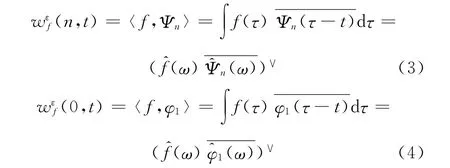
进行信号重构，重构结果如式（5）所示.

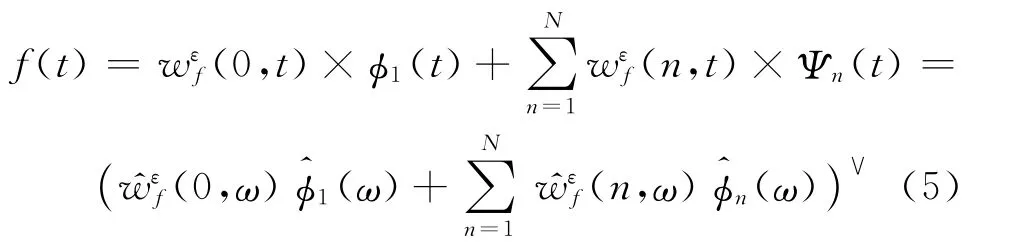
由以上公式得到经验模态函数fk，可由式（6）和式（7）表示：

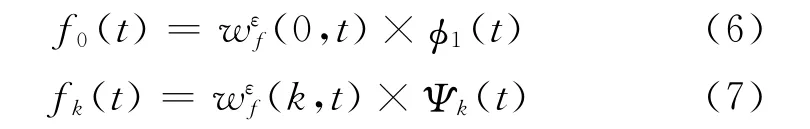
2 仿真信号分析

为了验证EWT 方法的有效性，并与EMD 方法进行简单的对比研究，首先对含随机噪声（式（8））的仿真信号x（t）进行分析处理，图2为该仿真信号的时域波形图.

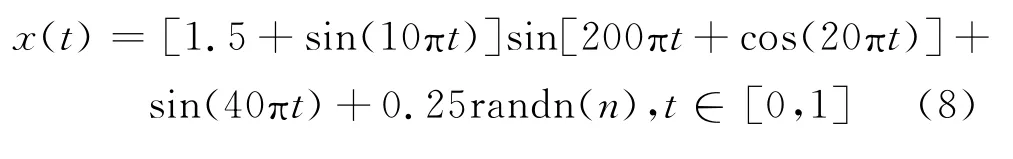
图2 仿真信号x（t）的时域波形图Fig.2 Time wave form of the signal x（t）

该仿真信号由一个调幅调频信号，一个频率为20Hz的sin信号以及一个标准差为0.25的随机噪声信号组成，分别利用EMD 方法和EWT 方法对该仿真信号进行时频分析，结果见图3和图4.

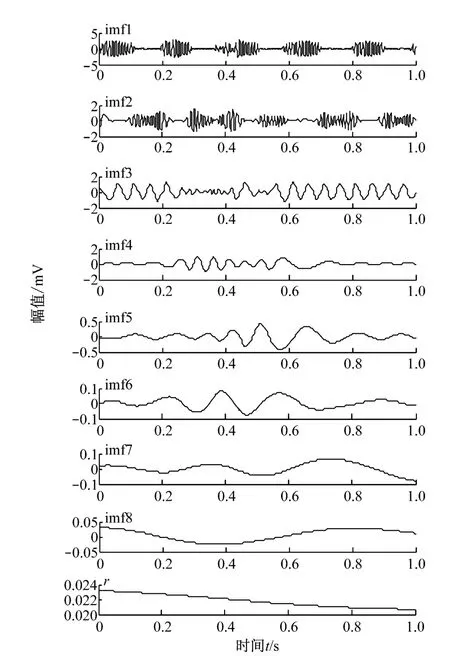
图3 仿真信号x（t）的EMD分解结果Fig.3 EMD result generated from the signal x（t）

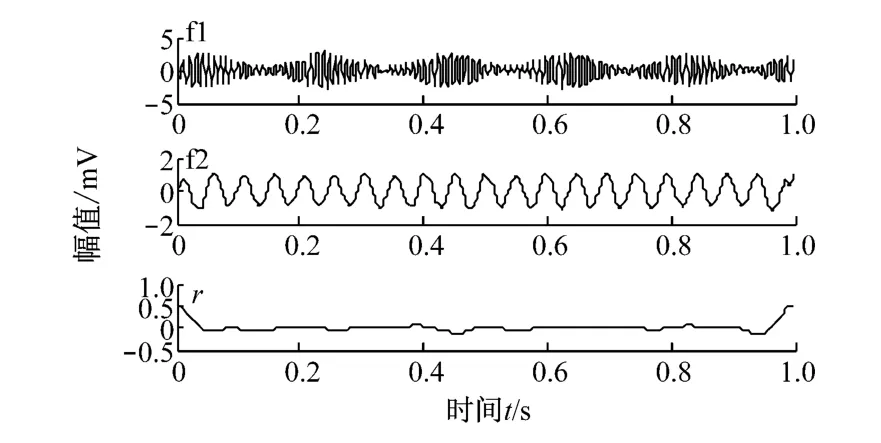
图4 仿真信号x（t）的EWT 分解结果Fig.4 EWT result generated from the signal x（t）

由图3和图4可知，由于仿真信号存在随机噪声，EMD 方法分解得到的前2个分量对应仿真信号中100Hz的调幅调频分量，模态混叠严重，信号分量不易辨识.而EWT 方法分解得到的前2个分量分别对应该仿真信号中100 Hz的调幅调频分量和20Hz的sin信号分量，且分量波形清晰，不存在混叠现象.通过对比发现，EMD 方法和EWT 方法均能对调幅调频信号进行分解，但是EMD 方法分解层数明显多于EWT 方法，且模态混叠现象严重，分解得到的残余分量比EWT 方法得到的残余分量波动大，提取的故障特征也没有EWT 方法明显.

3 实验信号分析

为了模拟转子故障信号，采用Bently模拟转子实验台作为模拟旋转机械故障的装置.Bently RK－4转子平衡实验台能够模拟实际的转子工况，因而能够模拟转子不平衡、转子碰磨和油膜涡动等故障.同时，采用ZonicBook／618E作为信号采集设备.

3.1 转子不平衡

转子不平衡实验采用涡流传感器，传感器布置情况为：圆盘两侧各2个，且呈90°夹角，键相传感器1只.在圆盘上涡流传感器之间45°角处加试重1g，调整转子的转速达到3 500r／min，测试不平衡振动.设置采样频率为1 280 Hz，通过数据采集设备，任意选取故障数据中的1 000个点，分析比较采集到的数据.

图5给出了转子不平衡信号的时域和频域图.由图5可知，转子不平衡［12］信号的时域波形为正弦信号的叠加，而在频谱图中，出现了58.88 Hz的基频分量和二倍频、三倍频等高频分量，但是倍频成分幅值都比较小，因此采用傅里叶变换（FFT 变换）不能充分证明故障是否发生.

图6和图7分别为EMD 方法和EWT 方法对转子不平衡信号分析处理的结果.从图6和图7可以看出，转子不平衡信号的基频为58.88 Hz，但在EMD 时频图中，基频成分存在调制现象，在0～0.6 s内模态混叠现象也比较严重.与EMD 时频图相比，EWT 时频图的频率值更清晰，二倍频成分被清楚地分解出来，模态混叠现象明显减轻，且端点效应也得到一定的抑制，故障特征明显.由此证明EWT方法故障特征提取效果显著.

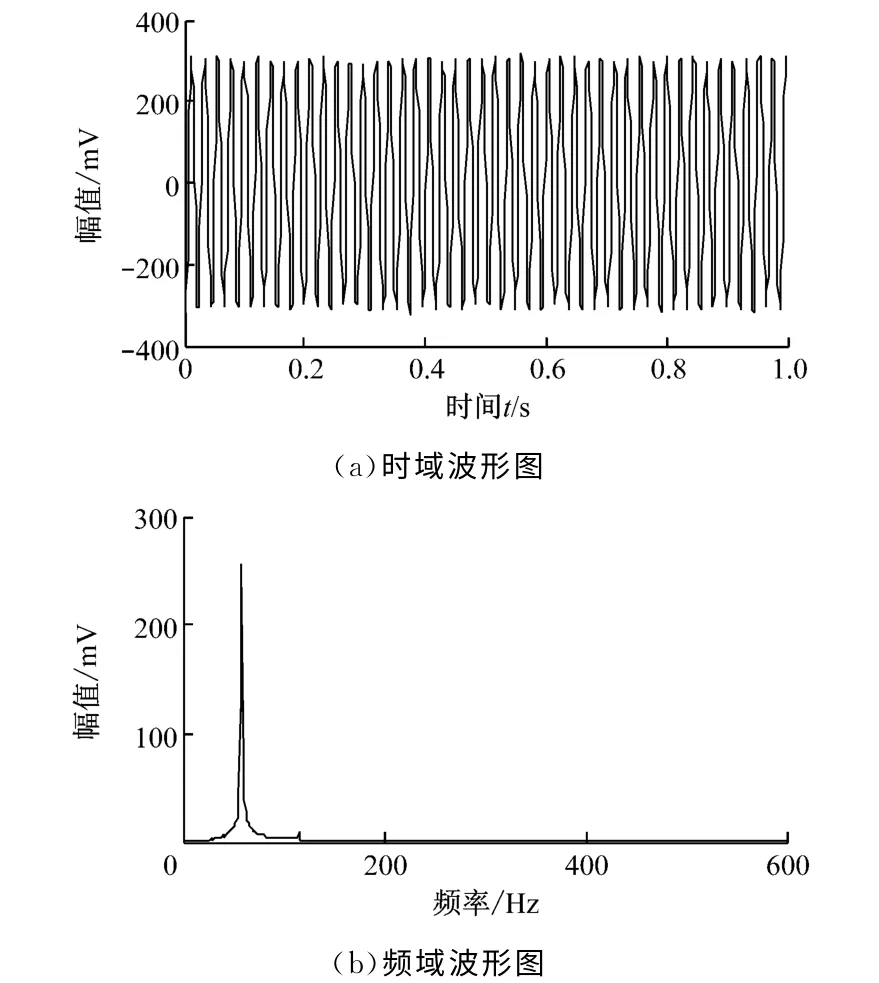
图5 转子不平衡信号的时域和频域波形Fig.5 Time and spectral diagram of rotor unbalance signals

图6 转子不平衡信号的EMD方法时频图Fig.6 Time－frequency spectrum of rotor unbalance signals based on EMD

图7 转子不平衡信号的EWT 方法时频图Fig.7 Time－frequency spectrum of rotor unbalance signals based on EWT

3.2 转子碰磨

转子碰磨实验采用涡流传感器，传感器布置如下：圆盘两侧各2 个，且呈90°夹角，键相传感器1只.调整转子的转速达到1 790r／min，固定塑料棒与轴的位置不变，用塑料棒与轴进行全周碰磨.设置采样频率为1 280 Hz，通过数据采集设备，任意选取故障数据中的1 000 个点，分析比较采集到的数据.

图8为转子碰磨信号的时域和频域图.由图8可以看出，转子碰磨［13］信号的时域波形为正弦信号的叠加，而在频谱图中，出现了30Hz的基频分量和二倍频、三倍频等高频分量，但是倍频成分幅值都比较小，不易从频谱图中分辨出来，因此采用FFT 变换不能充分证明故障是否发生.

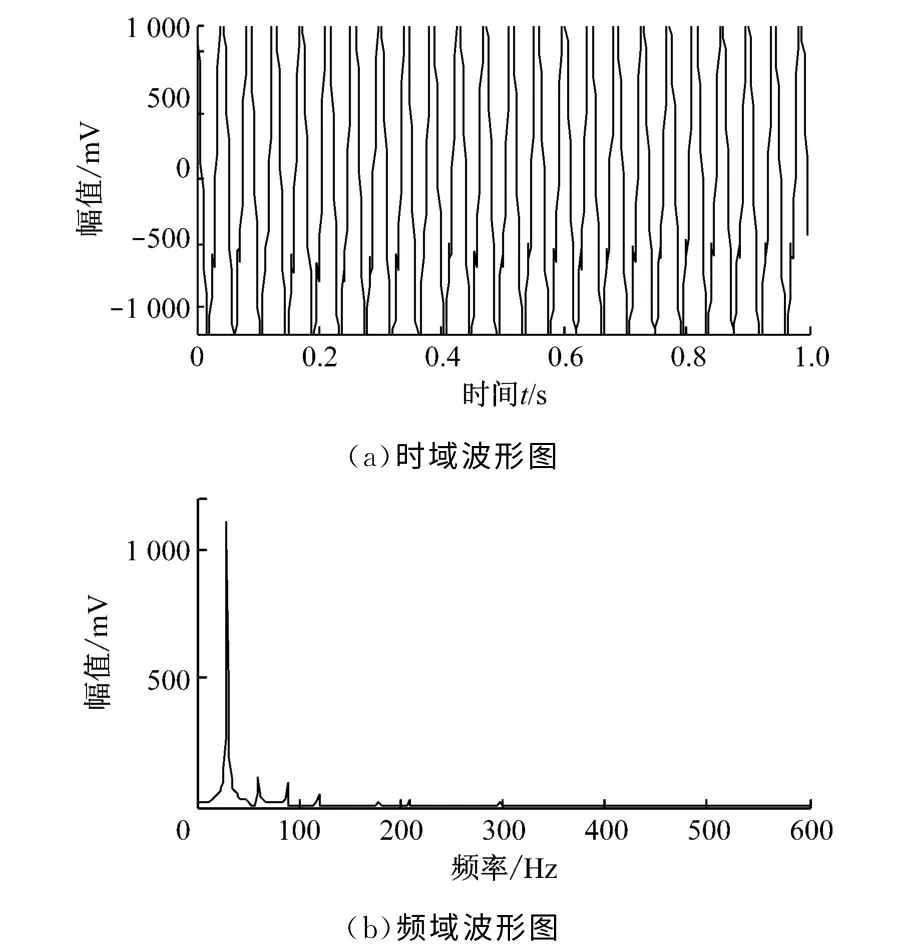
图8 转子碰磨信号的时域和频域波形Fig.8 Time and spectral diagram of rotor rubbing fault signals

图9 和图10分别为EMD 方法和EWT 方法对转子碰磨信号分析处理的结果.从图9和图10可以看出，转子碰磨信号的基频为30 Hz，但在EMD 时频图中，基频成分存在调制现象，模态混叠现象也比较严重.而EWT 时频图的频率值更加清晰，二倍频、三倍频等转子碰磨故障频率成分也被成功地分解出来，谱线清晰，模态混叠现象明显减轻，且端点效应也得到一定程度的抑制，提取得到的故障特征非常明显.由此证明EWT 方法效果显著.

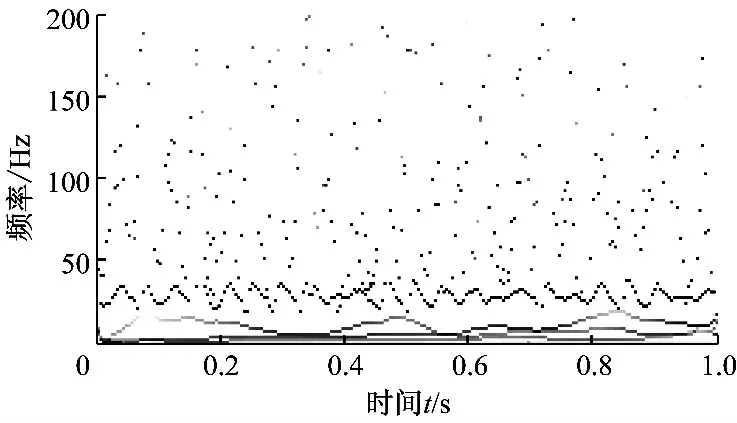
图9 转子碰磨信号的EMD方法时频图Fig.9 Time－frequency spectrum of rotor rubbing fault signals based on EMD

图10 转子碰磨信号的EWT 方法时频图Fig.10 Time－frequency spectrum of rotor rubbing fault signals based on EWT

3.3 油膜涡动和油膜振荡

油膜涡动故障发生时，会产生频率值为转子基频0.43～0.48倍的油膜涡动故障频率，且轴心轨迹呈内8字形.此时如果转子的转速继续升高，并且达到转子第一阶临界转速的2倍以上，油膜涡动故障频率就会达到第一阶临界转速，从而产生共振，振幅骤增，达到甚至超过基频振幅，从而发生油膜振荡［14］，此时由于转子振动剧烈，轴心轨迹杂乱，同时还会引起动静部件摩擦、转子热弯曲和瓦面碎裂等，具有较大破坏力.

3.3.1 油膜涡动

油膜波动实验采用涡流传感器，传感器布置如下：轴中部、油轴承上各2个，呈90°夹角，键相传感器1只.通过调节油泵、预紧力支架和调速电机控制器，使转子的转速达到3 500r／min，从而产生油膜涡动.设置采样频率为1 280 Hz，通过数据采集设备，任意选取故障数据中的1 000个点，分析比较采集到的数据.

图11给出了油膜涡动信号的时域图、频域图和轴心轨迹.由图11可知，油膜涡动故障信号的时域波形为正弦信号的叠加，在频域图中，出现了58.88 Hz的基频分量和略低于二分频的频率为28 Hz的油膜涡动故障频率，且故障频率幅值较基频幅值略低，与此同时，还出现了故障频率的三倍频.转子的轴心轨迹为内8字形状，大圈套小圈，由此可以判断为油膜涡动故障.但是仅凭频域图无法准确判断是否发生该故障.

图12和图13分别为EMD 方法和EWT 方法对油膜涡动信号分析处理的结果.从图12 和图13可以看出，油膜涡动故障频率为28 Hz，但是EWT方法还分解得到了信号的基频58.88 Hz，且EWT方法时频图谱线较EMD 方法时频图谱线清晰，模态混叠现象明显减轻，调制现象减弱，故障特征值明显，故障诊断效果显著.

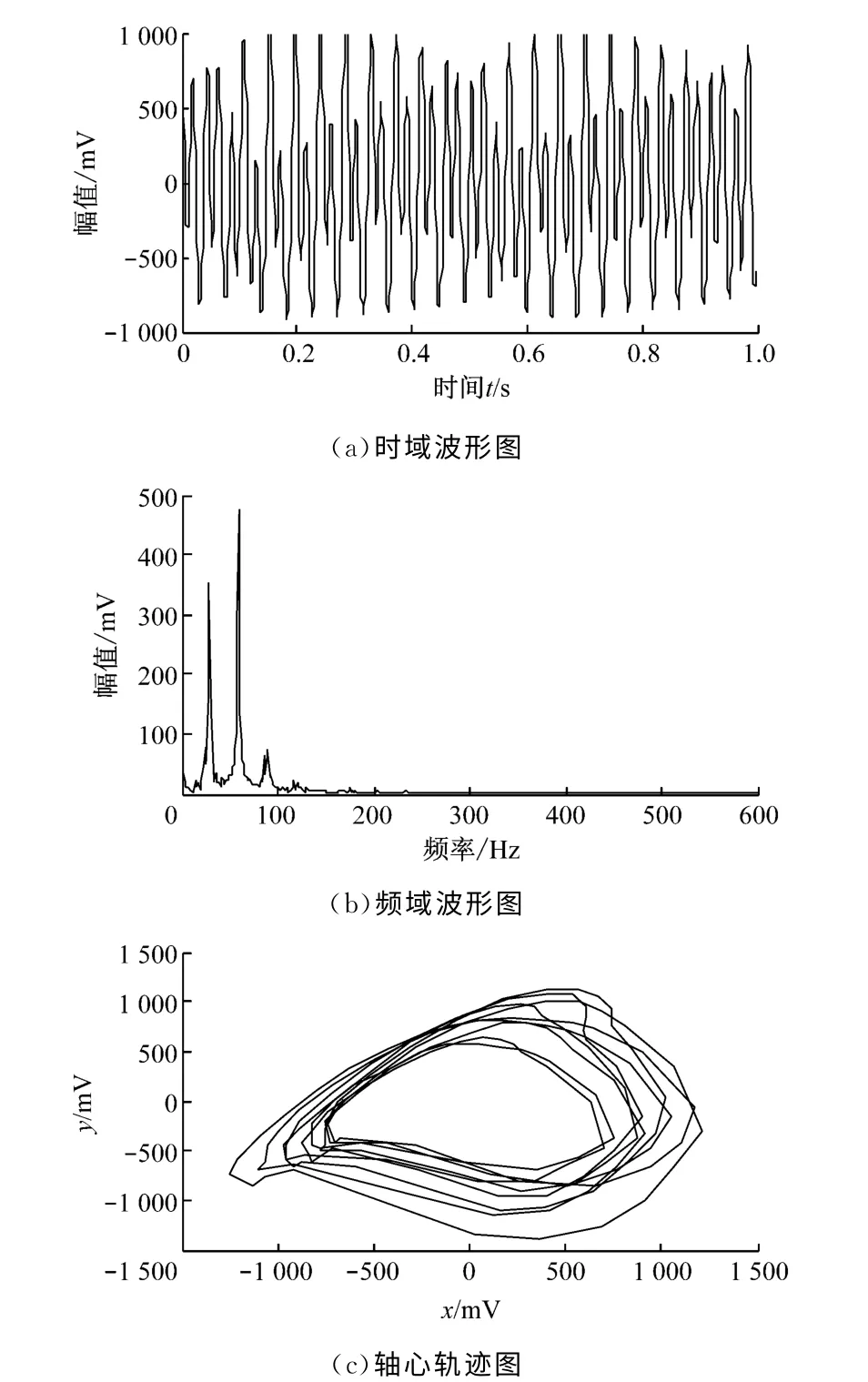
图11 油膜涡动信号的时域图、频域图和轴心轨迹Fig.11 Time wave form，spectral diagram and axis orbit of oil whirl signals

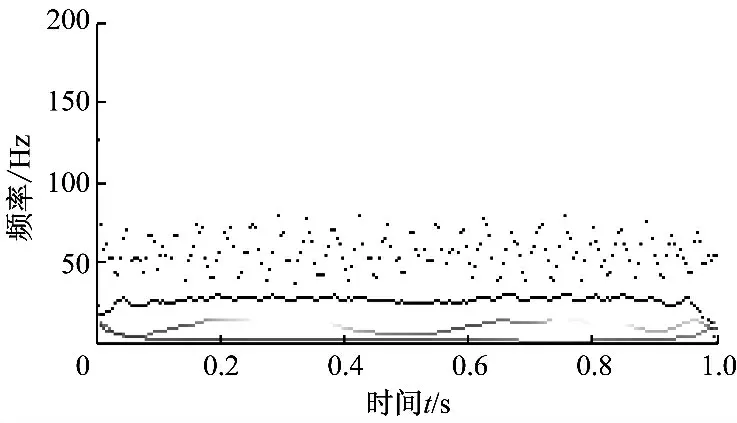
图12 油膜涡动信号的EMD方法时频图Fig.12 Time－frequency spectrum of oil whirl signals based on EMD

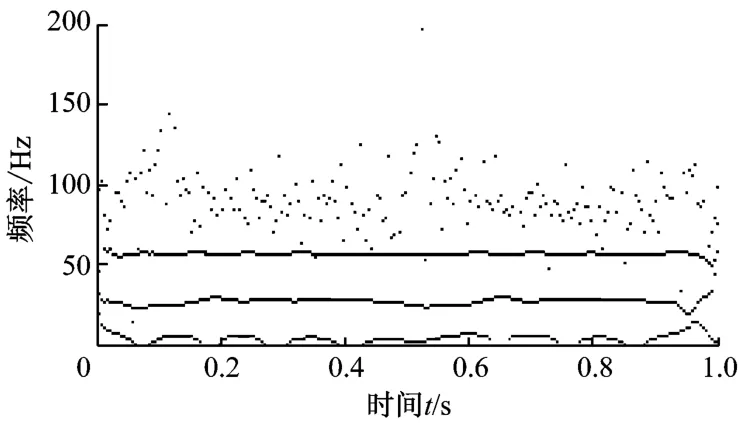
图13 油膜涡动信号的EWT 方法时频图Fig.13 Time－frequency spectrum of oil whirl signals based on EWT

3.3.2 油膜振荡

通过调节油泵、预紧力支架和调速电机控制器，使转子的转速达到6 500r／min，从而产生油膜振荡［15］.设置采样频率为1 280 Hz，通过数据采集设备，任意选取故障数据中的1 000个点，分析比较采集到的数据.

图14给出了6 500r／min油膜振荡信号的时域图、频域图和轴心轨迹.从图14可以看出，油膜振荡信号的时域波形为正弦信号的叠加，而在频谱图中出现了108Hz的基频分量和略低于二分频的频率为41Hz的油膜振荡故障频率，且故障频率幅值较基频幅值高；同时，转子的轴心轨迹杂乱无章，显然已经发生了油膜振荡.但是单纯从频谱图是无法判断故障是否发生的.

图14 油膜振荡信号的时域图、频域图和轴心轨迹Fig.14 Time wave form，spectral diagram and axis orbit of oil film vibration signals

图15 和图16分别为EMD 方法和EWT 方法对6 500r／min油膜振荡信号分析处理的结果.从图15和图16可以看出，故障频率为41 Hz，但是通过对比发现，EWT 方法还分解得到了信号的基频（108Hz）以及故障频率的二分频，且EWT方法时频图谱线比EMD 方法时频图谱线清晰，模态混叠现象明显减轻，且端点效应也得到一定的抑制，故障特征值明显，故障诊断效果显著.

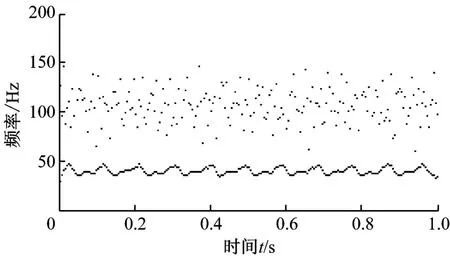
图15 油膜振荡信号的EMD方法时频图Fig.15 Time－frequency spectrum of oil film vibration signals based on EMD

图16 油膜振荡信号的EWT 方法时频图Fig.16 Time－frequency spectrum of oil film vibration signals based on EWT

4 结 论

本文提出了一种基于经验小波变换（EWT）的信号处理方法，针对仿真信号与转子系统实验故障信号对EWT 方法与EMD 方法的性能进行了比较研究.结果表明，EWT 方法分解得到的故障频率成分明显多于EMD 方法，且各频率成分清晰明确，调制现象和端点效应有所减弱，避免了模态混叠效应，提取的故障特征值明显，能够有效地分析机械故障信号.并且，EMD 方法分解得到的IMF分量总是明显多于信号本身所包含的分量，存在许多虚假分量，而EWT 方法分解得到的分量成分与信号所包含的分量成分数量一致，这在一定程度上减少了计算量，缩短了计算时间.该方法为旋转机械故障诊断提供了一种新的手段.

［1］ 张晔.信号时频分析及应用［M］.哈尔滨：哈尔滨工业大学，2006.

［2］ 向玲，唐贵基，胡爱军.旋转机械非平稳振动信号的时频分析比较［J］.振动与冲击，2010，29（2）：42－45.XIANG Ling，TANG Guiji，HU Aijun.Vibration signal＇s time－frequency analysis and comparison for a rotating machinery［J］.Journal of Vibration and Shock，2010，29（2）：42－45.

［3］ YEH Poliang，LIU Peiling.Application of the wavelet transform and the enhanced Fourier spectrum in the impact echo test［J］.NDT and E International，2008，41（5）：382－394.

［4］ 向玲，杨世锡，唐贵基，等.汽轮发电机组轴系扭振的时频特征分析［J］.动力工程学报，2011，31（9）：649－654.XIANG Ling，YANG Shixi，TANG Guiji，et al.Time－frequency analysis on torsional vibration of turbo－generator shafts［J］.Journal of Chinese Society of Power Engineering，2011，31（9）：649－654.

［5］ LOH C H，WU T C，HUANG N E.Application of the empirical mode decomposition－hilbert spectrum method to identify near－fault ground－motion characteristics and structural responses［J］.Bulletin of the Seismological Society of America，2001，91（5）：1339－1357.

［6］ 孟宗，顾海燕，李姗姗.基于神经网络集成的B样条经验模态分解端点效应抑制方法［J］.机械工程学报，2013，49（9）：106－112.MENG Zong，GU Haiyan，LI Shanshan.Restraining method for end effect of B－spline empirical mode decomposition based on neural network ensemble［J］.Journal of Mechanical Engineering，2013，49（9）：106－112.

［7］ GILLES J.Empirical wavelet transform［J］.IEEE Transactions on Signals Processing，2013，61（16）：3999－4010.

［8］ GILLES J.TRAN G，OSHER S.2D empirical transforms，wavelets，ridgelets and curvelets revisited［J］.SIAM Journal on Imagine Sciences，2014，7（1）：157－186.

［9］ 陈浩，郭军海，齐巍.基于经验小波变换的目标加速度估计算法［J］.北京航空航天大学学报，2015，41（1）：154－159.CHEN Hao，GUO Junhai，QI Wei.Estimation of target＇s acceleration based on empirical wavelet transform［J］.Journal of Beijing University of Aeronautics and Astronautics，2015，41（1）：154－159.

［10］ FRANCIS A，MURUGANANTHAM C.empirical wavelet transform and its application［J］.International Journal of Electrical，Electronics and Communication Engineering，2015，1（1）：1－3.

［11］ FRANCIS A，MURUGANANTHAM C.An adaptive denoising method using empirical wavelet transform［J］.International Journal of Computer Applications，2015，117（21）：18－20.

［12］ 熊慧英，何洁，严爱芳.烟气轮机转子不平衡故障诊断研究［J］.噪声与振动控制，2008（5）：86－90.XIONG Huiying，HE Jie，YAN Aifang.Imbalance fault diagnosis of gas turbine rotor［J］.Noise and Vibration Control，2008（5）：86－90.

［13］ 胡三高，安宏文，马志勇，等.基于小波奇异值分析的汽轮机碰磨特征提取［J］.动力工程学报，2013，33（3）：184－188.HU Sangao，AN Hongwen，MA Zhiyong，et al.Feature extraction of rubbing fault for steam turbines based on wavelet singularity analysis［J］.Journal of Chinese Society of Power Engineering，2013，33（3）：184－188.

［14］ 刘卜瑜.基于二次EEMD 的WVD 算法及在振动信号分析中的应用［D］.秦皇岛：燕山大学，2011.

［15］ 唐贵基，向玲，朱永利.基于HHT 的旋转机械油膜涡动和油膜振荡故障特征分析［J］.中国电机工程学报，2008，28（2）：77－81.TANG Guiji，XIANG Ling，ZHU Yongli.Fault analysis of oil whirl and oil whip based on Hilbert－Huang transform for rotor system［J］.Proceedings of the CSEE，2008，28（2）：77－81.