带副翼垂直轴风力机的一种控制策略

李润杰， 李 春，2， 杨 阳， 聂佳斌

（1.上海理工大学 能源与动力工程学院，上海200093；2.上海市动力工程多相流动与传热重点实验室，上海200093）

与水平轴风力机相比，垂直轴风力机可捕获来自任意方向的来流风，因此不需要复杂的偏航装置，结构设计简单，成本低［1］，且垂直轴风力机可地面安装，便于维修、检修和控制，其结构具有固有优势，适应环境能力强［2－3］.由于垂直轴风力机的结构特点，其建造高度较低，不仅不影响景观而且可抵御恶劣环境［4］，但目前，垂直轴风力机却没有像水平轴风力机那样大规模的商业化，主要原因是其难以自启动，难以控制失速（即易失速），加工工艺不成熟以及风能利用率低［5］.垂直轴风力机的流场特点有：典型的非定常性、非线性，存在强烈的干扰，风力机尾迹流场存在各种尺度的漩涡，旋转效应隔断了大涡向小涡的能量传递，使流动呈现大涡占主导的状态［6］.垂直轴风力机叶片运行时，绝大部分区域所受的空气动力都为正的驱动转矩，但在90°和270°附近时翼型的弦线与风向平行或接近平行时，气流相对速度较小，而阻力与升力的比值较大，产生负的驱动转矩，因此需要降低升力型垂直轴风力机的风能利用系数［7］.Xiao等［8］研究了固定副翼和摆动副翼对输出功率的影响.Reddy等［9］就半经验式的动态失速预测模型进行了综合论述，这些模型可以较大地改善总体气动载荷的预测效果，但无法反映动态失速现象的局部细节.Mehta［10］采用流函数－涡量表达式，使用有限差分法模拟了NACA0012翼型俯仰运动状态下的动态失速现象.Shida等［11］通过对N－S基本方程的数值求解，研究了雷诺数为6.85×105，马赫数为0.3时，NACA0012翼型俯仰运动状态下的可压绕流运动.Berezin等［12］结合循环控制技术，研究了椭圆翼型动态失速控制策略.

由于垂直轴风力机翼型处于不同方位角，因此所受到的升阻力不同.在风轮旋转的每个周期中，风轮主轴的输出力矩和风轮所受离心力随着时间变化，这是垂直轴风力机产生振动的根本原因，随着尖速比的增大，输出力矩变化频率提高［13］.长此以往，垂直轴风力机振动载荷会加剧其结构疲劳，从而影响风力机的使用寿命.而使用寿命是风力机性能衡量中的重要指标.由于风轮转矩脉动频率是与风力机旋转周期直接相关的，而给定尖速比、风速及风轮半径后，旋转周期是确定的，因此，为了降低主轴的疲劳载荷只能通过减小风力机运行时的振幅来实现，从而起到保护风力机的作用.

笔者根据以往研究的基础，提出了通过对副翼摆动施加反函数控制，以缩小风力机翼型在各个方位角上翼型升阻力系数的差距，从而减小振幅，改善风力机翼型周围流场和涡量的发展.

1 翼型选取及计算域划分

1.1 风力机翼型及几何参数

由于垂直轴风力机为对称结构，且重点研究旋转风轮流场的动态特性，故采用二维模型进行非定常计算，除叶尖与叶根部分，计算结果仍能较好地反映风力机气动特性［14－16］.根据WANXIANG 2号电站［17］所用40kW 垂直轴发电机，数值模拟所用垂直轴风力机模型参数选取如下：风轮半径为2m，叶片数目为3，叶片所用翼型弦长为0.2m［9］.其中，叶片所用翼型选取经典翼型NACA0012，其几何结构示意图如图1所示，其中C 为翼型弦长，D 为翼型最大厚度.

图1 NACA0012翼型几何结构示意图Fig.1 Structural diagram of the NACA0012airfoil

1.2 模型建立及计算域网格划分

图2 中，原始弦长表示原始NACA0012翼型的弦长C，而实际弦长C′是指摆角变化后的弦长，此间的夹角可以认为是对应攻角偏移量.

图2 翼型弦线变化示意图Fig.2 Chord changes of the airfoil

通过三角变换计算得到副翼摆角θ与攻角改变量α′的对应关系：

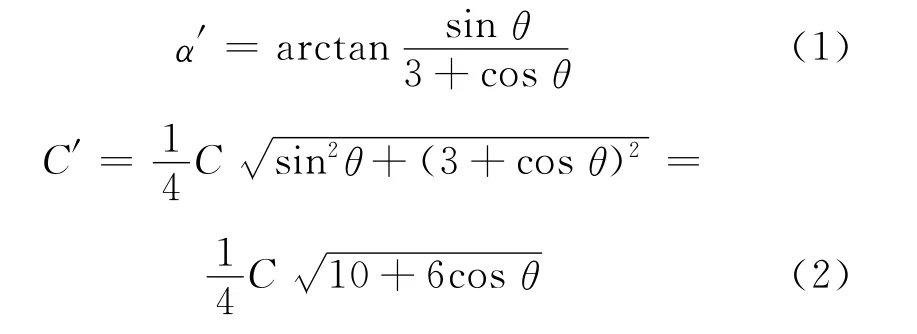
达里厄型垂直轴风力机风轮实际结构复杂，在CFD 模拟时需对其结构进行简化.由于要对风轮流场进行瞬态模拟，故采用二维计算比三维计算节省时间，并且计算结果仍能反映风力机的气动规律［18］.图3 为 简 化 后的二维几 何 模 型.其 中R3＝10R1，ae＝20R1.流体介质选用空气，密度ρ＝1.225 kg／m3，动力黏度μ＝1.789 4×10－5kg／（m·s）.给定来流速度，计算雷诺数Re＝6.85×105，马赫数Ma＝0.03.整体上下边界ae，cd 以及前端abc 设置为速度进口，后端边界egd 设置为压力出口，叶片部分设置为无滑移壁面，af、cf为不动的虚拟壁面设置为Interior，内流域Z1、主体旋转流域Z2以及外流域Z3的交界面设置成Interface.

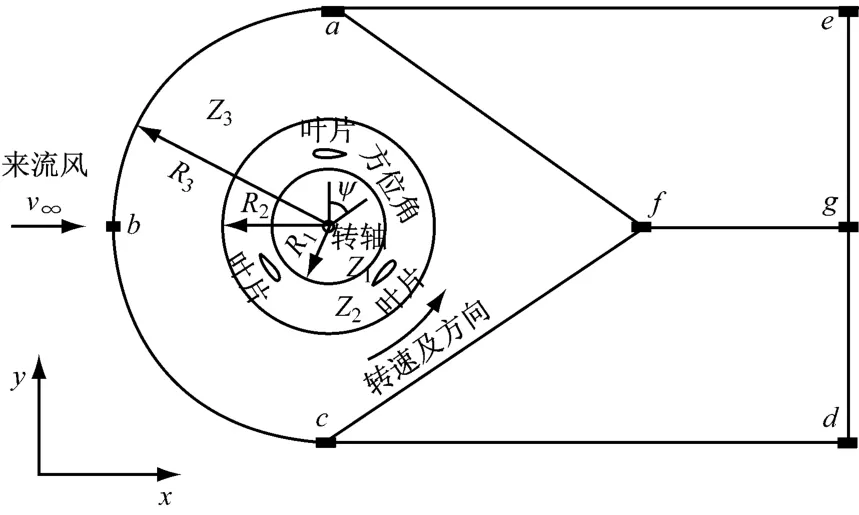
图3 垂直轴风力机二维简化示意图Fig.3 Simplified two－dimensional diagram of the vertical axis wind turbine

CFD 计算主要采用滑移网格技术描述旋转风轮.将计算域划分为3个域（图3中Z1、Z2和Z3流域）.对翼型表面区域网格进行局部加密（如图4（a）所示），近壁面网格（距翼型表面最近的一层网格）高度为0.000 1，叶片壁面处处于0.9～9.5之间，满足黏性流计算对壁面网格的要求.加密网格经网格无关性验证后，得到计算域的网格总数为532 142.翼型周围网格划分如图4（b）所示.

图4 流场整体及翼型周围网格划分Fig.4 Grid division of the whole flow field and the area around the airfoil

2 结果与分析

2.1 计算精度验证

为证明流场求解精度、网格生成质量、湍流模型的选取以及进出口边界条件的给定，分别将采用Fluent的CFD 计算值和Xfoil的计算值与文献［19］进行比较.

对于处于静态失速的翼型，其计算数据存在一定误差，CFD 的静态计算此时只能起到定性分析的作用.图5给出了Re＝7×105时，翼型升阻力系数的实验值、Xfoil计算值和CFD 计算值的比较.从图5可以看出，无论是CFD 计算值还是Xfoil计算值，失速前误差很小，不超过5%，但在失速后，包括实验值，都存在一定的计算误差，但是CFD 计算所得升、阻力系数的整体趋势与实验值吻合度较高，较好地证明了本文所用方法的有效性.

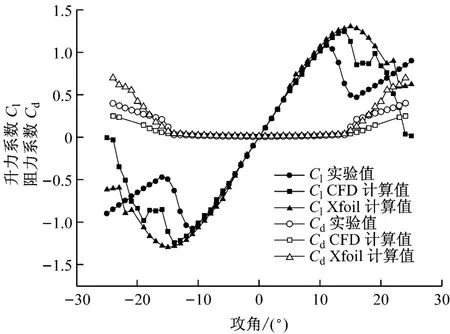
图5 Xfoil计算、CFD计算及实验所得升、阻力系数的对比Fig.5 Comparison of lift／drag coefficient among Xfoil calculation，CFD calculation and experimental results

2.2 垂直轴风力机的气动性能

垂直轴风力机运行时，叶片转子周围的流场显示出非常强的非定常性，在叶片转子尾部区域，既有外部流场流经翼型时形成的大尺度涡，也有单个翼型近壁面形成的小尺度涡，在每个翼型的尾迹区域，处于不同的方位角时，会形成不同程度的涡.由于垂直轴风力机的运转特性，叶片旋转时，必然经过大攻角位置，而在大攻角下，翼型失速明显，动态失速的明显特征表现为翼型周围涡脱落.图6给出了翼型周围涡的形成发展过程.从图6可以看出，垂直轴风力机风轮旋转过程中，翼型尾涡逐渐在翼型尾部脱落.翼型方位角较小时，翼型周围流场较稳定，无较大涡脱落，而翼型所处方位角较大时，翼型尾涡脱落较明显.翼型前缘的来流不仅受到外部流场的影响，同时也受上风区翼型尾涡的影响，且上风区翼型尾涡和风力机固定轴周围流场对下风区翼型周围涡的发展有较大影响.

图6 翼型周围涡的形成发展过程Fig.6 Formation and development of vortex around the airfoil

2.3 添加控制策略的垂直轴风力机气动性能的改善

为了更好地改善翼型周围涡的发展，根据风力机叶片方位角与攻角之间的关系，提出减振控制思想，在不同方位角下求出相应副翼摆角，控制方程为

将θ＝ωt代入式（3）并对时间t求导：

式中：k1为副翼摆角最大控制因子；λ 为尖速比；ω为叶片旋转角速度.

控制因子k1用于设定副翼摆角的最大幅值.如k1＝±20°，则副翼摆角幅值可达±20°.对于副翼摆角的范围，考虑到摆角增大后阻力将提高，并非摆角越大减振效果越好，过大的摆角甚至会影响风力机整体的做功性能.因k1与方位角ψ 是反函数的关系，故称此种控制策略为反函数控制策略.

静态特性下，反函数控制策略下的攻角变化如图7所示.从图7可以看出，添加副翼控制后，翼型旋转过程中翼型攻角均不超过静态临界失速攻角，其中α和k1是由计算其反函数得出.

图7 叶片静态时反函数控制策略下的攻角变化规律Fig.7 Variation of attack angle with inverse function control strategy in static state of blade

图8 为反函数控制策略下翼型周围尾涡的分布情况，图中左列为无副翼控制策略时的翼型尾涡分布，右列为添加反函数控制策略后的翼型尾涡分布.从翼型周围的尾涡分布能够明显观察到尾涡结构的变化，在添加了反函数控制策略之后，翼型能够完全处在静态失速范围内运行，此时翼型尾缘大分离涡消失，气动性能得到较好的改善.当风轮旋转过程中，叶片方位角处于180°＜Ψ＜270°时容易发生失速分离，使得尾缘发生回流，产生大尺度涡，在此范围内翼型的阻力系数也是整个运行周期中最高的区域.从尾涡结构的变化能够看出，这种反函数控制策略不仅能够改变幅值变化的大小，甚至在一定程度上抑制了失速涡的脱落，改善了风力机气动性能，促进其旋转.

图8 反函数控制策略下翼型周围尾涡分布Fig.8 Vortex distribution around the airfoil with inverse function control strategy

图9 为无副翼控制策略和反函数控制策略时整个流场的涡量分布情况.从图9可以看出，有无控制策略的流场中，最大的区别是翼型周围圆形尾缘涡的分离情况，对于无副翼控制策略的情况，叶片在180°＜Ψ＜270°范围内圆形尾涡脱落明显，当添加反函数控制策略后，尾涡顺着风轮旋转的方向发展，其脱落的情况大为改善，可见反函数控制策略起到了改变翼型尾涡结构的作用，使涡量值减小，流场耗散减小，提高了风能利用率.反函数控制策略的最大效用主要体现在风力机整体转矩的变化上，即添加反函数控制策略的流场将明显观察到转矩系数幅值的减小，其曲线特征明显改变，所对应的涡量分布图较未添加控制策略的涡量分布图更均匀（见图9（b））.

图9 有无反函数控制策略时的流场涡量分布Fig.9 Vorticity distribution with and without inverse function control strategy

由于转矩系数是计算整个风力机做功性能的重要参数之一，且能够真实反映主轴受到的瞬态力矩大小，对于受力或结构分析具有一定意义.图10给出了反函数控制策略下转矩系数曲线图.从图10可以看出，带有反函数控制策略的转矩系数曲线振幅较无副翼控制策略原始曲线减小50%，其物理意义为：对于垂直轴风力机，每个旋转周期上受到的最大转矩均减小约50%，从而延长风力机运行寿命；虽然转矩系数曲线的振幅明显降低，但曲线平均值并没有降低，这表示添加反函数控制策略并不会降低风力机输出功率，因此反函数控制策略并不是以降低出力为代价来控制振幅的.

图10 反函数控制策略下转矩系数曲线Fig.10 Curves of torque coefficient with inverse function control strategy

添加反函数控制策略的副翼摆角幅度的大小会影响风力机平均转矩系数的输出.随着摆角的增大，转矩输出并不是一味的提升，而是一个先增后减的趋势.同时，减幅控制策略的引入对提高整体扭矩的效果微小，几乎能够忽略不计，若考虑计算误差或真实情况下的机构影响，这种提高效果并不能起到抬升扭矩的作用.

3 结 论

（1）在所处方位角范围内，反函数控制策略使垂直轴风力机在运行过程中的叶片所用翼型均在静态失速的控制范围内.

（2）反函数控制策略改善了翼型的尾迹涡，翼型周围没有发生大分离流动，整个流场区域对应的涡量分布图较未添加反函数控制策略的涡量分布图更均匀，改善了垂直轴风力机的气动性能.

（3）反函数控制策略的主要目标是降低垂直轴风力机旋转周期中的转矩系数幅值，其降低了风轮的疲劳强度，在没有减小风力机出力的前提下，增加了风力机的运行时间.

［1］ HOWELL R，QIN N，EDWARDS J，et al.Wind tunnel and numerical study of a small vertical axis wind turbine［J］.Renewable Energy，2010，35（2）：412－413.

［2］ ISLAM M，DAVID S，TING K，et al.Aerodynamic models for Darrieus－type straidht－bladed vertical axis wind turbines［J］.Renewable and Sustainable Energy Reviews，2008，12（4）：1087－1109.

［3］ POPE K，DINCER I，NATERER G F.Energy and exergy efficiency comparison of horizontal and vertical axis wind turbines［J］.Renewable Energy，2010，35（9）：2102－2103.

［4］ ERIKSSON S，BERNHOFF H，LEIJON M.Evaluation of different turbine concepts for wind power［J］.Renewable ＆Sustainable Energy Reviews，2008，12（5）：1419－1434.

［5］ 吴双群，赵丹平.风力发电原理［M］.北京：北京大学出版社，2011：33－34.

［6］ 芮晓明，马志勇，康传明.并网型垂直轴风力机的基本构成与气动特性［J］.太阳能，2007（2）：28－31.RUI Xiaoming，MA Zhiyong，KANG Chuanming.Basic structure of grid type vertical axis wind turbines and aerodynamic characteristics［J］.Solar Energy，2007（2）：28－31.

［7］ 赵振宇.风力机原理与应用［M］.北京：中国水利水电出版社，2011：10－20.

［8］ XIAO Q，LIU W，INCECIK A.Flow control for VATT by fixed and oscillating flap［J］.Renewable Energy，2013，38（51）：141－152.

［9］ REDDY T S R，KAZA K R V.A comparative study of some dynamic－stall models［R］.USA：NASA Tech Memo 88917，1987.

［10］ MEHTA U.Dynamic stall of an oscillating airfoil［C］／／Proceedings AGARD CP－227，Symposium on Unsteady Aerodynamics.USA：［s.n.］，1977.

［11］ SHIDA Y，KUWAHARA K.Computation of dynamic stall of a NACA－0012airfoil［J］.AIAA Journal，1987，25（3）：408－413.

［12］ BEREZIN C，SANKAR L.Improvements to a tightly coupled viscous－inviscid procedure for three－dimensional unsteady transonic flow［J］.Computer and Fluids，1998，27（5／6）：689－694.

［13］ ION Paraschivoiu.垂直轴风力机原理与设计［M］.李春，叶舟，高伟，等，译.上海：上海科学技术出版社，2013：85－118.

［14］ 徐璋，王茜，皇甫凯林，等.襟翼对垂直轴风力机性能影响的数值模拟［J］.动力工程学报，2011，31（9）：715－719.XU Zhang，WANG Qian，HUANGFU Kailin，et al.Influence of various flaps on performance of vertical axis wind turbines［J］.Journal of Chinese Society of Power Engineering，2011，31（9）：715－719.

［15］ 杨从新，巫发明，张玉良.基于滑移网格的垂直轴风力机非定常数值模拟［J］.农业机械学报，2009，40（6）：98－102.YANG Congxin，WU Faming，ZHANG Yuliang.Numerical simulation on unsteady rotated flow of a vertical axis wind turbine based on moving meshes［J］.Transactions of the Chinese Society of for Agricultural Machinery，2009，40（6）：98－102.

［16］ ALMOHAMMADI K，INGHAM D，MA L，et al.CFD sensitivity analysis of a straight－blade vertical axis wind turbine［J］.Wind Engineering，2012，36（5）：571－588.

［17］ CASTELLI M R，ENGLARO A，BENINI E.The Darrieus wind turbine：proposal for a new performance prediction model based on CFD［J］.Energy，2011，36（8）：4919－4930.

［18］ 廖书学，李春，聂佳斌，等.不同翼型对垂直轴风力机性能的 影 响［J］.机 械 设 计 研 究，2011，27（3）：108－111.LIAO Shuxue，LI Chun，NIE Jiabin，et al.The analysis of aerodynamic performance for small H type VAWT based on different airfoils［J］.Mechanical Design and Research，2011，27（3）：108－111.

［19］ SVORCAN J，TUPAR S，KOMAROV D，et al.Aerodynamic design and analysis of a small－scale vertical axis wind turbine［J］.Journal of Mechanical Science and Technology，2013，27（8）：2367－2373.