基于改进DE算法的PID 参数整定及其应用

王 朋， 刘 林， 陈 哲， 翟永杰， 周杰联

（1.广东电网有限责任公司电力科学研究院，广州510080；2.广东电网有限责任公司佛山供电局，广东佛山528000；3.华北电力大学 河北省发电过程仿真与优化控制重点实验室，河北保定071003）

近年来，随着人工智能的发展，许多新型智能控制算法在理论上已被证明优于传统的PID 控制算法.然而，在实际的工业过程中，特别是在热工控制领域中，占主导地位的控制策略仍是PID 控制.PID控制器的控制效果取决于控制器参数的取值，控制器参数的整定一直是一个重要的研究课题.传统的试凑法需要运行人员的经验，而且精度不高.近年来，许多学者引入了一些智能寻优算法，如蚁群算法（ACO）［1］、遗传算法（GA）和粒子群优化（PSO）［2］算法等，这些算法虽然提高了优化精度，但自身较为复杂，易陷入局部最优.

微分进化（DE）算法从GA 发展而来，是一种高效智能且无需编码和解码的优化算法，具有速度快、鲁棒性强和在实数域上搜索能力强的优点，被认为是一种极具潜力的跨学科优化算法，其在解决优化问 题中具有 比GA 和PSO 算 法 更 明 显 的 优 势［3－6］.笔者在DE算法的基础上，为提高搜索效率和速率，引入经验整定公式和自适应算子，提出了改进的微分进化（IDE）算法，即基于经验整定公式的参数自适应的DE 算法，并将其应用于某循环流化床（CFB）锅炉主汽温控制系统的PID 参数整定.

1 DE算法

DE算法基于种群进化，对当前种群进行变异、交叉和选择后产生新一代种群，并使种群逐步达到接近最优解的状态，是一种基于实数编码的贪婪GA［7］.假设需要优化的参数为x1，x2，…，xm，共m个，则DE算法可表示为求解如下优化问题：

式中：ai和bi分别为xi的下限和上限，｛（ai，bi）｝构成了m 维优化参数定义空间S0，表征了DE 算法的寻优范围.

假设在DE算法中每一代G 中有NP个个体，即种群规模为NP.设G 为当前进化代数，则第G 代可表示为，其中为第G 代的第i个个体.DE算法的具体步骤如下：

（1）变异操作.生成变异个体的方法为

（2）杂交操作.DE 算法利用杂交操作以保持种群的多样性，其实现过程如下：将变异生成的个体和当前的个体进行二项分布杂交操作，生成杂交个体uG＋1i，即

式中：k（i）为｛1，2，…，m｝内的随机参数；rand（j）为均匀分布的随机数，rand（j）∈［0，1］；CR为杂交因子，CR∈［0，1］，通过控制选择变异的个体分量来替代当前点分量值的概率.

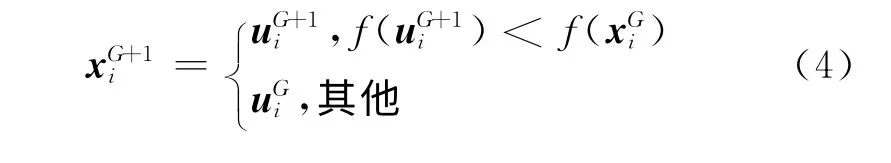
2 基于经验整定公式的参数自适应DE算法

2.1 经验整定公式

DE算法最优解的优劣取决于初始集合是否能够包含解空间的全部可能解集，并在遗传进化过程中不失去其优良的特性［7］.需要通过增加搜索力度使初始种群尽量散布在最有希望获得最优解的解空间区域.因此，DE算法初始种群的产生方式会大大影响其应用效果.DE 算法初始种群通常通过对各控制变量的取值范围内取随机数来获得.

由于本文研究的DE 算法用于PID 参数的优化，其初始种群的确定实质上是PID 参数范围的确定.目前，大多数研究均采用经验试凑法来求取PID参数的初始范围，这种方法对工程技术人员的经验要求较高，而且很难找到最优的参数结果.Zhang等［1］经过大量实验得出了一组求取PID 参数的经验整定公式，并验证了这些公式的有效性，利用该方法计算得到的PID 参数即可确定其大致范围.

热工对象一般分为有自平衡对象和无自平衡对象，其数学模型的描述形式分别为：

式中：K 为对象静态增益；e－τs为纯迟延环节；τ为纯迟延时间；T 为过程的惯性时间常数；n 为对象的阶次.

Bailey PID 控制器的传递函数［8］为

式中：δ 为比例带，等于比例增益Kp的倒数；Ti为积分时间；Td为微分时间.

所研究的CFB 锅炉主汽温控制系统是典型的有自平衡对象，因此只给出了有自平衡对象的PID参数经验整定公式［9］：

通过计算可直接得到PID 参数，利用该方法可以指导DE算法的寻优范围：即先采用经验整定公式计算出PID 参数，得到DE算法的寻优范围，再利用DE算法在此范围内对参数进行微调，搜索最佳参数值，有效地提高了优化的精度和收敛速度.

2.2 参数自适应算子

DE算法的性能除与寻优范围有关外，还与自身的参数有很大关系，如变异率F 和杂交因子.F 越大，种群中个体的振荡幅度就越大，有利于其变量的多样性，但收敛速度变慢；F 取值小则可以提高算法的收敛速度，但易陷于局部最优点.因此，在计算初期为获得多样性的变量，F 应取较大值，而在计算末期为了提高收敛速度，F 应取较小值.CR取值过小会导致种群在杂交操作后产生的新个体变少，降低了算法拓展新空间的能力；CR取值过大不利于种群的稳定性，进而降低了算法的稳定性.因此，CR在计算初期应取较大值、计算末期取较小值.借鉴PSO 算法中惯性权重的思想，引入自适应算子，F 和CR随进化代数进行自适应调整，即

式中：Gmax为最大进化代数；Fmin和Fmax分别为最小和最大变异率；Cmin和Cmax分别为最小和最大杂交因子.

由式（11）和式（12）可知，F 和CR在初始阶段较大，全局搜索能力较强，F 和CR均随着进化代数的增大逐渐减小；F 和CR在后阶段均较小，局部搜索能力较强，既保证了全局搜索能力，又提高了收敛速度.

2.3 IDE算法优化PID 参数

在热工控制系统设计中，常采用绝对误差的二阶矩积分作为目标函数：

式中：Q 为目标函数；e（t）为第t时刻被调量与目标函数值的差值.

基于经验整定公式的自适应DE 算法优化PID参数的步骤如下：

（1）根据上文的PID 经验整定公式计算得到初始PID 参数：KP0、Ti0和Td0，从而确定DE算法的初始种群，即寻优范围；

（2）初始化IDE 参数，如NP＝40，Gmax＝500，Fmin＝0.4，Fmax＝0.9，Cmin＝0.3，Cmax＝0.9，产生初始种群，当前进化代数G＝1；

（3）对初始种群进行评价，按照式（13）计算目标函数值；

（4）判断是否满足结束条件，若是则输出最佳PID 参数组合.其中结束条件为：G＝Gmax＝500 或者适应度值小于1×10－4；

（5）对所有个体进行变异和杂交操作，得到临时种群，对临时种群进行评价，计算目标函数值，进行选择操作，得到新种群；

（6）更新G，即G ＝G＋1，然后转向步骤（4）.

3 IDE 算法优化CFB 锅炉汽温控制系统PID参数

3.1 数学模型分析

某CFB锅炉汽温控制系统采用串级调节方式，控制结构如图1所示，其中内环和外环均采用负反馈，θ1和θ2分别代表主汽温和导前区汽温，主副回路均采用PI调节器.

图1 汽温控制系统图Fig.1 Schematic diagram of the steam temperature control system

该系统的传递函数［11］为

式中：W1（s）为惰性区传递函数；W2（s）为导前区传递函数；当锅炉负荷在25%～100%内变化时，对应的K1为0.8～0.5，T1为100～80s，K2为2～1，T2为50～35s.

由此可以看出，随着锅炉负荷的增大，汽温控制系统的增益和惯性时间常数均相应地逐渐减小，同时表现出明显的大惯性特性，因此常采用上述串级双回路PID 控制方案.

3.2 控制器参数整定结果及性能分析

3.2.1 设定值跟踪实验

采用文献［10］中给出的经验公式，经整定计算得到初始PID 参数，即副调节器：δ01＝0.9，Ti01＝51.05s；主调节器：δ02＝0.9，Ti02＝180s.因此，可设定DE 算法的初始种群，即寻优范围：δ1＝［0.009，9］，Ti1＝［5.75，575］s，δ2＝［0.009，9］，Ti2＝［20，2 000］s.利 用IDE 算 法 寻 得 最 优PID 参 数：δ1＝0.998 8，Ti1＝228.057 7s，δ2＝0.062 2，Ti2＝359.124 2s.100%负荷下系统在设定值单位阶跃扰动时的仿真结果见图2，其中调节时间为762×（1±5%）s，超调量为1.747 3%.

图2 100%负荷下设定值单位阶跃扰动时系统的响应曲线Fig.2 System response to unit step disturbance of setpoint at 100%load

同时，图2给出了用GA 优化PID 参数的控制效果（图中实线），对应最优PID 参数为副调节器：δ01＝2.168 8，Ti01＝114.987 6s；主调节器：δ02＝0.091 8，Ti02＝17.389 9s.此时调节时间为1 094s（过程值与目标函数值偏差在±5%），超调量为8.133 1%.由图2中设定值单位阶跃扰动时系统的响应曲线可知，IDE算法相比于GA 具有较小的超调量和较短的调节时间，其控制效果和品质均优于GA.

3.2.2 鲁棒性实验

CFB锅炉汽温的惯性时间常数易受到负荷等因素的影响而发生变化，而对象静态增益也可能因为某种原因而变化.因此，根据可能的变化采用不同的传递函数进行仿真.

（1）假设对象的惯性时间常数由80s变为100 s，其传递函数为，相应的设定值单位阶跃扰动时系统的响应曲线如图3所示.

图3 惯性时间常数变化后系统的阶跃响应曲线Fig.3 System response to variation of inertia time constant

图4 对象静态增益发生变化后系统的阶跃响应曲线Fig.4 System response to variation of static gains

由图3和图4可知，当对象特性发生变化时，与GA 相比，通过IDE 算法整定得出的最优参数能够获得更好的控制效果，表明IDE 算法的鲁棒性较强，具有良好的调节品质.

3.2.3 减温水内扰实验

CFB锅炉中减温水流量的波动对主汽温的影响较大，在满负荷时对减温水流量进行单位阶跃扰动，相应的系统响应曲线如图5所示.由图5可知，通过IDE算法整定的PID 控制器对扰动具有较好的抑制作用，比经典的GA 整定后的控制效果好.

图5 减温水流量单位阶跃扰动时系统的响应曲线Fig.5 System response to unit step disturbance of attemperating water flow

3.2.4 实际应用效果

将IDE算法应用于某300 MW CFB 锅炉主汽温控制系统中，该串级控制回路是在ABB Symphony系统中组态实现的，并采用了变参数调节方案（见图6）.优化前的控制器参数采用文献［9］中的半经验整定法，对该锅炉负荷为50%、75%和100%时分别进行控制器参数整定，并采用折线函数实现调节器变参数的方法.稳定负荷时，控制回路的主汽温波动在10K 左右.采用IDE 算法分别进行了相应负荷下控制器参数的优化、调整，无论是变负荷还是稳定负荷，汽温控制效果均有明显改善，温度的控制误差小于5K（见图7），满足相关标准要求.

图6 某300 MW CFB锅炉主汽温控制系统Fig.6 Main steam temperature control system of a 300 MW CFB boiler

图7 某300 MW CFB锅炉主汽温控制系统优化前后的效果对比Fig.7 Comparison of main steam temperature control effect for the 300 MW CFB boiler before and after optimization

4 结 论

针对PID 参数的整定问题，引入DE 算法优化PID 参数，在此基础上采用自适应微分进化算法，提高了算法的收敛速度，避免了算法陷入局部收敛.利用PID 经验整定公式计算的结果指导初始种群数量，减少了不可行解的数目，加快收敛速度，避免了DE 算法寻优的随机性，且不需依赖调试人员的经验，实现完全自适应获得最优PID 参数.某CFB 锅炉汽温控制系统的仿真结果表明，利用IDE 算法来整定PID 控制器参数，其调节时间短、超调量小，获得了比经典GA 优化PID 控制器更好的效果；当对象特性和减温水流量发生变化时，同样能获得良好的控制效果，鲁棒性较强.将该算法应用于某300 MW CFB锅炉主汽温控制系统中，其汽温控制效果得到明显改善.

［1］ ZHANG Qian，DONG Ze，HAN Pu，et al.Optimization of controllers in the thermal system using initial pheromone distribution in ant colony optimization［C］／／IEEE International Conference on Information Reuse and Integration.Las Vegas，USA：s.n.，2008：22－27.

［2］ 谢谢，曾德良，刘吉臻，等.基于遗传算法的协调控制系统鲁棒PID 参数寻优化［J］.动力工程学报，2010，30（12）：937－940，959.XIE Xie，ZENG Deliang，LIU Jizhen，et al.Optimization of robust PID controllers for a coordinated control system based on genetic algorithm［J］.Journal of Chinese Society of Power Engineering，2010，30（12）：937－940，959.

［3］ 杨勇，王东风，焦嵩鸣.基于混沌PSO 的循环流化床汽温系统分数阶控制［J］.华北电力大学学报：自然科学版，2011，38（4）：12－16.YANG Yong，WANG Dongfeng，JIAO Songming.Design of fractional order control for steam temperature system of circulating fluidized bed boiler based on chaos particle swarm optimization method［J］.Journal of North China Electric Power University：Natural Science Edition，2011，38（4）：12－16.

［4］ 袁沔齐，邹振宇，孙凯祺，等.基于遗传算法和微分进化算法的分布式电源优化配置［J］.中国电力，2013，46（1）：4－7.YUAN Mianqi，ZOU Zhenyu，SUN Kaiqi，et al.Optimal allocation of distributed generation based on genetic algorithms and differential evolution algorithm［J］.Electric Power，2013，46（1）：4－7.

［5］ 王文兰，王巍，崔艳艳.改进PSO 算法优化超临界机组主汽温参数的研究［J］.广东电力，2013，26（10）：13－18.WANG Wenlan，WANG Wei，CUI Yanyan.Study on application of supercritical main steam temperature parameters based on improved particle swarm optimization algorithm［J］.Guangdong Electric Power，2013，26（10）：13－18.

［6］ 李岩，王东风，焦嵩鸣，等.采用微分进化算法和径向基函数神经网络的热工过程模型辨识［J］.中国电机工程学报，2010，30（8）：110－116.LI Yan，WANG Dongfeng，JIAO Songming，et al.Thermal process identification using differential evolution algorithm and radial basis function neural network［J］.Proceedings of the CSEE，2010，30（8）：110－116.

［7］ 张炳才，秦四娟，乔世军，等.基于改进微分进化算法的电力系统无功优化［J］.电力系统保护与控制，2010，38（15）：91－94.ZHANG Bingcai，QIN Sijuan，QIAO Shijun，et al.Reactive power optimization in power system based on modified differential evolution algorithm［J］.Power System Protection and Control，2010，38（15）：91－94.

［8］ DWYER O A.Handbook of PI and PID controller tuning rules［M］.2nd ed.Singapore：Imperial College Press，2006.

［9］ 韩璞，吕玲，张倩，等.基于经验整定公式的热工系统控制器参数智能优化［J］.华北电力大学学报：自然科学版，2010，37（5）：73－77.HAN Pu，LÜLing，ZHANG Qian，et al.Controller parameter intelligent optimization in thermal system utilizing regulation－based formulas［J］.Journal of North China Electric Power University：Natural Science Edition，2010，37（5）：73－77.

［10］ 薛晓强.基于改进微分进化算法的配电网分布式电源优化规划［D］.北京：华北电力大学，2009.

［11］ 王子杰，黄宇，韩璞，等.循环流化床锅炉汽温自抗扰控制器的优化设计［J］.动力工程学报，2010，30（1）：32－35.WANG Zijie，HUANG Yu，HAN Pu，et al.Optimal design of active disturbance rejection controller for steam temperature of circulating fluidized bed boilers［J］.Journal of Chinese Society of Power Engineering，2010，30（1）：32－35.