一类数列极限的几种常用方法

李啸芳，刘家保，左学武

（安徽新华学院公共课教学部，安徽合肥230088）

一类数列极限的几种常用方法

李啸芳，刘家保，左学武

（安徽新华学院公共课教学部，安徽合肥230088）

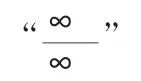
数列极限；归结原则；Stolz定理

1 对于三类通项有特点的数列极限的求法

1.1 有理分式的数列极限的求法

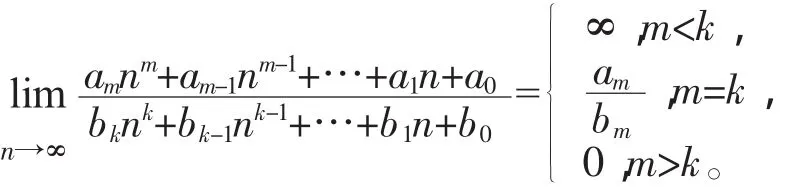
1.2 含根式的数列极限的求法

对于此类通项，常将分子分母同乘以其共轭，经过整理得出0为极限的因子。

1.3 含指数分式的数列极限的求法

2 利用其他有效的法则和方法求数列极限

2.1 利用归结原则、洛必达法则、等价无穷小替换、微分中值定理等

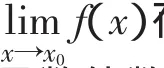
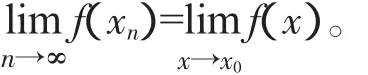
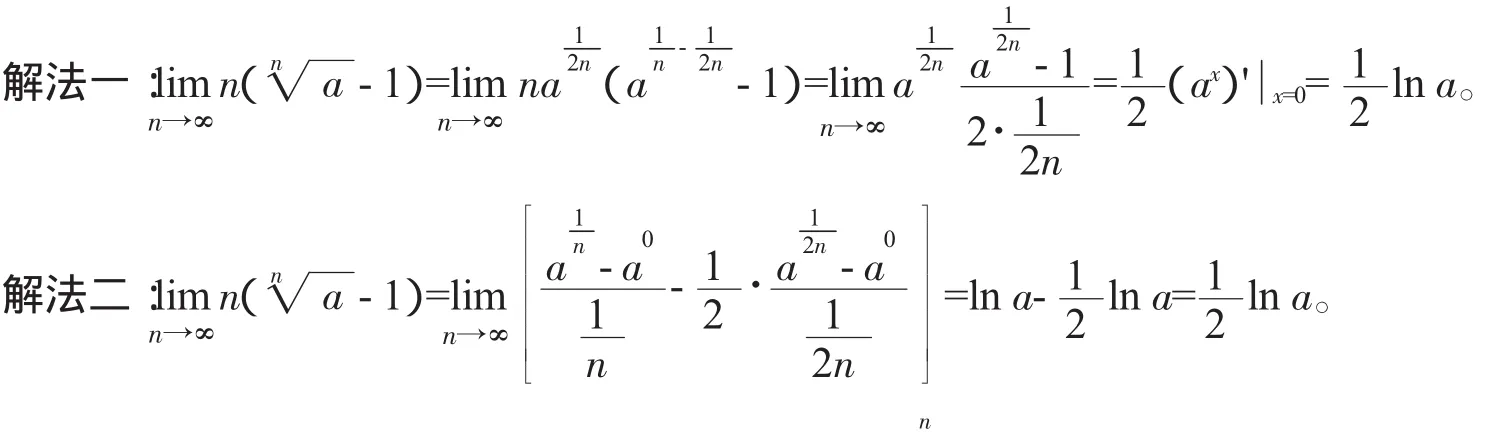
解由题设可知f（x）在a点的某个领域内大于零，故有

解Langrage中值定理［1-5］：若f（x）满足在［a，b］上连续，在（a，b）内可导，则至少存在一点ξ∈（a，b）使得f（b）-f（a）＝f'（ξ）（b-a）成立。

注该方法仅适用在满足归结原则的情况下，可以用函数极限求数列极限，因为函数是连续的，而数列是离散的，函数极限可以用洛必达法则、等价无穷小替换等方法求解。

2.2 利用级数

注此类方法仅适用于极限值为零的情形.

（2）构造幂级数。

2.3 利用迫敛法则

迫敛法则［2，4，7］：若

注该方法往往要根据通项的具体特点进行恒等变形及不等式的放大与缩小，需要较高的技巧。

2.4 利用定积分的定义

解由于

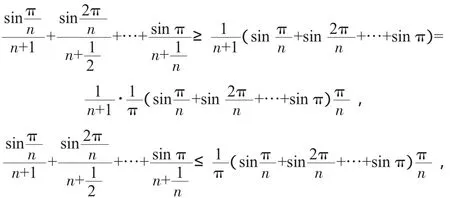
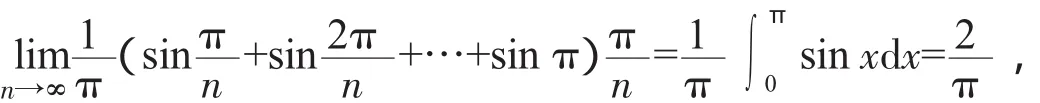
2.5 利用Stolz定理

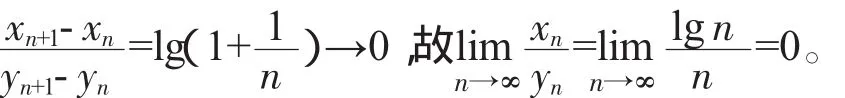
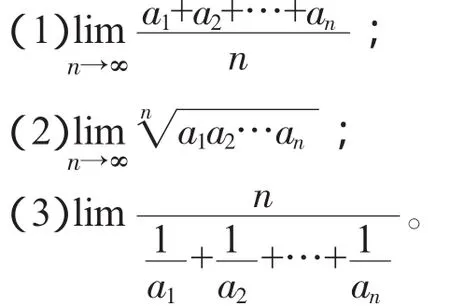
解（1）由Stolz定理立得。

注对一个各项为正且收敛于一个正数的数列，其算术平均、几何平均、调和平均都收敛于数列本身的极限。

2.6 由Stolz定理推出的定理

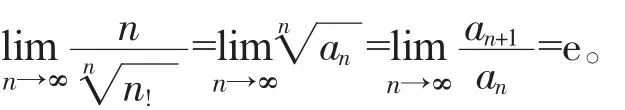
注该方法在一定程度上弥补了利用级数收敛的必要条件求数列极限的不足，但是仅仅解决类型为开n次根号的数列求极限。

［1］魏立明.一类数列极限求法的研究［J］.广西梧州师范高等专科学校学报,2004,20（4）∶75-77.

［2］同济大学数学系.高等数学［M］.6版.北京∶高等教育出版社,2007.

［3］费定晖,周学圣.数学分析习题集题解［M］.4版.山东∶山东科学技术出版社,2012.

［4］刘三阳,李广民.数学分析选讲［M］.北京∶科学出版社,2011.

［5］葛喜芳.数列极限的几种计算方法［J］.北京工业职业技术学院学报,2013,12（3）∶63-65.

［6］周林.高等数学中数列极限的几种求法［J］.湖北广播电视大学学报,2008,28（11）∶159-160.

［7］淮乃存.利用定积分定义求数列极限［J］.陕西师范大学学报∶自然科学版,2003,31（S1）∶30-33.

【责任编辑：王桂珍foshanwgzh@163.com】

Several commonmethodsof a classof sequence lim it

LIXiao-fang，LIU Jia-bao，ZUOXue-wu

（DepartmentofCommom Course,AnhuiXinhua University,Hefei230088,China）

sequence limit;ending principle;Stolz theorem

O171

A

1008-0171（2015）01-0014-05

2014-04-16

安徽省高等学校省级自然科学基金项目（KJ2013B105.）；安徽新华学院质量工程项目（2012jy045,2012jgkcx03, 2013jgkcx09）；国家级大学生创新创业训练计划项目（201312216030，201312216032）

李啸芳（1988-），女，安徽合肥人，安徽新华学院助教。