高层建筑主动变刚度多模态抗震分析
2015-06-05张月香
张 月 香
(上海同建强华建筑设计有限公司,上海 200092)
高层建筑主动变刚度多模态抗震分析
张 月 香
(上海同建强华建筑设计有限公司,上海 200092)
提出了一种基于动能为性能控制指标的AVS系统的控制算法——多模态法,通过数值仿真分析研究了该方法应用于高层建筑抗震设计的控制效果,结果表明:多模态法具有计算精度高和计算速度快的优点,解决了主动变刚度控制中的在线控制问题。
高层建筑,抗震设计,多模态
0 引言
结构抗震设计主要致力于保证结构自身具有一定的强度、刚度和延性,以满足一定的抗震要求。在这种设计中,结构处于被动抵御地震的地位,因此是一种消极的设计[1]。AVS控制系统的工作过程是:选定控制时间步长,在每一步长内:首先,观测地震动信息,将观测到的信息传递给计算机;然后,根据预先设置的控制算法预测出下一步的地震动趋势,并选择出最佳的结构刚度避开地震频率,建立所谓的反共振状态,使下一步的结构响应最小;最后,计算机向VSD传递控制信息,VSD据此改变结构的刚度,使之为上一步中确定的刚度。
该文提出了基于动能为性能控制指标的AVS系统的多模态法控制算法,并进一步比较了多模态法与枚举法的控制效果和控制效率。
1 力学模型与运动方程
从线性振动理论可知,系统或结构的振动可以将它置于模态空间来考虑,多自由度系统在时间域内的振动通常可以用其低阶自由度模态的组合来近似地加以描述,这样,多自由度系统的振动控制可转化为在模态空间内少量几个模态的振动控制,亦即控制模态,这种方法成为模态控制法,其中分为模态耦合控制法和独立模态空间控制法两种,后者可实现对所需控制的模态进行独立的控制,不影响其他未控的模态,具有易设计的优点[2]。该文提出的多模态控制法的依据是独立模态空间控制法,在误差允许的条件下,忽略次要因素,对结构的运动方程解耦,以实现对模态的独立控制。
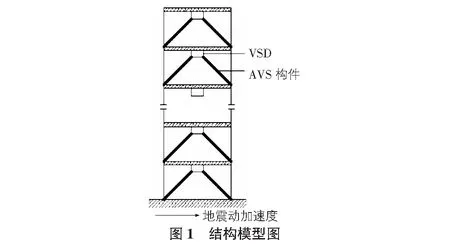
考虑一幢如图1所示的n层剪切型结构,在其中的m层布置了AVS构件,对其进行AVS控制,结构的运动方程如式(1)所示,即:
(1)
[K(t)]=[K0]+[Kc(t)],其中[K0]为原结构(不考虑AVS系统的作用)的刚度矩阵,[Kc(t)]为AVS系统的控制作用所产生的结构刚度矩阵的增量,由于每层的AVS构件只有“连接”和“断开”两种状态,所以[Kc(t)]可以表示为:
(2)
其中,ij(t)和[ΔKj]分别为:
[ΔKj]为第j层控制装置(即VSD)闭合所产生的结构刚度矩阵增量,n×n阶。
于是,结构的运动方程又可以写为以下形式:
即得到:
或:
(3)
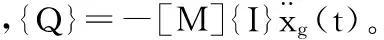
2 多模态控制算法及实现步骤
对于多自由度AVS系统,由于各层刚度、阻尼与相邻层的运动状态(位移、速度或加速度)耦连,在物理空间内设计控制算法较为困难,故该文利用独立模态空间控制法把对整个结构的振动控制转化为对少数低阶模态的控制。
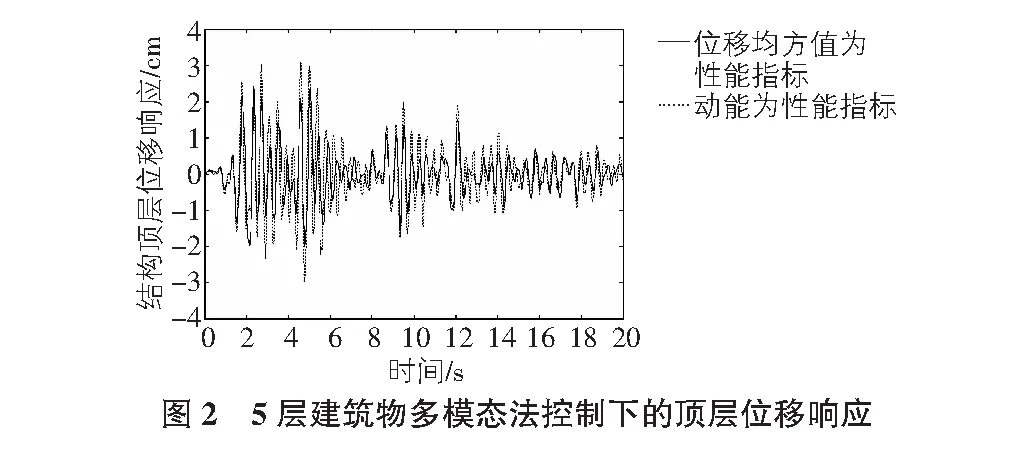
结构在地震作用下振动时,高阶模态反应一般很难被激发出来,所以仅考虑前r(r {x(t)}=[Φ]{q(t)} (4) 将式(4)代入式(3)并左乘[Φ]T得: (5) (6) (7) 由式(7)知结构的第i阶模态控制力[3]Fi为: (8) 将式(4)代入式(8)得: (9) 为了使方程解耦,以实现独立模态空间控制,现在忽略式(9)中的第二项,即令第i阶模态控制力Fi为: (10) 这样方程实现了解耦,但由于忽略了其他模态对第i阶模态控制力的影响,所以将产生解耦误差ei: (11) 该文将通过后面的算例对该解耦误差进行分析。 已知,式(10)中{φi}[Kc(t)]{φi}/mi表示控制刚度矩阵增量[Kc(t)]对第i阶模态位移qi(t)的影响,将其命名为控制影响因子,当[Kc(t)]分别取值为[ΔKj],即[Kc(t)]=[ΔKj],(j=1,2,…,m)时,{φi}T[ΔKj]{φi}/mi则表示第j层控制装置闭合(即第j层AVS构件起作用)对第i阶模态位移qi(t)的控制影响因子,记为: (12) 式(12)中(i=1,2,…,n,j=1,2,…,m),kj表示第j层AVS构件的刚度,φi,j-1和φi,j分别表示第i阶模态的第j-1和第j个分量。[ΔKj]表示第j层控制装置闭合而其他各层控制装置断开时,由于第j层AVS构件起作用而产生的结构刚度矩阵增量。 AVS系统的控制性能指标可采用势能或动能,下面通过算例分析对两种指标的控制效果进行比较,以确定效果较好的性能指标。 算例:剪切型建筑物的AVS控制。 考虑剪切型建筑物[4],结构的层数为n,每层的物理参数相同,分别为:层间质量mi=345.6 t,层间刚度ki=6.8×105kN/m,层间阻尼ci=734 kN·s/m,其中i=1,2,…,n。在每一层都设置AVS构件(钢性斜支撑),其下部固定于楼板,上部通过VSD与结构的横梁相连,各层AVS构件的连接刚度为Δki=6.8×105kN/m。地震动输入采用经调整的南北向El-Centro波,分析在前20 s内AVS控制下的结构响应,AVS控制的时间步长ΔT=0.02 s。本文用Matlab语言工具编制了AVS系统的控制算法(多模态法)程序,其中结构的时程分析依据了Newmark法[5]进行以下计算: 取结构的层数n=5,分别采用以质量阵加权的位移均方值和动能作为多模态法的性能指标,取模态控制阶数为r=3,计算建筑物在AVS控制下的地震响应。在性能指标1和性能指标2的AVS控制下,结构的最大顶层位移分别为2.42 cm和3.10 cm,最大顶层加速度分别为12.39 m/s2和21.25 m/s2,最大基底剪力分别为14 142 kN和22 709 kN。图2表示建筑物在两种控制性能指标下的顶层位移响应,其中实线表示位移均方值作为控制性能指标时的结构响应,点线表示动能作为控制性能指标时的结构响应。可以得出结论,位移均方值作性能指标的控制效果优于动能作性能指标的控制效果。由此,多模态法控制中均采用以质量阵加权的位移均方值作为AVS系统的控制性能指标。 通过算例分析,对多模态法作为AVS控制算法得出以下结论: 1)多模态法通过强行使运动方程解耦实现了独立模态空间控制,从而大大提高了AVS控制的运算速度,解决了在较高建筑中AVS控制的在线应用问题; 2)经比较,多模态法与枚举法作为AVS控制算法两种情况下的AVS控制效果相当; 3)对于很高的建筑物,用多模态法作为AVS控制算法的计算速度仍然有限,因此,在线控制问题有待于进一步研究。 [1] J.T.P. Yao.Conception of Structure Control, Journal of the Structure Division,ASCE,1972,98(7):1567-1574. [2] 何玉敖,冯得平.主动变刚度结构体系(AVS)多模态优化控制研究[J].建筑结构学报,2000,21(3):53-58. [3] 顾仲权,马扣根,陈卫东.振动主动控制[M].北京:国防工业出版社,1997. [4] J. N. Yang, J. C. Wu, Z. Li. Control of Seismic-excited Buildings Using Active Variable Stiffness Systems[J].Engineering Structures,1996,18(8):589-596. [5] 王勖成,邵 敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997. Active variable stiffness multi-modal control algorithm for tall buildings seismic design Zhang Yuexiang (ShanghaiTongjianQianghuaArchitectureDesignCo.,Ltd,Shanghai200092,China) An active variable stiffness multi-modal control algorithm is proposed based on kinetic performance control indicators. The control effect in tall buildings seismic design is studied based on numerical simulation analysis. It is found that the multi-modal control algorithm is effective and shorter online calculating time, solves on-line control in active stiffness control. tall buildings, seismic design, multi-modal 2015-03-10 张月香(1974- ),女,工程师 1009-6825(2015)14-0032-03 TU973 A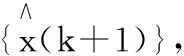
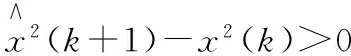
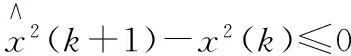
3 算例分析
4 结语
