双轮辙激励下多轴重型车辆动载特性仿真分析
2015-06-04刘祥银刘大维
刘祥银,陈 洋,高 攀,刘大维
(青岛大学 机电工程学院,山东 青岛 266071)
近年来,多轴重型车辆已成为主要的交通运输工具。车辆在公路行驶时,由于路面不平整而产生随机动载荷。路面受到移动的动态车轮荷载的反复作用,出现早期损坏、影响路面的使用寿命和服务能力。因此,正确获得动态车轮荷载是准确计算路面响应的关键环节之一。多年来,国内外许多学者对动态车轮荷载进行了大量的研究工作。如建立质量-弹簧-阻尼振动模型[1-5],或建立刚柔耦合的车辆多体动力学模型进行计算[6-8]。但在上述研究中,采用的是单轮辙或双轮辙时域路面激励输入,无法准确分析不同车速动态车轮荷载对路面的动态响应[9-10]。
本文采用有理函数功率谱密度的谐波叠加法构建双轮辙激励的空间域随机路面模型,并采用多体动力学仿真软件SIMPACK建立多轴重型汽车整车虚拟样机,研究空间频域双轮辙激励下多轴重型车辆动载特性,分析车辆以不同车速行驶时各轴两侧车轮的法向动载系数大小和变化规律,为今后研究多轴车辆随机动载荷作用下的路面动态响应提供参考依据。
1 双轮辙激励的空间域随机路面模拟
路面不平度具有随机、平稳和各态历经的特性,可以用功率谱密度函数表示路面不平度能量在空间频域的分布。
有理函数的路面位移单边功率谱密度为
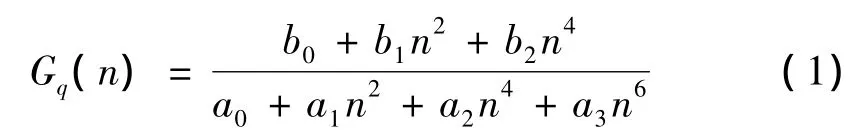
式中:b0、b1、b2、a0、a1、a2、a3为路面谱拟合多项式的系数;n为空间频率,m-1。
描述路面随机激励的方法主要有谐波叠加法、白噪声法、基于离散时间序列的AR/ARMA法和基于PSD离散采样的道路模拟方法等,本文采用谐波叠加法。
路面不平度的输入为[10]
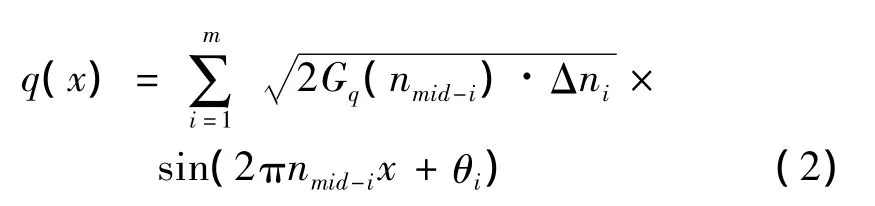
式中:nmid-i为将空间频率区间(n1,n2)划分成 m个小区间的中心频率;x为路面上任一点的纵向位置;θi为[0,2π]上均匀分布且相互独立的随机变量。
由于同一条道路相距为两侧车轮中心对称面距离的迹线都均具有随机、平稳和各态历经的特性,而且两迹线满足一定的相干特性[11-12]。因此,建立双轮辙激励空间域路面不平度模型时必须考虑其相干性。
假设一侧轮辙为x,另一侧轮辙为y,按式 (2)可得到一侧轮辙路面不平度的功率谱密度为Gqx(n),另一侧轮辙的路面不平度的功率谱密度为Gqy(n),则两个轮辙相干函数为
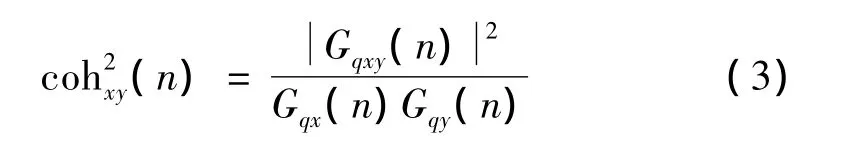
由式(3)可知,当相干函数确定后,即可求得另一轮辙激励的路面不平度的功率谱密度,最终得到另一轮辙激励的路面不平度。
本文利用多体动力学仿真分析软件SIMPACK路面生成器给出的双轮辙路面生成方法,取正弦波数为1500,正弦波的上、下截止空间频率为[0.01,2.83]m-1,路面功率谱密度拟合多项式的系数 b0=0.003743 9、b1=0、b2=0、a0=5.058896、a1=917.2805、a2=1、a3=0,可由 SIMAPCK 路面生成器建成如图1所示的240 m长双轮辙B级路面不平度曲线。通过对左、右两轮路面不平度数据进行相干分析,得到相干函数曲线如图2所示。
2 整车行驶系统动力学建模
建模时车辆为某公司生产的8×4轮系布置型式的双前桥重型载货汽车,其主要参数见表1所示。
建立整车多体动力学模型时,将车辆的轮胎、钢板弹簧视为柔体,车架、驾驶室等构件视为刚体;橡胶垫块、限位块简化为具有非线性刚度和阻尼特性的力元,忽略车辆动力装置的结构及振动对整车性能的影响。
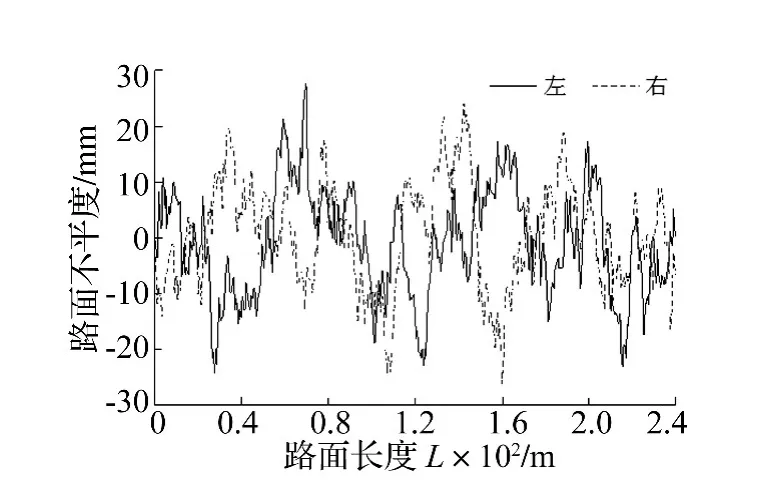
图1 B级路面不平度Fig.1 B-grade road surface
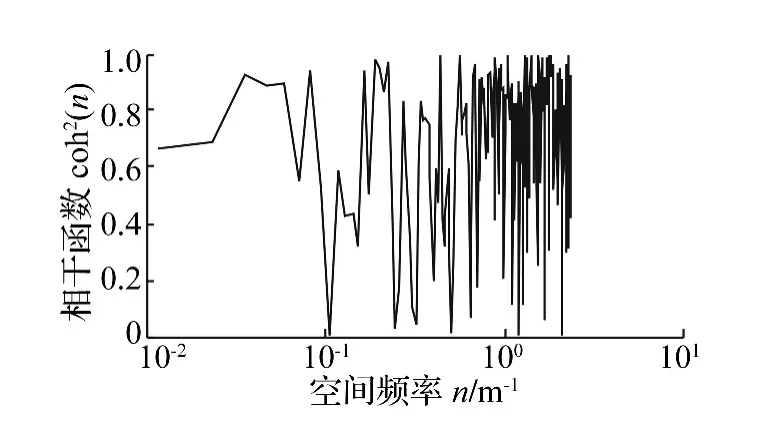
图2 双轮辙的相干函数曲线Fig.2 Coherence function
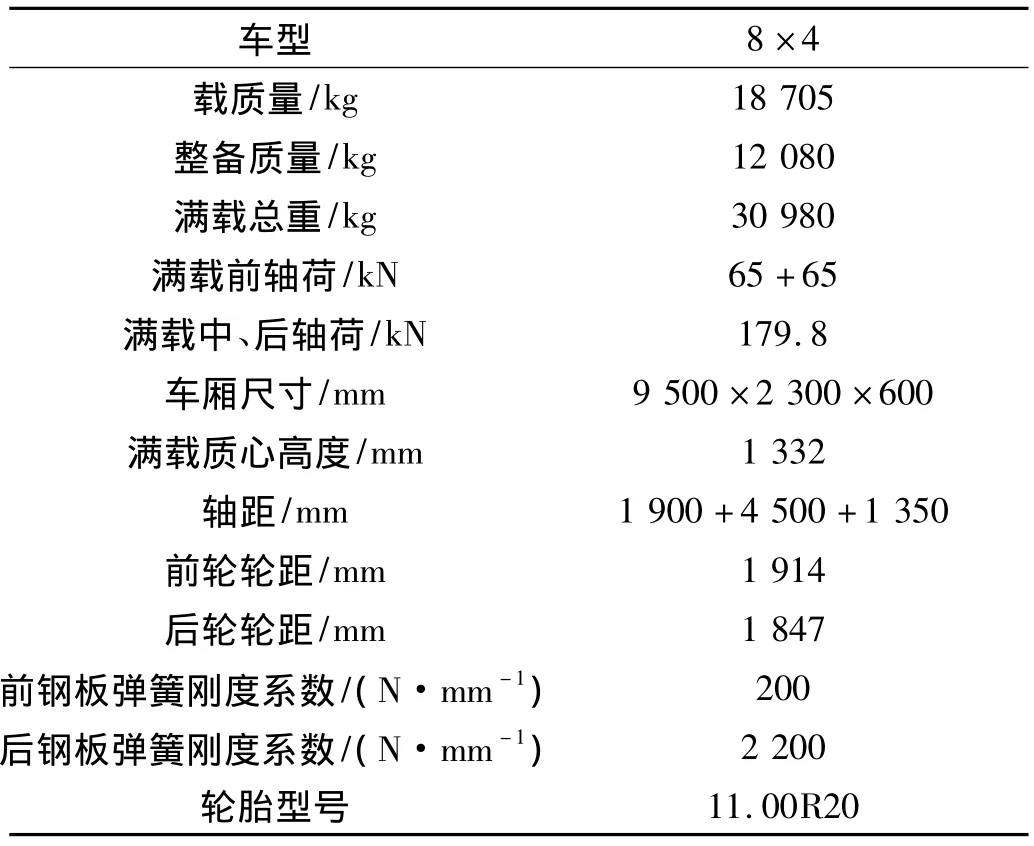
表1 整车参数Tab.1 Vehicle basic performance parameter
钢板弹簧柔体模型是利用SIMPACK软件中的离散体概念建立的,轮胎模型采用荷兰Delftt大学Pacejka教授提出的“魔术公式”轮胎模型[8]。
将在SIMPACK软件中建成的整车多体动力学模型和双轮辙随机路面模型集成,即可得到整车行驶动力学模型(见图3)。
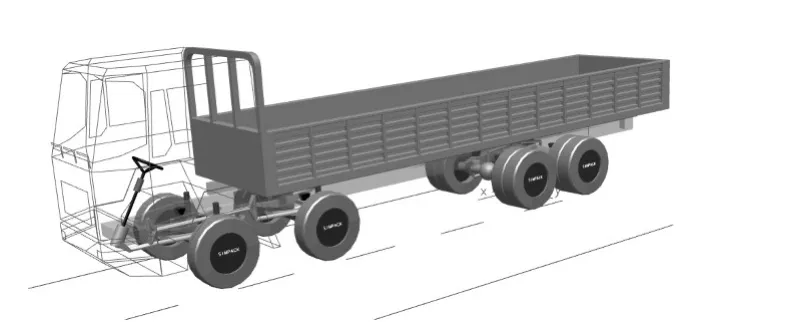
图3 整车行驶动力学模型Fig.3 Dynamic multi-body model of heavy vehicle
3 仿真结果及分析
3.1 轮胎法向作用力
图4给出了B级路面单轮辙激励和双轮辙激励下,车辆满载,行驶速度为60 km/h时,前轴、中前轴两侧轮胎的法向作用力随行驶距离的变化曲线。
由图4可看出,在单轮辙激励时,左、右两轮轮胎法向作用力的变化规律和大小基本相同;而在两轮辙激励时,左、右两轮轮胎法向作用力大小及变化规律不同,轮胎法向作用力最大值出现的位置也不同,且轮胎法向作用力波动较大。
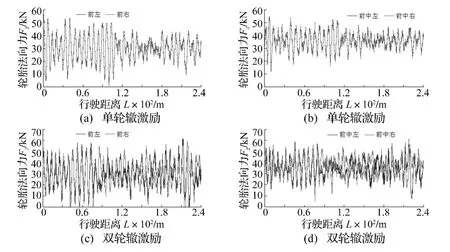
图4 两前轴轮胎法向作用力Fig.4 Dynamic normal tire force of two front axles
图5给出了B级路面单轮辙激励和双轮辙激励下,车辆满载,行驶速度为60 km/h时,中后轴、后轴两侧轮胎的法向作用力随行驶距离的变化曲线。
由图5可看出,无论单轮辙激励还是双轮辙激励时,中后轴和后轴轮胎法向作用力的变化规律和大小基本相同;但在两轮辙激励时,左、右两轮轮胎法向作用力的大小及变化规律不同,轮胎法向作用力最大值出现的位置也不同,且轮胎法向作用力波动较大。
由图4和图5还可看出,两前轴轮胎法向作用力数值小于中、后轴轮胎法向作用力的数值,前中轴轮胎法向作用力的波动程度最小,前轴、中后轴、后轴轮胎法向作用力波动程度较大。同时,在双轮辙激励时,中后轴、后轴轮胎法向作用力最小值接近于或等于0出现的次数较多。
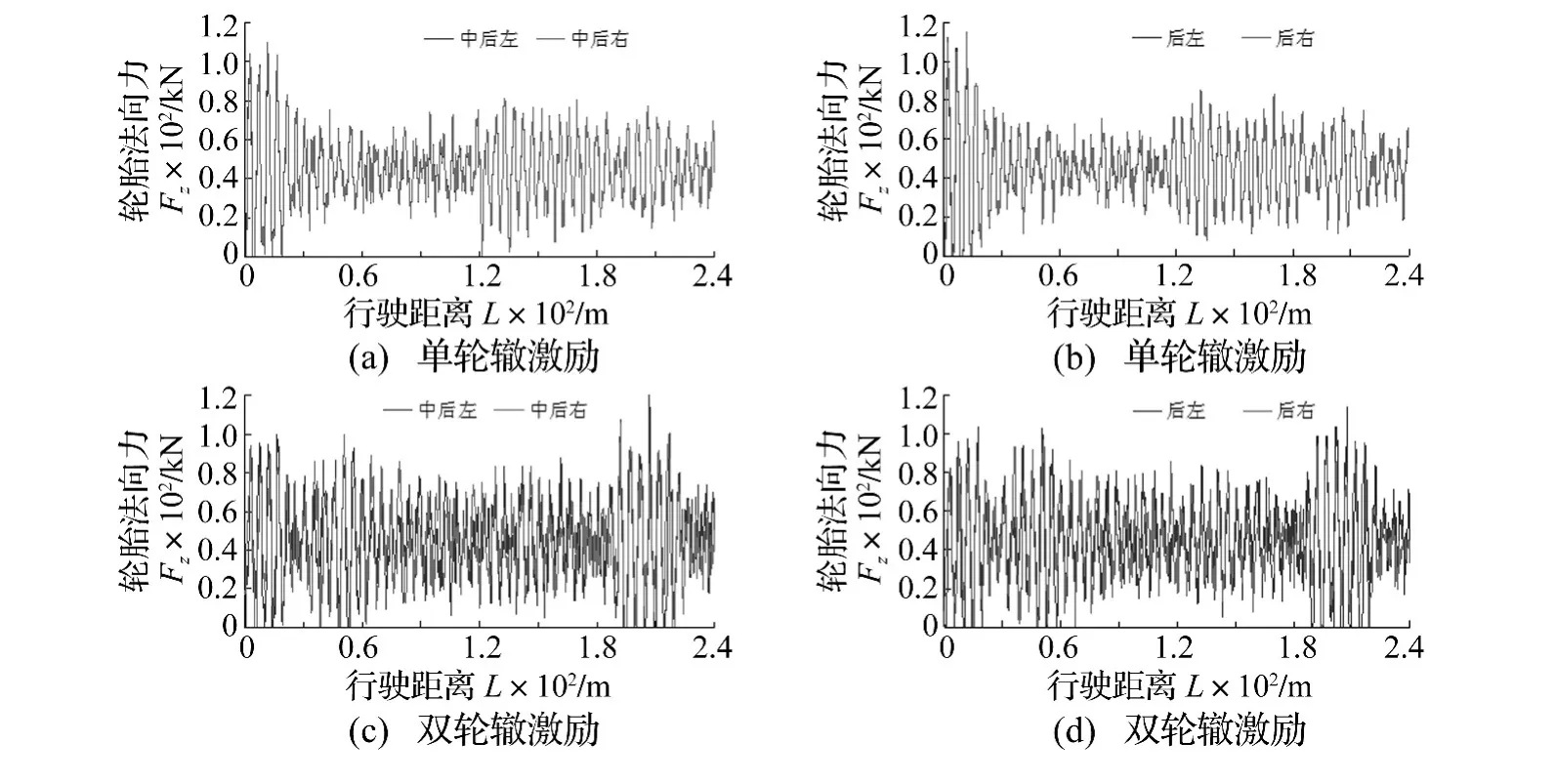
图5 两后轴轮胎法向作用力Fig.5 Dynamic normal tire force of two rear axles
3.2 车轮、车轴的法向动载系数
车轮法向动载系数D为

式中:Fjz为轮胎法向静载荷;σFd为轮胎法向动载荷均方根值。
车轴的法向动载系数D为车轴左右两侧车轮法向动载系数的平均值。
图6为B级路面单轮辙激励和双轮辙激励下,车辆行驶速度为50 km/h~90 km/h时,前、前中、中后、后车轴各车轮法向动载系数变化曲线。
由图6可看出,在单轮辙激励和双轮辙激励时,其车辆各轴两侧车轮的法向动载系数大小和变化规律完全不同。在单轮辙激励时,各轴左、右两轮法向动载系数均随行驶速度的提高均呈增加趋势,前中轴车轮法向动载系数最小,前、中后、后轴车轮法向动载系数相差不大;在双轮辙激励时,前中轴左、右两侧车轮法向动载系数随行驶速度的提高变化不大,但数值有一定差别;而前、中后、后轴的左、右两侧车轮法向动载系数随行驶速度的提高变化比较复杂,前、中后、后轴的左、右两侧车轮法向动载系数变化规律和数值差别较大,前轴右侧车轮的法向动载系数在车速60 km/h~70 km/h变化很小;中后、后轴的左侧车轮法向动载系数在车速为70 km/h时,随车速的增加而减小,且车轮法向动载系数小于中后、后轴的右侧车轮法向动载系数。
图7为B级路面单轮辙激励和双轮辙激励下,车辆行驶速度为50 km/h~90 km/h时,前、前中、中后、后车轴的法向动载系数变化曲线。
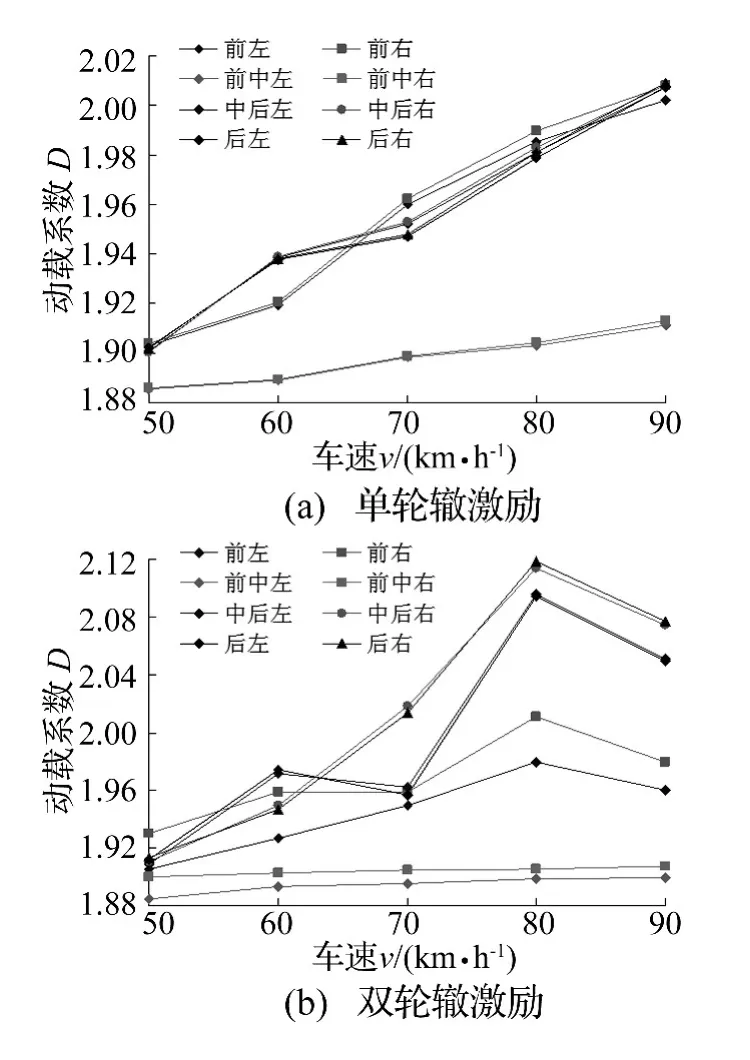
图6 车轮法向动载系数Fig.6 Tire normal dynamic load coefficients
由图7可看出,在单轮辙激励时,其各车轴的法向动载系数大小和变化规律与各轴两侧车轮的法向动载系数大小和变化规律基本相同;在双轮辙激励时,其各轴车轮的法向动载系数大小和变化规律与各轴两侧车轮的法向动载系数大小和变化规律不完全不同。中后、后两轴的法向动载系数基本相同;在车速超过80 km/h后,前、中后、后车轴法向动载系数开始下降。
图8为双轮辙激励与单轮辙激励相比,车辆行驶速度为50 km/h~90 km/h时,前、前中、中后、后车轴法向动载系数变化程度的曲线。
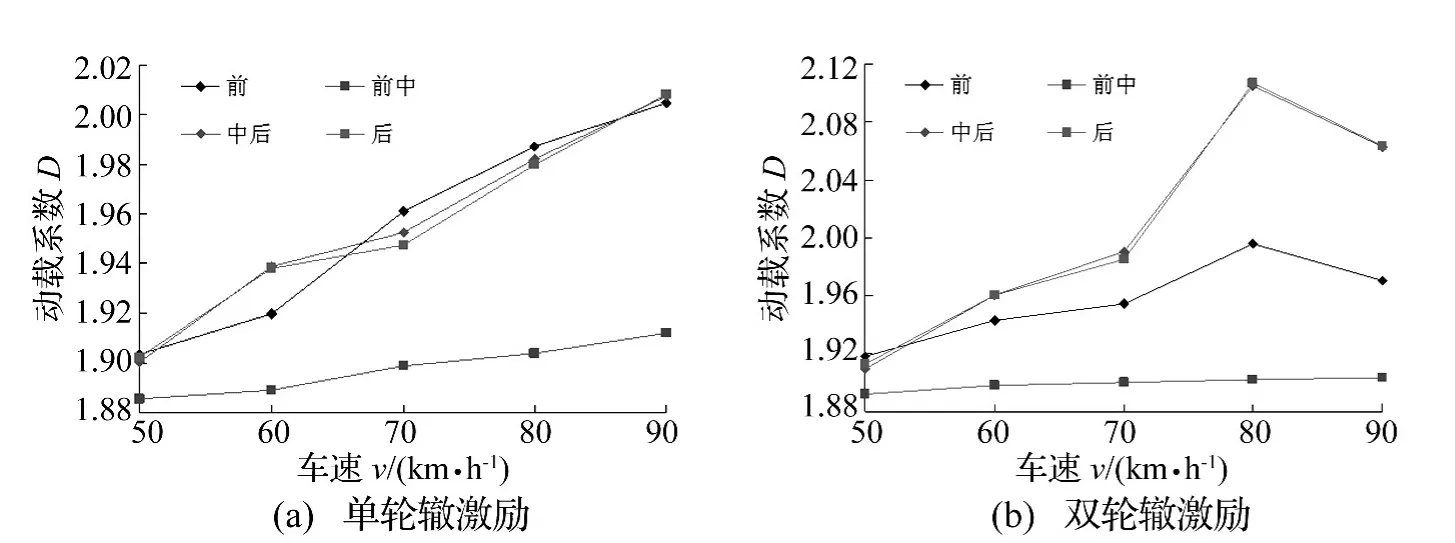
图7 车轴法向动载系数Fig.7 Vehicle axle normal dynamic load coefficient
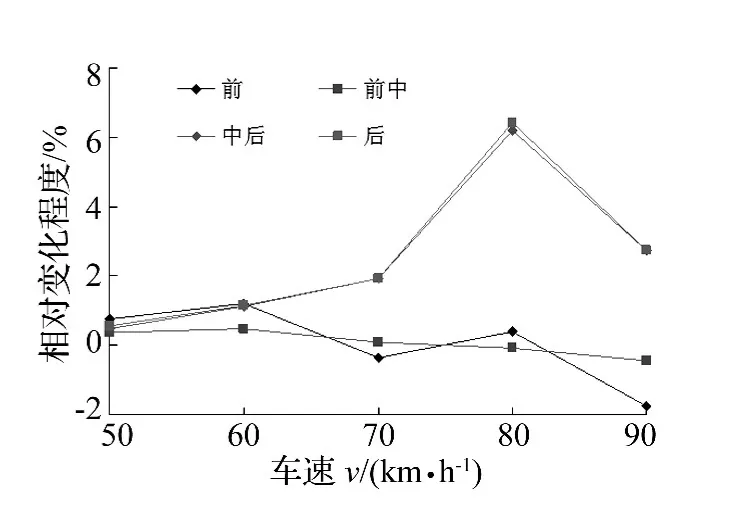
图8 双轮辙激励相对单轮辙激励的车轴法向动载系数变化程度对比Fig.8 The contrast of vehicle axle normal dynamic load coefficient between bilateral tracks’road excitation and single tracks’road excitation
由图8可看出,双轮辙激励与单轮辙激励相比,车辆行驶速度为50 km/h~90 km/h时,前轴法向动载系数相对变化范围为-1.74% ~1.90%、前中轴法向动载系数相对变化范围为-0.44% ~0.47%、中后轴法向动载系数相对变化范围为0.49% ~6.19%、后轴法向动载系数相对变化范围为0.55% ~6.41%。
4 结论
(1)采用了有理函数功率谱密度的谐波叠加法模拟双轮辙激励的空间域随机路面,并集成创建一个双轮辙激励的空间域路面车辆行驶动力学模型,仿真计算了车辆各轴两侧车轮的法向作用力和车轮法向动载系数。
(2)分析了单轮辙和双轮辙激励下车辆各轴两侧轮胎法向作用力的大小和变化规律。双轮辙激励下,车辆各轴两侧轮胎法向作用力的大小和变化规律均不相同,而且轮胎法向作用力最大值出现的位置也不同。
(3)双轮辙激励下,车辆在不同车速时各轴两侧车轮的法向动载系数大小和变化规律完全不同,车辆前中轴的法向动载系数最小,中后、后轴的法向动载系数最大。
(4)研究结果可为精确计算多轴车辆轮胎动载荷,预测路面动态响应提供参考依据。
[1]吕彭民,尤晋闽,和丽梅.路面随机不平度下车辆对路面的动载特性[J].交通运输工程学报,2007,7(6):55 -58.LÜ Peng-min,YOU Jin-min,HE Li-mei.Vehicle dynamic load property resulted from road random roughness[J].Journal of Traffic and Transportation Engineering,2007,7(6):55 -58.
[2]王直民,张土乔,吴小刚.不平整路面上的车辆等效动载系数[J].浙江大学学报(工学版),2007,41(6):1007-1011.WANG Zhi-min,ZHANG Tu-qiao,WU Xiao-gang.Equivalent vehicle dynamic load coefficient on rough pavement[J].Journal of Zhejiang University(Engineering Science),2007,41(6):1007-1011.
[3]曹源文,梁乃兴,于清,等.路面不平整引起的车辆动载计算方法[J].交通运输工程学报,2008,8(2):69 -73.CAO Yuan-wen,LIANG Nai-xing,YU Qing,et al.Calculating method of vehicle dynamic load caused by uneven pavement[J].Journal of Traffic and Transportation Engineering,2008,8(2):69-73.
[4]Kropác O,Múcka P.Effect of obstacles in the road profile on the dynamic response of a vehicle[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2008,222(3):353 -370.
[5]秦旻,梁乃兴,陆兆峰,等.动荷载作用下沥青路面寿命预估[J].公路交通科技,2010,27(3):34 -38.QIN Min,LING Nai-xing,LU Zhao-feng,et al.Remaining life prediction of asphalt concrete pavement under dynamic load[J].Journal of Highway and Transportation Research and Development,2010,27(3):34 -38.
[6]刘大维,刘伟,陈焕明,等.基于多体模型的重型车辆对路面的动载特性[J].农业机械学报,2009,40(11):7 -12.LIU Da-wei,LIU Wei,CHEN Huan-ming,et al.Dynamic load characteristics of heavy vehicle based on multi-body dynamic model[J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(11):7 -12.
[7]刘大维,陈焕明,刘伟,等.基于整车多体模型的重型车辆对路面的损伤评价[J].振动与冲击,2010,29(4):92-96.LIU Da-wei,CHEN Huan-ming,LIU Wei,et al.Evaluation of road damage based on full heavy vehicle multi-body dynamic model[J].Journal of Vibration and Shock,2010,29(4):92-96.
[8]何兆益,刘炳森,杜子学,等.重型车辆与路面耦合作用的仿真分析研究[J].公路交通科技,2009,26(3):22 -26.HE Zhao-yi,LIU Bing-sen,DU Zi-xue,et al.Analysis of coupling vibration caused by heavy-duty vehicles and road pavement[J].Journal of Highway and Transportation Research and Development,2009,26(3):22 -26.
[9]Shi X M,Cai C S.Simulation of dynamic effects of vehicles on pavement using a 3D interaction model[J].Journal of Transportation Engineering,2009,135(10):736 -744.
[10]蒋荣超,刘大维,王松,等.时域和空间域路面激励下重型车辆动载荷仿真分析[J].公路交通科技,2012,29(5):152-158.JIANG Rong-chao, LIU Da-wei, WANG Song,et al.Simulation analysis of heavy vehicle dynamic load under road excitation[J].Journal of Highway and Transportation Research and Development,2012,29(5):152 -158.
[11]Sun L.Optimum design of“road-friendly”vehicle suspension systems subjected to rough pavement surfaces[J].Applied Mathematical Modelling,2002,26(5);635 -652.
[12]王亚,陈思忠,郑凯锋.时空相关路面不平度时域模型仿真研究[J].振动与冲击,2013,32(5):70 -74.WANG Ya,CHEN Si-zhong,ZHENG Kai-feng.Simulation research on time domain model of road roughness with timespace correlation[J].Journal of Vibration and Shock,2013,32(5):70-74.
