钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度

毛 亮，王 华，姜春兰，李 明

(1.北京航空航天大学 宇航学院，北京 100083;2.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

现代高科技战争对武器系统的机动性及防护能力要求日益提高，传统的单一均质金属装甲由于受到固有结构的限制，已不能满足现代武器装备发展的需要，各种非金属复合装甲由于其良好的综合性能而成为现代装甲的主要防护结构［1］。

陶瓷材料具有高强度和高弹性模量的特性，早在20世纪60年代就被用作防护材料，但由于其易碎性，不能承受多次命中贯穿的能力，因而不能单独作为防弹装甲材料，必须有背板作为支撑底板才能发挥陶瓷优越的抗弹性能［2－5］。理想的背板既要有足够的刚性支持面板，又要能有效的吸收动能。纤维增强树脂基复合材料是用树脂作基体，由各种纤维增强的先进复合材料。它比重小，比强度、比模量高以及良好的抗弹性能和抗高压性能，使其成为最佳背板材料之一。近年来，继碳纤维、玻璃纤维、硼纤维和芳纶纤维之后，又出现了一种高性能纤维——超高分子量聚乙烯(Ultrahigh Molecular Weight Polyethylene Fiber，UHMWPE)纤维［6－8］，它是一种由平均相对分子质量在100万以上的聚乙烯纺制而成的纤维。该纤维除了具有高强度、高模量的特点以外，还具有良好的耐化学腐蚀、比能量吸收高、电磁波透射率高、摩擦系数低、优良的耐冲击和抗切割性能，以及不吸水、与生物相容性好等特点，并且是所有高强高模纤维中相对密度最小的纤维。因此，利用UHMWPE制备而成高强聚乙烯纤维增强树脂基层合板(DFRP)附上陶瓷防护层，将具备良好的抗侵彻性能。

钨合金球形破片由于密度大，保持速度和穿甲的能力强，已逐渐成为当前杀伤战斗部的首选毁伤元素。为此，本文针对钨合金球形破片垂直碰撞不同厚度组合的陶瓷/DFRP复合靶的弹道极限速度开展了实验研究，并结合量纲分析方法建立了弹道极限速度经验关系。研究结果对战斗部的优化设计以及轻型装甲防护结构的优化设计都具有十分重要的应用价值。

1 弹道实验

1.1 弹靶材料

本实验采用2 g(直径φ6mm)的钨合金(93W－Ni－Fe)球体作为侵彻体，陶瓷采用北京大华陶瓷厂生成的3mm～10mm厚的Al2O3陶瓷，聚乙烯纤维增强树脂基复合材料为荷兰DSM公司生产的超高分子量聚乙烯纤维系列Dyneema UD77。各材料具体性能参数如表1～表3所示。

表1 钨合金球体材料性能参数Tab.1 Performance parameters of tungsten alloy sphere

表2 Al2 O3陶瓷材料性能参数Tab.2 Performance parameters of Al2 O3 ceramic

表3 纤维材料性能参数Tab.3 Performance parameters of fiber

1.2 靶板制备

聚乙烯纤维增强树脂基复合材料层合板(DFRP)制备采用热压工艺，首先将Dyneema UD75预浸料按设计要求裁成一定尺寸，并正交铺层至所需厚度，放入模具中;然后将模具置于热压机上，升温速率为(2～3)℃/min，当温度稳定在120℃后，保温、加压;30 min后，自然冷却至室温、卸模。根据所铺预浸料层数不同将会得到不同面密度的层合板。

陶瓷/DFRP复合靶的结构如图1所示，在陶瓷表面粘附由尼龙纤维复合材料制成的止裂层，而且各靶层之间铺一层航空胶膜，最后将铺设好的复合靶放入高温高压炉中压合而成。

图1 陶瓷/DFRP复合靶结构示意图Fig.1 Sketch map of ceramic/DFRP composite target

1.3 实验装置

实验装置及其布置如图2所示，它包括破片专用发射器、防护装置、破片速度测试系统、靶架和残余体回收装置等。破片专用发射器为12.7mm的弹道枪，速度由发射药量来控制。为保证发射所必须的密封性和达到规定的速度，钨合金球被置于凹形的尼龙弹托中，待弹托飞离枪口后，在空气阻力作用下钨球与弹托分离，弹托自身也因受冲击而破碎，破碎后的弹托碎片会被防护板拦截，而球则通过防护板中心处小孔飞向靶板，球的撞靶速度及残余体速度分别由靶前和靶后的一组测速靶网和时间测试仪器来完成。当撞击速度大于弹道极限速度时，球贯穿靶板后，其残余体和冲塞以及靶背面的崩落碎片将由残余体回收装置收容。

图2 实验装置布置示意图Fig.2 Sketch map of experimental arrangement

1.4 实验结果及处理

破片对靶板弹道极限速度的大小，是衡量破片对靶板作用效果的重要指标，是评价弹药威力的主要参量［9－10］。它指破片部分侵入靶板的最高速度和完全穿透靶板的最低速度的平均值，破片侵彻靶板的弹道极限速度可用v50或v100来表征［11］。大量实验证明，对于给定的弹靶系统，v50服从正态分布，当未贯穿数大于或小于贯穿数时，v50的计算公式分别为

式中:vA为贯穿与未贯穿的混合区内所有速度的平均值;Np为混合区内未贯穿破片数，Nc为贯穿破片数;vpmax为未贯穿破片的最大速度;vpmin为贯穿破片的最小速度。

在上述实验方案的基础上，采用钨合金球形破片对不同面密度的陶瓷/DFRP复合靶板，进行了不同撞击速度下的弹道性能实验，获得了相应的弹道极限速度，具体结果如表4所示。

图3给出了不同结构陶瓷/DFRP复合靶的弹道极限速度随靶板面密度的变化，图4为弹道极限速度时靶板的吸能情况，其中，Ea为靶板吸收的能量，m为钨合金球形破片的质量，v50为弹道极限速度。此外，图中还给出了钨合金球破片侵彻均质装甲钢的弹道极限速度的实验结果(见文献［12］)。

表4 陶瓷/DFRP复合靶结构尺寸及弹道极限速度值Tab.4 Structure size and ballistic limit velocity of ceramic/DFRP composite target

图3 陶瓷/DFRP复合靶的弹道极限速度［12］Fig.3 Ballistic limit velocity of ceramic/DFRP composite target［9］

图4 陶瓷/DFRP复合靶的能量吸收特性［12］Fig.4 Energy absorption characteristics of ceramic/DFRP composite target［9］

2 侵彻相似律分析

2.1 量纲分析法及侵彻相似律

量纲分析法是在研究现象相似性问题的过程中，对各种物理量的量纲进行观察时产生的。它的理论基础是关于量纲齐次的方程的数学理论［13］。一般用于说明物理现象的方程都是齐次的，这也是Π定理得以通过量纲分析导出的基础。但Π定理一经导出，便不再局限于带有方程的物理现象。通过量纲分析法考察其量纲，可求得和Π定理一致的函数关系式并据此进行相似现象的推广。量纲分析的这个优点，对那些机理尚未弄清、规律也未充分掌握的复杂现象来说尤其明显。它能帮助人们快速地通过相似性试验核定所选参量的正确性，并在此基础上不断加深人们对现象机理的规律性认识。

针对钨合金球形破片垂直侵彻不同厚度结构的陶瓷/DFRP复合靶，首先分析决定侵彻过程的独立物理量，然后根据Π定理确定控制侵彻过程的独立相似参数，在此基础上，进一步讨论几何相似律成立应遵循的条件。

球形破片垂直侵彻陶瓷/DFRP复合靶的过程与许多参数有关，若忽略一切热效应，则决定弹道极限速度的主要独立物理量如表5所示。

破片侵彻靶板的现象和过程是极其复杂的，对有限厚度复合结构靶板的侵彻更是如此。由于复合材料的各向异性，有关侵彻力学的许多问题至今利用解析法尚不能全部解决或者根本无法解决。目前关于复合材料以及陶瓷复合靶的侵彻理论计算和数值分析仍是一个人们正在探讨的研究课题，因此，在对复合材料及陶瓷复合靶侵彻力学问题的研究中，需要在实验研究的基础上，搞清支配侵彻过程的主要影响因素和内在本质，并建立起能满足实际应用的工程计算式。

表5 决定弹道极限速度的独立物理量Tab.5 Independent physical quantities of controlling ballistic limit velocity

由此可知，钨合金球体垂直侵彻有限厚陶瓷/DFRP复合靶的弹道极限速度是上面24个物理量的函数，即

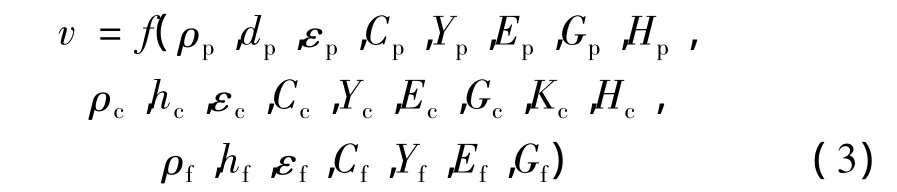
选取dp、ρp和Yp为独立量纲物理量，则根据量纲齐次原则，其它导出量可改写成无量纲形式如下

根据量纲分析Π定理，将方程(3)改写成无量纲参数表示的关系式，则

可以看出，Π1～Π6、Π8～Π15、Π17～Π21只与材料性质有关，在球体和靶板材料确定的情况下，上述19个相似参数自行满足。因此，方程(4)可简化为

2.2 弹道极限速度经验关系式

从前面的分析可知，在球、靶材料不变条件下，钨合金球形破片侵彻陶瓷/DFRP复合靶板的弹道极限速度应遵从几何相似律，即球侵彻靶板的无量纲弹道极限速度仅是靶板厚度和球初始直径的函数。于是，由式(5)可知，

式中:K、α、β为待定常数。为了便于拟合，令

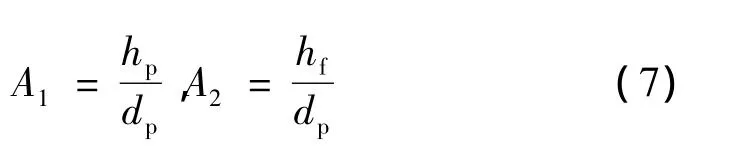
则式(6)可写为

两边同时取对数，得

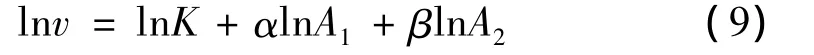
再令

则

利用弹道实验结果，对式(11)进行多元线性回归，并将回归得到的各系数代入式(6)，从而得到钨合金球形破片垂直侵彻陶瓷/DFRP复合靶板的弹道极限速度工程经验关系式为

上式中v即为v50，由于式(12)是在量纲分析的基础上，根据实验结果拟合分析得到的，因此它适用于钨合金球形破片对陶瓷/DFRP复合靶的侵彻贯穿，适用参数范围为 v ＜ 1200 m/s，0.52 ＜ hc/dp＜ 1.52。表 6 和图5给出了钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度的实验值与用式(12)计算结果的比较。

从表6中的数据可以看出，对于钨合金球形破片－陶瓷/DFRP复合靶系统，弹道极限速度计算值与实验值的相对误差平均值为小于2.7%，最大单项误差为3.8%，满足工程应用要求。

表6 钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度的实验值与计算值的比较Tab.6 Comparison between experimental and calculated values of ballistic limit velocity

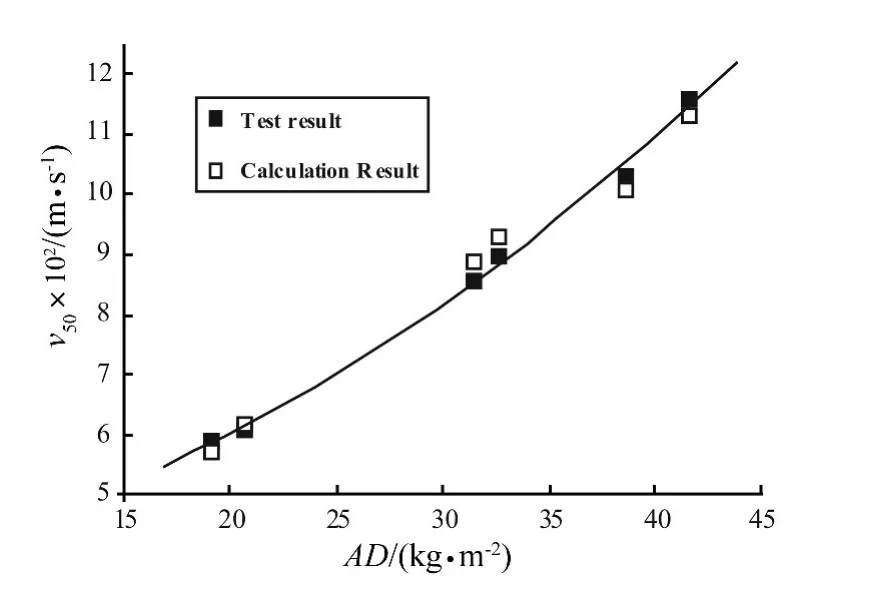
图5 钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度的实验值与计算值的比较Fig.5 Comparison between experimental and calculated values of ballistic limit velocity

3 结论

通过以上研究，得到主要结论如下:

(1)随着陶瓷/DFRP复合靶面密度的增加，其弹道极限速度和靶板吸收的弹道能也增加;此外，在相同面密度下，陶瓷/DFRP复合靶的抗钨合金球破片侵彻弹道特性要明显优于均质装甲钢板。

(2)借助量纲分析法和相似理论得到了钨合金球形破片侵彻陶瓷/DFRP复合靶的弹道极限速度经验关系式，其计算结果与实验值符合较好，满足工程计算要求，对战斗部及装甲防护结构的优化设计与计算具有重要的应用和参考价值。

［1］张震英，戴芳.复合材料在坦克装甲车辆上的应用［J］.塑料，2000，29(3):38－42.ZHANG Zhen－ying，DAI Fang.Applications of composite in the armored vehicles［J］.Plastics，2000，29(3):38 －42.

［2］宜晨虹，胡美娥，谷岩.93钨破片高速侵彻陶瓷/铝合金复合结构实验研究［J］.兵器材料科学与工程，2013，36(3):17－19.YI Chen－hong，Hu Mei－e，Gu Yan.High velocity penetration of ceramic/aluminum composite structure by 93 tungsten fragment［J］.Ordnance Material Science and Engineering，2013，36(3):17－19.

［3］Roseberg Z，Tsaliah J.Applying Tate’s model for the interaction of long rod projectiles with ceramic target［J］.Int J Impact Eng，1990，9(2):247－251.

［4］Woodward R L. A simple one－dimensional approach to modeling ceramic composite armour defeat［J］.Int J Impact Eng，1990，9(4):455－474.

［5］Chocron Benloulo I S，Sanchez－Ánchez－Gálvez V.A new analytical model to simulate impact onto ceramic/composite armors［J］.Int.J.Impact Engng，1998，21(6):461－471.

［6］郑震，施楣梧，周国泰.超高分子量聚乙烯纤维增强复合材料及其防弹性能的研究进展［J］.合成纤维，2002，31(4):20－26.ZHENG Zheng，SHI Mei－wu，ZHOU Guo－tai.Progress in ultrahigh molecular weight polyethylene fiber reinforced composites and its bulletproof property［J］.SFC，2002，31(4):20－26.

［7］王晓强，朱锡，梅志远.高速钢质破片侵彻高强聚乙烯纤维增强塑料层合板试验研究［J］.兵工学报，2009，20(12):1574－1578.WANG Xiao－qiang， ZHU Xi， MEI Zhi－yuan. An experimentalresearch on high velocity steel fragments perforation UHMEWPE FRP laminates［J］. Acta Armamentarii，2009，30(12):1574 －1578.

［8］陈长海，朱锡，王俊森，等.高速钝头弹侵彻中厚高强聚乙烯纤维增强塑料层合板的机制［J］.复合材料学报，2013，30(5):226－235.CHEN Chang－hai， ZHU Xi， WANG Jun－sen， et al.Mechanism of high－velocity blunt－nosedprojectiles penetration moderately thick UHMWPE fiber reinforced plastic laminate［J］.Acta Materiae Compositae Sinca，2013，30(5):226 －235.

［9］王海福，刘志雄，冯顺山.钢球侵彻钛合金靶板弹道极限速度［J］.北京理工大学学报，2003，23(2):162－164.WANG Hai－fu，LIU Zhi－xiong，FENG Shun－shan.Ballistics limit velocity for spherical steel fragments penetrating titanium－alloy target plates［J］.Transact Ions of Beijing Institute of Technology，2003，23(2):162－164.

［10］徐豫新，王树山，伯雪飞，等.钨合金球形破片对低碳钢的穿甲极限［J］.振动与冲击，2011，30(5):192－195.XU Yu－xin，WANG Shu－shan，BO Xue－fei，et al.Armorpiercing ultimate of tungsten alloy spherical fragment against low－carbon steel［J］.Joural of Vibration and Shock，2011，30(5):192－195.

［11］美国陆军器材部.终点效应设计［M］.李景云，习春，于骐，译.北京:国防工业出版社，1988:218－225.

［12］午新民.钨合金球体对有限厚靶板侵彻的理论和实验研究［D］.北京:北京理工大学，1997.

［13］欧阳楚萍，徐学华，高森烈.相似与弹药模化［M］.北京:兵器工业出版社，1995:38－62.