荣成地震台形变观测资料小波分析

徐芳芳 崔居全 荆 强 安巴雅尔 孙宗强

1)中国山东 264300 荣成地震台

2)中国山东 264000 威海市地震局

3)中国云南 657800 水富县防震减灾局

0 引言

小波分析(wavelet analysis)是目前信号处理分析的重要方法，在时频两域具有表征信号局部特征的能力，是一种窗口大小固定不变而形状可改变，时间窗和频率窗均可改变的时频局部化分析方法，即在低频部分具有较低的时间分辨率和较高的频率分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，适于分析非平稳信号和提取信号的局部特征。宋治平等（2003）、李杰等（2005）、张燕等（2004，2009）、李艳等（2011）、张军等（2011）对数字化地壳形变前兆资料进行一系列研究，并取得一定成果，可见小波变换理论对地震前兆观测资料分析具有广阔的应用前景。

采用Matlab软件，运用小波分析方法，对荣成地震台（以下简称荣成台）CZB-Ⅱ竖直摆钻孔倾斜仪观测资料进行处理，研究形变数据的波动、人为标定、同震响应、固体潮等。根据以往研究成果，采用db4作为母小波，对形变观测资料进行4—7层小波分解，近似部分清晰可见数据趋势变化，细节部分能清晰显示包括1/4日波、半日波、日波和半月波等在内的固体潮汐波，并能清晰可见数据中固体潮汐波的周期特征及随时间变化情况。

1 小波分析理论

1.1 小波变换理论及小波基函数选取

实际工作中数据信号是离散的，需要对信号进行离散小波变换DWT（Discrete Wavelet Transform）。对于离散序列信号f(x)，在小波函数ψ(t)∈L2(R)中，尺度因子(伸缩因子a和平移因子b）（a，b∈R）也需要离散化，则应用小波变换作为不同频率的信息识别基础（宋志平等，2003），即

在资料处理中，采用a=2k。随着k的增加，信号从最高频向低频分解。当k=0时，信号为采样频率；k=1时将频率二等分，依此类推。

对于数字信号f(x)，可以近似表示为

小波分解的快速算法称为马拉( Mallat) 算法。Mallat 算法（薛志芳等，2012）在小波分析中的地位相当于快速傅里叶变换算法在经典傅里叶分析中的地位。Mallat 算法为正交展开系数 与 分别满足以下关系。

而Mallat重构算法为

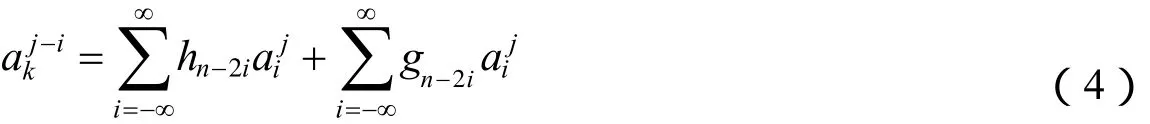
式中，hn与gn分别是尺度函数和小波函数滤波器，且=h-n，=g-n。

小波基不是唯一的，其选取没有明确标准，选择合适的小波基进行信号处理需要考虑其正则性和消失矩、所处理信号与小波基的相似性等因素，正交小波变换对此优势较大。Daubechies小波是离散正交小波，可表示为dbN，其中N是小波的阶。dbN不具对称性（即非线性相位），没有明确的解析表达式，小波函数ψ与尺度函数φ的有效支撑长度为2N－1，ψ的消失矩为N。根据以往研究结果（宋治平，2003；李杰等，2005），发现db4小波就提取形变资料异常效果较好，故本研究继续采用db4小波。

1.2 频率分析

图1 小波分解近似及细节部分与频率关系Fig.1 Relationship among approximation part, detail part and frequency of wavelet decomposition

小波变换系数与实际为窗口小波变换。当j固定时，随着k的变化，与均占满时间域未重叠；随着j的变化， 占满频率域未重叠。

设信号f(x)在时间域[0，T]采样，共采N个点，采样间隔为Δt=T/N。{fi}(i=0，1，…，N－1)的频带为[0，Ω]，求出近似部分的系数{}(k=0，1，…，N－1)，其频带为 [0，Ω]。频带为 [0，Ω]，频带为[0，Ω/2]，的频率为 [Ω/2，Ω]，以此类推，与的频带分别为 [0，Ω/2j]与 [Ω/2j，Ω/2j-1](图 1)。

通过小波变换方法可对不同频率范围内的信息进行识别与分离。根据公式(4)及小波分解的近似部分(x)与细节部分(x)与频率的关系（图1），对观测资料进行近似部分(低频)与细节部分(高频)信息分离。根据观测量的物理含义，在分析干扰因素的基础上，从近似部分中确定趋势变化信息，从细节部分识别短期异常。

2 小波分析

荣成台位于山东半岛最东端，地处海西头—俚岛断裂西南15 km，乳山断裂东80 km，构造涉及胶辽断块南部和北黄海凹陷，距离东部海域6 km。台站安装3套形变仪器，TJ-Ⅱ体应变仪于2006年9月安装运行，2012年6月因探头故障停测；CZB-Ⅱ竖直摆钻孔倾斜仪位于荣成台院内西侧，2007年7月正式运行；RZB-Ⅱ分量应变仪位于院内西南角，于2014年12月24日安装运行，因运行时间较短，主要采用竖直摆倾斜仪数据。本研究选择仪器运行以来正常、固体潮清晰、数据连续可靠的形变测项的月小时或分钟值及日分钟值数据进行小波分析，对个别缺数进行线性插值处理，保证资料的连续可靠。

2.1 高频与低频信息识别

图2为倾斜仪北南分量2014年5月—10月整点值曲线及小波变换的4阶a4近似部分和d1—d4细节部分。从细节部分看出，1阶信号主要为最高频率信息，包含突跳干扰、噪声信号等，2阶信号可以看出1/4日波、半日波、日波信息；3阶、4阶信号可以看出半日波、日波、半月波信息，从4阶近似部分可以看出数据的变化趋势。由图2可见，2014年6月13日因数采面板电压不稳定，数据出现阶变；7月24—25日降大暴雨，降雨量达243 mm，因降雨地面上覆土层荷载增大，数据出现阶变。由此可知，细节部分主要反映固体潮汐半日波、日波、半月波的高频变化信息，近似部分信息反映整体趋势变化过程，因此可以将小波分析用于地震前兆观测资料年变趋势对比分析，寻找长期异常变化。可见，应用小波分析可对不同频率范围内的信息进行有效识别。

图2 2014年5—10月数据小波变换近似部分和细节部分Fig.2 Inclinometer NS direction data wavelet approximation part and detail part from May to Oct.，2014

2.2 不同频率信息分离

借助 Matlab（2013）小波分析软件，以倾斜仪北南分量2014年4月的分钟值为例，对形变观测资料进行近似部分（低频）与细节部分（高频）信息的分离。图3分别给出倾斜仪分钟值原始信号s、小波变换低频（a1，a2，…，a5）与高频（d1，d2，…，d6）曲线。随着分离层数的增加，高频信息被剔除，使固体潮信号随时间尺度的变化趋势更加明显、直观，清晰显示数据固体潮信息特征。图3(a)给出不同频率范围的近似部分（低频）信息，反映数据整体变化趋势。图3(b)给出不同频率范围细节（高频）部分，反映数据短期变化趋势。从图3清晰可见，4月的数据有6次同震效应，包括大震远震和近中、小地震，经过6阶分解，可消除地震同震效应产生的影响。由图3(a)可见，数据经过6阶分解后，干扰消除，显示出原始变化趋势，清晰可见4月26—28日因降雨影响数据出现的趋势转折，并能准确看出受降雨影响的时间段。

选取图3中两种代表性数据进行处理：①同震效应：2014年4月2日智利8.1级地震同震效应分钟值曲线[图3(a)，图4]；②仪器标定：2014年4月30日标定仪器日分钟值曲线[图3(b)，图5]。数字化仪器精度较高，能记录到同震效应（地震面波）。同震效应是影响数据分析的干扰，需要进行识别和排除。由图4近似部分可见，数据经过分解，同震波被消除，显示出原始曲线变化趋势，从细节部分可以提取同震波。可见，小波变换对同震效应的识别、提取及消除均具有良好效果。经过分解，将2014年4月30日人为标定脉冲干扰去除，反映了原始数据的变化趋势，细节部分也提取到标定干扰信息，并可见具体时间。由图3—图5可知，干扰、脉冲标定和地震同震记录经6层分离基本消失，6阶曲线较平滑，分离效果较好。

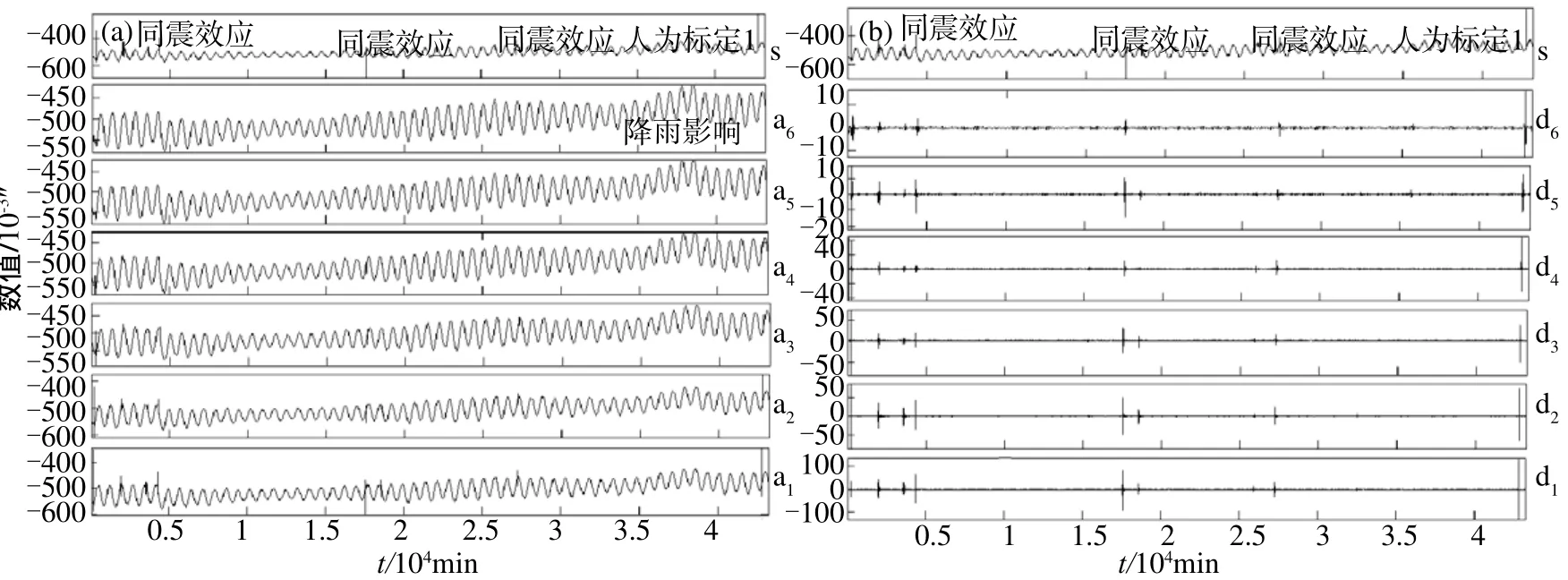
图3 2014年4月倾斜仪北南向数据小波分解（a）近似部分；（b）细节部分Fig.3 Inclinometer NS direction data wavelet decomposition in April, 2014

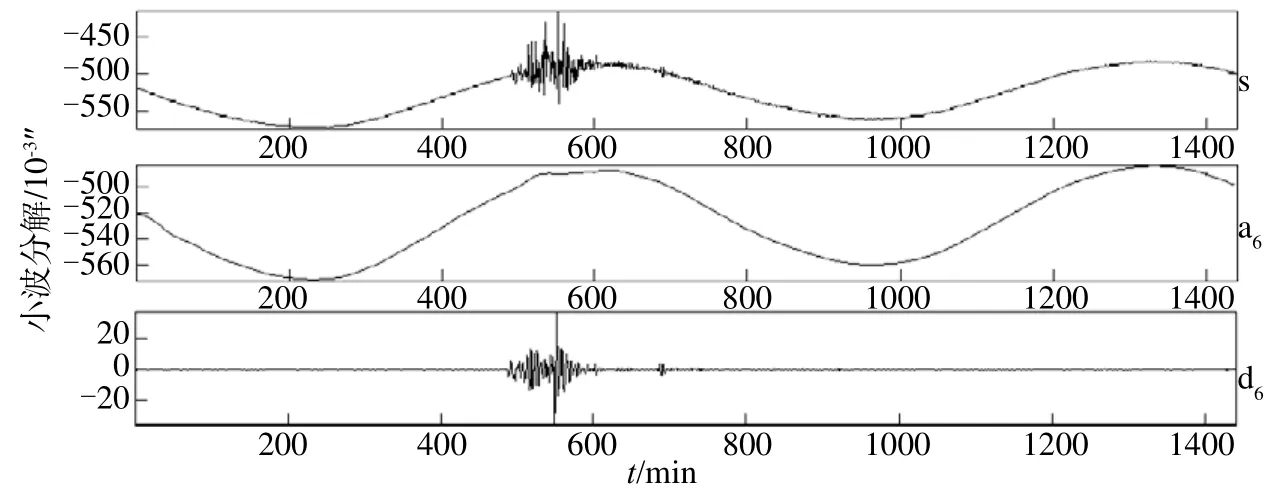
图4 2014年4月2日同震效应的小波分解Fig.4 Wavelet decomposition for coseismic effects on April 2, 2014

图5 2014年4月30日仪器标定的小波分解Fig.5 Wavelet decomposition for instrument calibration on April 30, 2014

2.3 地震前兆异常

以2013年5月18日06∶02∶23黄海海域(37.7°N， 124.7°E)M5.1地震（震中距210 km）为例，分析地震前兆异常。采用多种常规方法，对2013年5月倾斜仪北南向和东西向数据进行分析，发现从2013年5月15日开始出现趋势异常。对2013年5月整点值数据进行小波变换，得到6阶近似部分与细节部分（图6）。由图6可见，自2013年5月15日开始，数据出现趋势异常变化，5月18日发生黄海海域M5.1地震。可见，应用小波分析方法，可对地震趋势异常与短期异常进行有效识别。

图6 2013年5月1日—31日数据小波分解Fig.6 Wavelet decomposition for the data from May 1 to 31, 2013

3 结束语

通过小波分析方法在荣成台形变观测数据处理的应用，验证该信号处理方法对于数据波动、仪器标定、同震效应及不同频率信息的识别、分离具有较好效果，一些地震短临变化也能清晰突显，使各种长短期震前异常识别变得容易，有利于利用地震前兆数据进行地震预测。威海地区可以尝试采用小波分析方法进行地震数据处理，并可以推广到其他地震前兆观测项及地震台。

李杰，刘希强，李红，等.利用小波变换方法分析形变观测资料的正常背景变化特征[J].地震学报，2005，27（1）：33-41.

李艳，高振强，冯建琴，等.临汾地震台体应变观测资料映震能力分析[J].地震地磁观测与研究，2011，32（4）：99-104.

薛志芳，于春颂，李非，等.河北昌黎地震台大地电场数字化观测资料小波分析[J].山西地震，2012，152（4）：22-40.

张燕，吴云，刘永启，等.小波分析在地壳形变资料处理中的应用[J].地震学报，2004，26（Supp）：103-109.

张燕，吴云.2008年汶川地震前的形变异常及机理解释[J].武汉大学学报·信息科学版，2010，35（1）：25-30.

张军，陈宇卫，刘泽民，等.小波分析在前兆数据处理中的应用[J].地震地磁观测与研究，2011，26（2）：99-104.

宋治平，武安绪，王梅，等.小波分析方法在形变数字化资料处理中的应用[J].大地测量与地球动力学，2003，23（4）：21-27.