环锭纺纱气圈顶端张力To的分析
2015-06-01周炳荣
周炳荣
(东华大学,上海 201620)
•技术专论
环锭纺纱气圈顶端张力To的分析
周炳荣
(东华大学,上海 201620)

环锭纺;锭速变化规律;纱张力;控制;气圈
0 引言
在环锭细纱机上气圈顶点o的纱张力是To,假定纱和导纱钩之间摩擦很小,则在导纱钩上方纱张力近似是To。纱张力To因气圈纱高速回转的离心力和筒管卷绕的纱张力共同作用而产生,随气圈高度h和卷绕直径dw大小而变化;由于其大小及变化影响到成纱质量、卷绕紧密、气圈回转稳定、纺纱断头率、机器生产率、锭子功率消耗等,因而应设法调节和控制它,使纺纱工艺在最有利情况下进行。
纱张力To大小及变化只能从气圈理论的分析获得。气圈理论主要是研究气圈纱曲线形状与张力,这两者是相互关联的;准确地说,气圈纱曲线是瞬时纱张力与外力平衡作用的标志。作用在纺纱气圈纱曲线任意质点上外力有离心力、空气阻力、科氏力、纱自重;其中以离心力最大,纱自重最小。为简便计,在计算纱张力To时只考虑离心力作用。过去多位学者论证得出,仅计离心力作用时气圈纱曲线近似于正弦曲线,迄今这仍然是共识。然而纱张力计算就不同了,它须“取钢丝圈为脱离体”做分析得到,这就与钢丝圈—钢领接触型式有关。早在1950年,P.F.格罗申,A.П 拉科夫等认为钢丝圈—钢领为两点接触,得出纱张力Tx计算式,如本文式(f1)[1-2]。现在已认识到钢丝圈—钢领为一点接触,这个公式就不能用了。1996年,我校陈人哲教授在《纺机设计》中提出纱张力Tt计算式[3]是正确的——笔者再次导出,如本文式(f2),以期广泛应用。
笔者经研究认为,C.马克在1956年给出的气圈方程[4]——如本文式(1a)所示是正确和全面的,它计及了离心力、空气阻力、科氏力、纱自重等作用,可用电脑计算和绘出三维的气圈纱曲线形状。为计算纱张力T,笔者补充了气圈张力参数p计算式[5],它适用于钢丝圈—钢领为一点接触情况;纱张力To=mω2p2,是空间力。然而,从这个气圈方程也能导出仅计离心力作用时气圈纱曲线近似为正弦曲线,如本文式(3),其形状由张力参数pz(cm)确定;纱张力To=mω2pp2,在平面xoz内,如图1所示。
1 气圈纱曲线方程式

(1a)
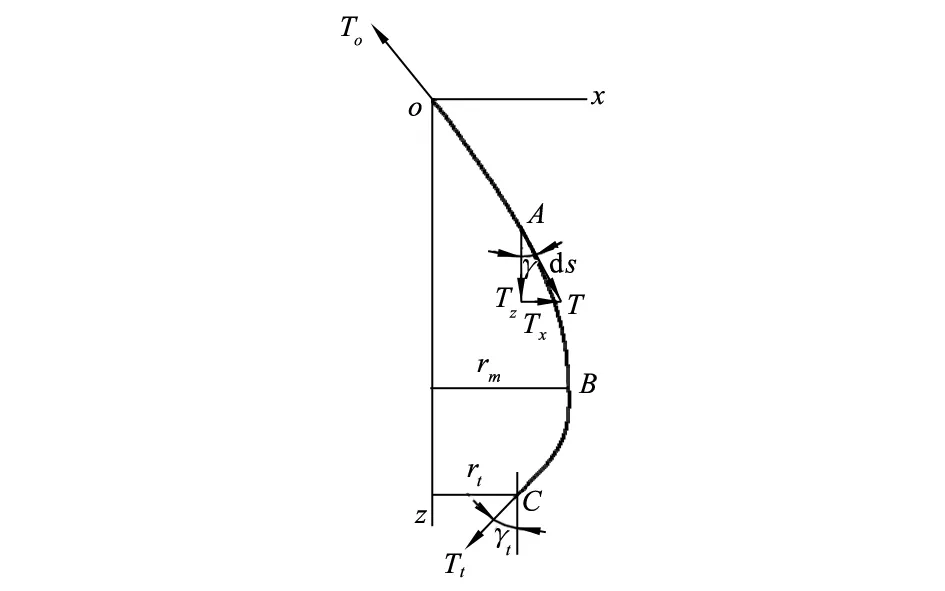
图1 气圈纱曲线为正弦曲线
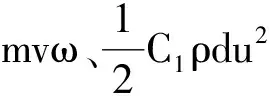
(1)
由图1可知,纱张力T由分量Tx与Tz合成,则有关系T2=Tx2+Tz2,及sinγ=Tx/T;式中:γ为纱曲线切线对于轴z的斜角,故得:
上式积分后得:
(2)
式中:
T——纱曲线上任意点的纱张力;
To——在导纱钩处气圈顶端纱张力;
r——纱曲线上任意点的转动半径;
m——纱的线密度;
ω——气圈纱曲线绕轴z回转的角速度(≅锭速)。
因此,在钢丝圈接触处气圈底端纱张力Tt按式(2a)确定。
(2a)
式中:
rt——在钢丝圈上纱接触点的回转半径。
力To和Tt都在平面xoz内,且To>Tt。接着解式(1)的第一分式,近似取纱微段质量mds≅mdz,则得:
dTx=-mω2xds≅-mω2xdz
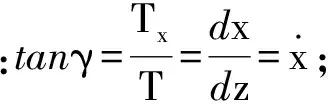

其解是
(3)
式中:
rm——任意常数,及
(3a)
当气圈高度为h时,即z=h,x=rr(钢领半径),则得:
(3b)
式(3)表明,在纱质点的离心力作用下气圈纱曲线近似是一支正弦曲线,位于平面xoz内,最大半径是rm,其定义域为[0,π];纱曲线斜率的通式为:
(4)
令z=0,代入则得气圈纱曲线顶角γo;又令z=h,代入则得气圈纱曲线底角γt;故得:
(4a)
(4b)
纱张力沿着纱曲线的切向,力Tz是它在轴z方向上分量,故有Tz=Tocosγo为定值;此式两端同除以mω2得:
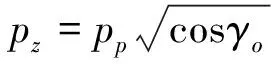
(5)
式中:
(5a)
及
(5b)
称pp为气圈纱曲线(二维的)张力参数;pz为z向张力参数。
2 气圈纱张力T
如上所述,必先给出张力参数pz值才能用式(3)确定纱曲线的形状;然而张力参数pz值的确定又与气圈纱曲线形状(角γo,γt)有关。那怎么解出张力参数pz呢?
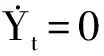
pp2=
0.5rt2=pz2/cosγo
(6)
式中:
cosφ=sinγtcosβ,sinβ=rw/rr
(6a)
M——钢丝圈质量;
rM——钢丝圈质心的转动半径;
μ——钢丝圈与钢领的摩擦因数;
μ1——纱与钢丝圈接触表面的摩擦因数;
φ——纱在钢丝圈截面上接触包围角;
β——纱卷绕角;
rw——纱管卷绕半径(=0.5dw);角γt、γo的计算按式(4a)、(4b),它们与h、pz有关。
将μ、μ1、φ、rM及rt视作常数,式(6)可演算成F(pz,rw,h)=0类型的式子,意即张力参数pz由h、dw确定。就某气圈来说,其气圈高度h及卷绕直径dw值为已知,使用电算二分法,从式(6)可解出这气圈的张力参数pz及pp,相应的纱张力To=mω2pp2。
3 计算实例
例1:国产某型细纱机,纺T/R65/35纱,Tt=18.5tex,锭速14kr/min,钢丝圈6802-5/0,钢领PG1-4554,筒管直径18mm(有锥度),满管直径42mm,钢领板短动程53.23mm,钢领板升降为180mm。
计算参数:μ=0.22,μ1=0.37,M=0.042 1g,rM=2.465cm,m=0.000185g/cm,rr=2.25cm,ω=1 466.075rad/s,rf=4.2cm,筒管半径ro与筒管自身锥度有关,可按其零件图算出,取rt=2.3cm。
图2是本例细纱机气圈高度变化规律图,可获得一落纱期间任意时刻t气圈高度h和卷绕直径dw值,用式(6)算得pz、pp及To见表1。表中字符脚标为“f”者,属于在钢领板短动程下端的参数,而字符脚标为“o”者,属于在钢领板短动程上端的参数。例:df和do表示满管直径和空管直径;Tof表示在钢领板短动程下端的纱张力,Too表示在钢领板短动程上端的纱张力。表1中位置0~6 是纱管的管底期,7~24是管身期,25~34是管顶期。
按表1所载的数据制成纱张力To—t/T曲线图,如图3所示。由图3可知:① 在同一个t/T位置上曲线Too在上而Tof在下,说明一落纱期间钢领板在短动程顶端时纱张力Too大于在短动程底端纱张力Tof;也说明卷绕直径小,气圈高度小的情况气圈纱张力To大;② 一落纱期间纱张力Too的变化呈上升(而不是下降)趋势,大纱时达到最大;③ 一落纱期间纱张力Tof的变化在始纺时迅速下降,位置5附近达到最小,此后呈上升趋势,在大纱时迅速增长达到最大;④ 因所使用的筒管在形状上有了改进,下部做成有一定锥度的锥台,使始纺时卷绕直径dw较大,故小纱期间纱张力Too、Tof降低。
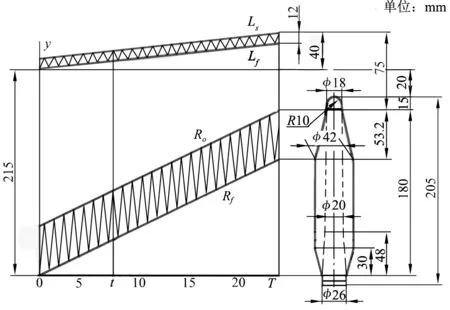
图2 某细纱机气圈高度h的变化规律

表1 纱张力Tof及Too
4 转数可变的锭子
在环锭细纱机上应用转数可变的锭子主要是希望降低过高的纱张力而把较低的纱张力提升到平均值;使导纱钩至前罗拉钳口之间的纱线保持一个均匀稳定的张力,以期提高成纱质量,降低纺纱断头和提高机器生产率,这里最主要的要求是纱张力To为定值。
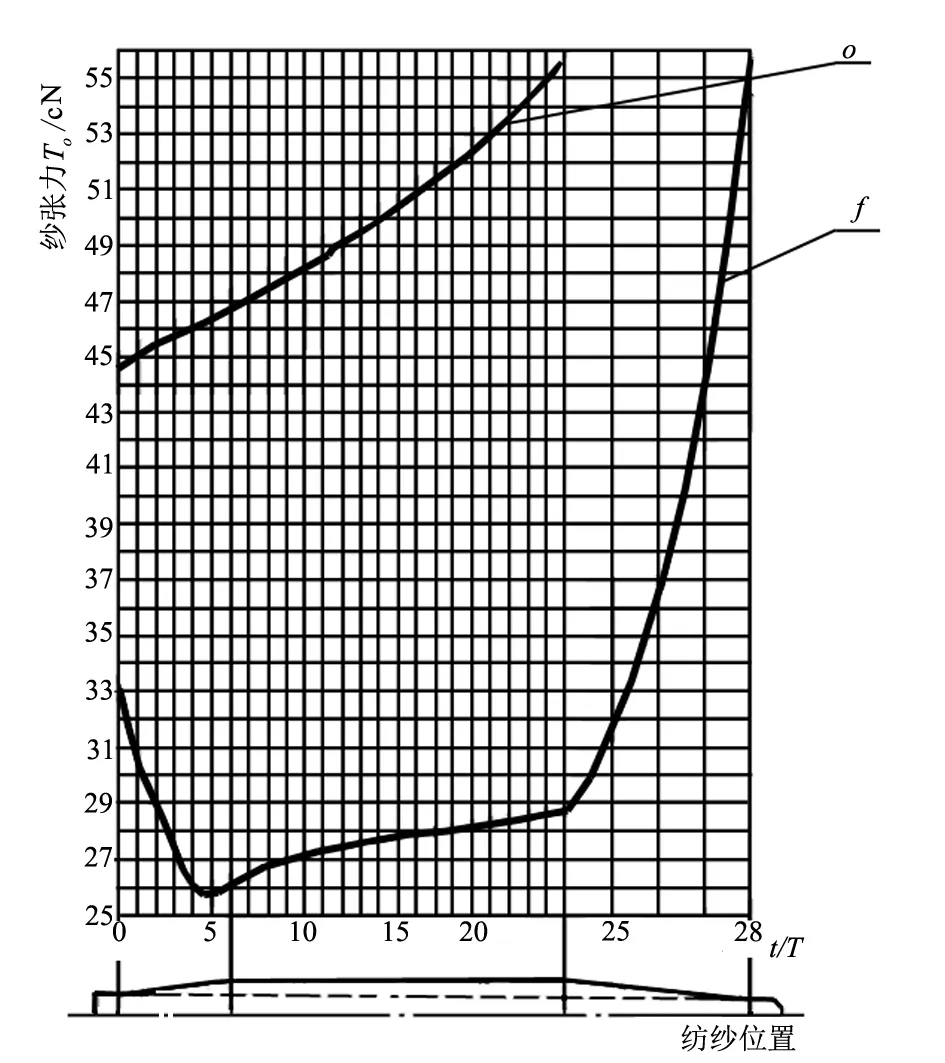
图3 一落纱期间纱张力To的变化
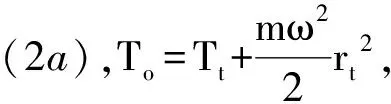
4.1 锭速基本调节规律
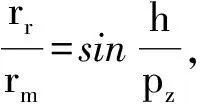
(7)
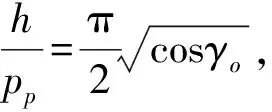
(7a)
按表1结果,cosγo值为0.93~0.98,今取cosγo=0.95,则得:
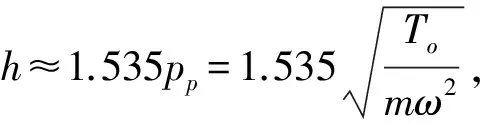
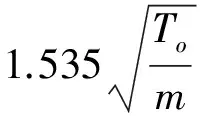
(8)
式(8)展示了参数h、ω、To、m之间的关系。对于锭速ω不变的细纱机,始纺时气圈高度为最大值hm,则乘积hmω也最大;若采用式(8)确定所纺纱号m的纱张力To值也是最大,再大的纺纱张力是做不到的;所以乘积hmω标志着这台细纱机的纺纱能力,这参数也正是纺纱工艺和纺机设计者感兴趣的。
若要求一落纱期间纱张力To为定值,则锭速ω须与气圈高度h成反比例变化,即:
hω=定值
(8a)
4.2 锭速逐层调节规律
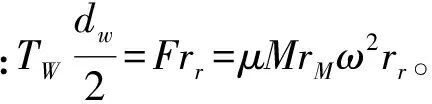
又气圈底端纱张力Tt=TW/exp(μ1φ)=2μMrMω2rr/dwexp(μ1φ)=kt/dw(因此,常数kt内含因数ω2),将它代入式(2a)则得下式:

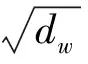
(9)
上列式中kt、kp、k均为常数。
例2:承上例,今取纱张力To=33.34cN,这是位置o时Tof值,此时h=21.5cm,dw=2.6cm,按式(8)算得ωh=0.958 5×103rad/s。此后气圈高度h减小,按式(8a)计算得到ωh值,见表2 。在位置20以后气圈最大半径不能看到,式(8a)失效,不适用。
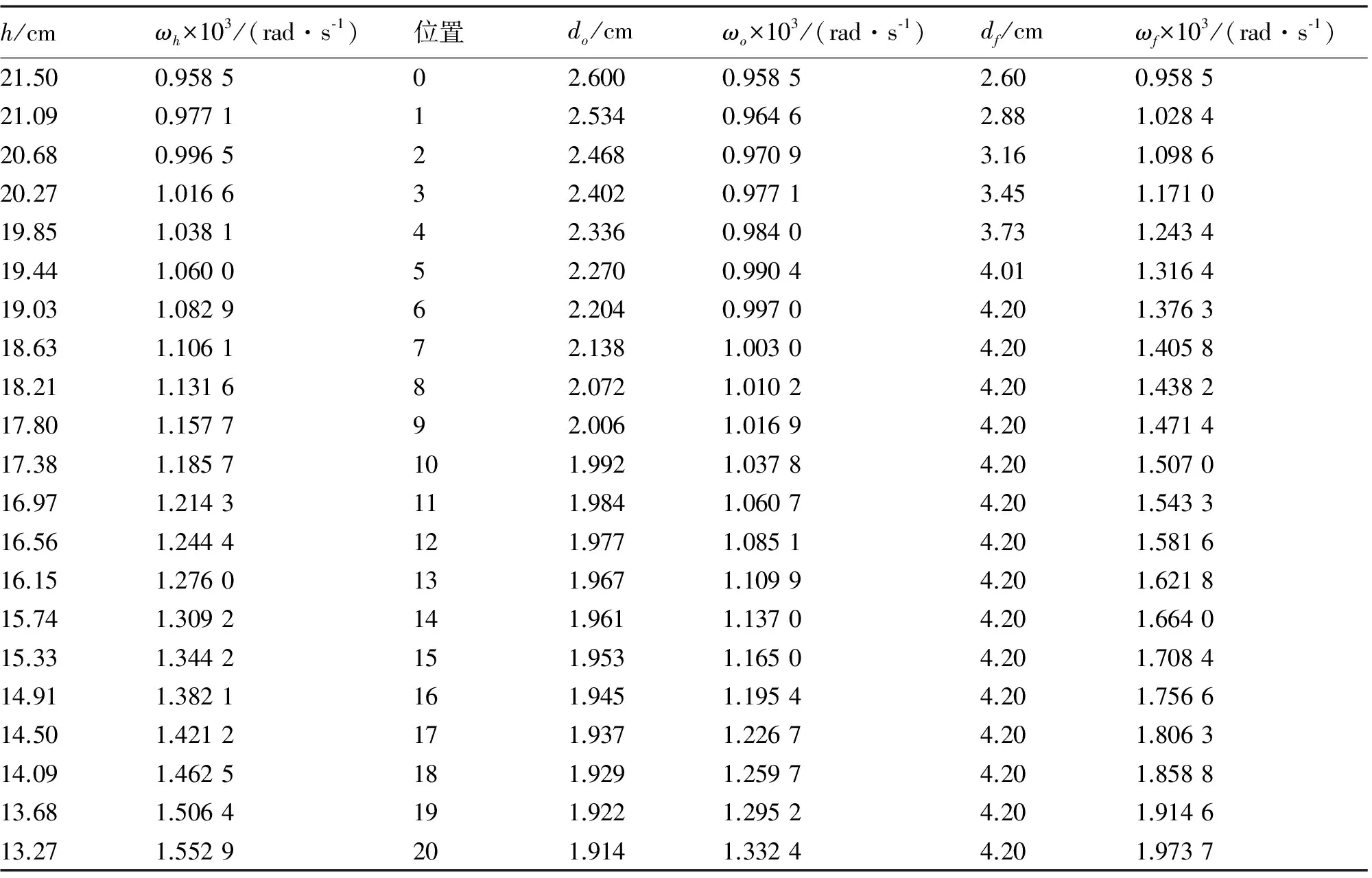
表2 锭速ωh、ωo及ωf

根据表2的数据绘出图4。图中曲线oabcd为基本调速曲线 (图中线段bcd系自行拟订),然后在位置0~20各根纵线上划定逐层调速区间,最后勾划出上、下两根虚线,形成调速区间的界线,这样就制成锭速变化曲线图。它所表达的是在维持纱张力To=33.34 cN情况下锭速ω变化规律。
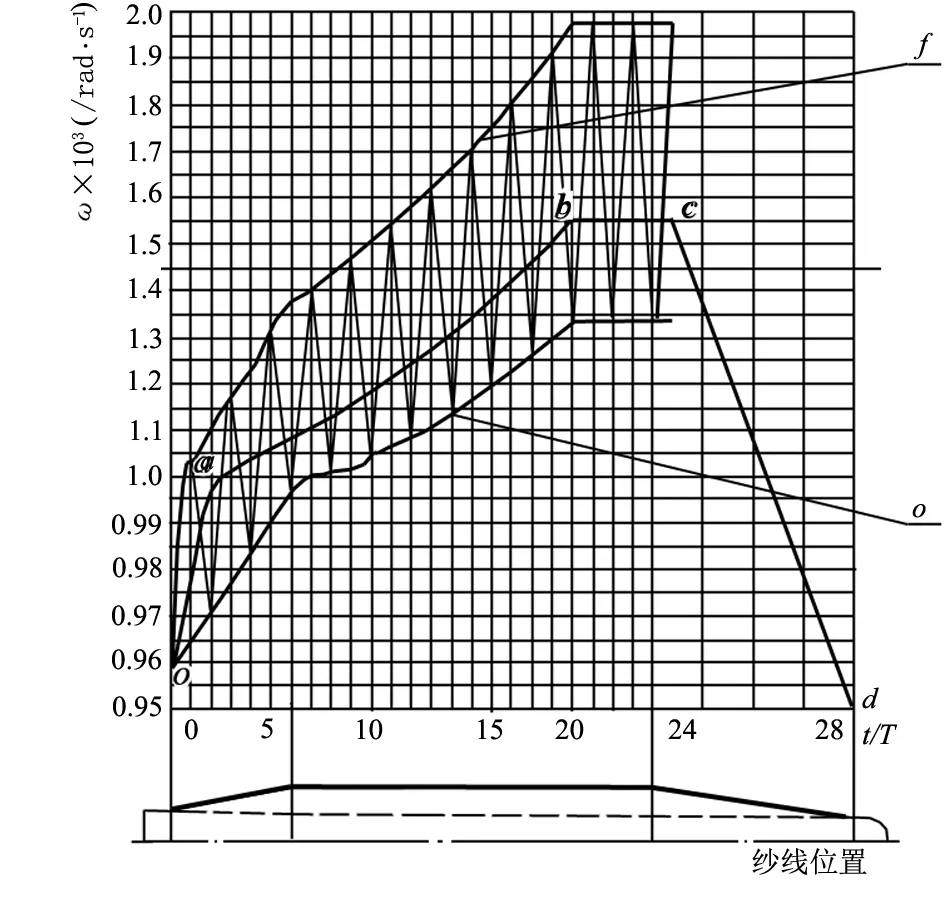
图4 锭子变速曲线
本例原定锭速ωst=1 466.075 rad/s恒定,现改为锭速可变的,以完成纺纱张力To=33.34 cN为定值的要求,从图4的结果来看,在卷绕小直径do时锭速ωo降低了,并且始终是ωo<ωst;卷绕大直径df时锭速ωf提升了,虽然ωf>ωst占有位置一半左右(10~24);但总的来说,细纱机产量较原来下降。
5 结论
5.1 仅计离心力作用时气圈纱曲线近似是正弦曲线,在平面xoz上,定义域[0,π],气圈张力参数pp由式(6)确定之,纱张力To=mω2pp2。
5.2 实例计算的结果表明,由于现用的筒管底部直径放大,做管底时纱张力To降低了;但在做管身时纱张力To逐渐增大,以至于做管顶时纱张力To增至最大。
5.3 在环锭细纱机上应用转数可变的锭子主要要求纱张力To恒定,降低过高的纺纱张力,把较低的纺纱张力提升到平均值。这个纱张力To似以始纺时纱张力Tof为宜。
5.4 锭速ω所采取的变化规律有:① 基本调节,锭速ω随着气圈高度h连续地减小而增大,两者成反比例变化,如式(8a)示;② 逐层调节,当气圈高度h为某值时,锭速ω随着卷绕直径dw增大而增大,如式(9)示。如要求纱张力To为定值,则二者必须兼有,如图4曲线所示。
5.5 过去曾使用锥轮无级变速器完成锭速阶段调节,现在使用的筒管底部直径放大,已降低了小纱期间纱张力Too、Tof;但是若要降低大纱期间纱张力Tof、Too,只有选择锭速可变的途径了。
5.6 从锭子变速曲线(图4)可以看出,改为锭速可变的细纱机后细纱产量有所降低。
6 附录
6.1 关于文献 “balloon control”
文献balloon control(P.F.Grishin 著)过去曾在国内部分地区受到注意,今指出它的不足和错误之处,防止谬以千里。
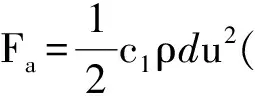

c) 他认为“钢丝圈—钢领是离散的多点接触,这比取钢丝圈—钢领单点接触计算摩擦更为真切”,故他在文中取钢丝圈—钢领的摩擦力为F=fNx+fNy,得出纱张力Tx计算式如下:
(f1)
式中:
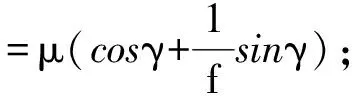
FC=5.6GDn2。
这个说法也出现在前苏联的拉科夫著《精纺工程》里(参见文献[2])。现代钢丝圈与钢领已改进为一点接触,式(f1)不适用。
6.2 纱张力Tt
如上所述,仅计离心力作用时气圈纱曲线近似是正弦曲线,它在平面xoz内;纱张力T沿着纱曲线切向作用,则气圈顶端张力To和气圈底端张力Tt都在平面xoz内;但卷绕张力Tw在平面xoy内,并有关系Tw=Ttexp(μ1φ)。
今取钢丝圈为脱离体,作用在钢丝圈上力有:① 钢丝圈离心力FM,FM=MrMω2;② 气圈底端纱张力Tt,卷绕纱张力Tw;③ 钢领接触面上反作用力N及钢丝圈与钢领之间摩擦力F,F=μN;以上诸力互为平衡,则组成一个空间的封闭的多边形,如图5所示,于是得出下式:
∑x=0,即FM+Ttsinγt-Twcosβ-Nx=0;
∑y=0,Twsinβ-μN=0;
∑z=0,-Ttcosγt+Nz=0。

图5 钢丝圈受力分析
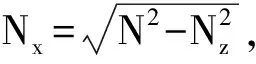
(f2)
联立式(2a)、(f2)及应用式(5a)也能得到式(6)。
[1] Grishin P.F.Balloon control[J].Platts-Bulletin,1954,8(6):8.
[2] А.П 拉科夫.精纺工程[M].北京:纺织工业出版社,1952:82-83.
[3] 陈人哲.纺织机械设计原理:上[M].2版.北京:中国纺织出版社,1996:303-304.
[4] DE BARR A.E.The principles and theory of ring spinning[M].London:The Textile Institute,1965.
[5] 周炳荣.纺纱气圈理论[M].上海:东华大学出版社,2010.
Analysis of Yarn TensionToon the Balloon Top in the Ring Spinning Process
ZHOU Bingrong
(Donghua University,Shanghai 201620,China)
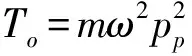
ring-spinning process;the law of spindle speed variation;yarn tension;control;balloon
2014-11-11
周炳荣(1934—),男,东华大学教授。
TS103.11+5
A
1001-9634(2015)03-0001-07
