三相三线电路中的多端电路瞬时功率理论推导

杨秀川，田铭兴

(1．国网宁夏电力公司培训中心，宁夏 银川750001; 2．兰州交通大学自动化与电气工程学院，甘肃 兰州730070)

三相三线电路中的多端电路瞬时功率理论推导

杨秀川1，田铭兴2

(1．国网宁夏电力公司培训中心，宁夏 银川750001; 2．兰州交通大学自动化与电气工程学院，甘肃 兰州730070)

针对在电压电流畸变情况下基于相电压定义的传统功率理论已失去其有效性的问题，提出了多端电路的理念。将三相三线制电路作为三端电路处理，给出了端电压和端电流的定义。并且利用瞬时端电压和瞬时端电流定义了瞬时有功和无功功率。文中分别在电压电流均正弦对称、电压正弦对称电流畸变不对称以及电压电流均畸变不对称三种情况下推导了在三端电路中瞬时有功功率和瞬时无功功率的表达式，该表达式与基于瞬时功率理论推导得出的表达式一致。据此给出了三端电路中瞬时有功功率和瞬时无功功率的定义。

多端电路;三端电路;畸变不对称;瞬时功率

1 引言

目前，不论是三相电路还是多相电路，其功率计算都是基于“相电压”的，这使得在三相三线系统等类似情况下的相电压的定义和测量出现困难。在正弦对称情况下，相电压可以根据其与线电压的关系计算得到;但是随着电力电子器件的不断使用，以及大量非线性不对称负载接入供电系统，使得电压电流畸变不对称［1，2］，这时正弦对称情况下相电压和线电压之间的关系不复存在，所以因正弦电路而定义的“相”的概念已不适合含有混合补偿设备的电路系统，而多端电路较多相电路而言具有更大的概念外延，因此将多相电路功率理论推广并改进到多端电路应是一项很有意义的工作。

顾名思义，多端电路即为含有多个引出端的电路，其可以作如下定义:如图1所示，在任意一个电路网络中，不论它多么复杂都可以将其主体看成一个黑盒子，黑盒子外的输入端和输出端统称为这个网络的引出端。若引出端的数目为n则称这个电路为n端电路，因为在交流电路的所有形式中，相数最少的单相电路实际上也是由两个引出端构成，所以在n端电路系统中n是大于等于2的，在n大于等于3时则称这个电路为多端电路。

图1 多端电路的一般形式示意图Fig．1 Schematic diagram of general form of multi-terminal circuit

在本文中将三相三线制电路系统看作三端电路进行处理，选择三端中的任意一端作为参考端，在实际应用中可以通过并联电压表方便地测出其他两端到参考端的电压，本文中称之为端电压，也可以通过串联电流表测量得出每个端子上的电流，本文称为端电流。在下文中，分别在电压电流均正弦对称、电压正弦对称电流畸变不对称、电压电流均不对称三种情形下，推导通过瞬时端电压和瞬时端电流定义瞬时有功功率、瞬时无功功率的表达式。结果表明，利用瞬时端电压和瞬时端电流定义瞬时功率是可行的，并且端电压和端电流的定义物理意义更加明确，在实际应用中测量更加简洁、方便。

2 电压电流均正弦对称情况下瞬时功率定义

文献［3］中提出瞬时有功功率等于瞬时电压和瞬时电流的乘积(点积)，见式(1);瞬时无功功率等于瞬时电压和瞬时电流的叉积，见式(2):

瞬时电流向量i可以分解为两个正交的分量之和，该分量分别为瞬时有功向量 ip和瞬时无功向量iq，见式(3):

由于瞬时电压向量和瞬时无功电流向量正交，所以u·iq=0，而瞬时电压向量和瞬时有功电流向量在一条直线上，所以u×ip=0。因此，瞬时有功功率就可以等于瞬时电压和瞬时有功电流的点积，见式(4);瞬时无功功率等于瞬时电压和瞬时无功电流的叉积，见式(5)。

三相三线制电路对应多端电路示意图如图2所示，图中将负载端看成一个黑盒子，三相三线电路有三个出线端，可看作三端电路。由于在三相三线系统中负载是由三相发电机供电或者由发电机发出经由变压器变压后供电，而三相发电机或者变压器是存在中性点的，如图2中 N点，假设三个端子间也存在一点N1，如图中N1点，该电位点的电位UN1与电源中性点的电位 UN的电位差满足 UNN1=UNUN1=0，那么称该点为虚拟中心点，相电压即定义为各个端子到虚拟中性点之间的电压。

图2 三相三线制电路对应的三端电路示意图Fig．2 Schematic diagram of three-terminal circuit corresponding to three-phase three-wire circuit

在三相正弦对称系统中，假设线电压的瞬时表达式为:

将线电压的瞬时表达式写成相量形式为:

如图2所示，在三相正弦对称系统中，相电压可以直接根据其与线电压的关系得到［1］:

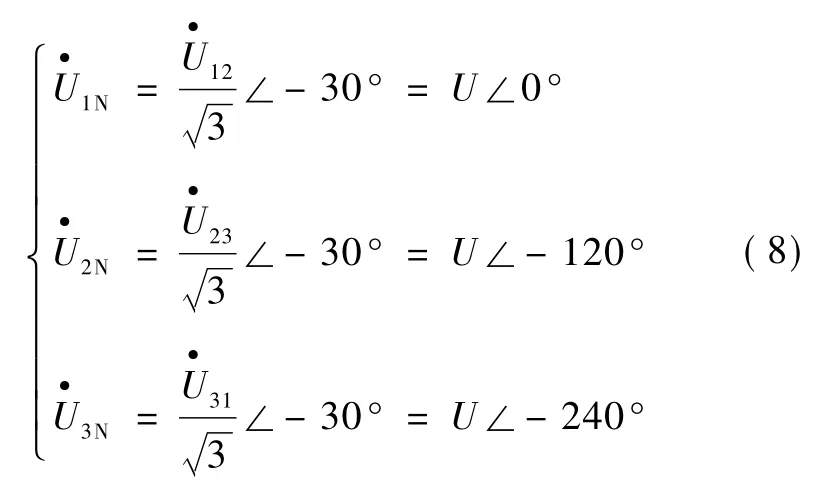
将相电压的相量形式转化为瞬时表达式:

假设端电流的瞬时表达式为:

式中，φ为电压和电流的相位差。

端电流可以分解为有功端电流和无功端电流，其瞬时表达式分别为:

在多端电路系统中，可以利用选择任意端作为参考端后的端电压和端电流来定义其功率，例如选择3端作为参考端，电路示意图如图3所示。其端电压的瞬时表达式为:

图3 选择3端作为参考端时的三端电路示意图Fig．3 Schematic diagram of three-terminal circuit when choosing terminal 3 as reference terminal

根据式(4)，图3所示三端电路的瞬时有功功率可由各个端子上的瞬时端电压和瞬时有功端电流取点积后求和得到，将式(13)和式(11)代入式(14)中可得:

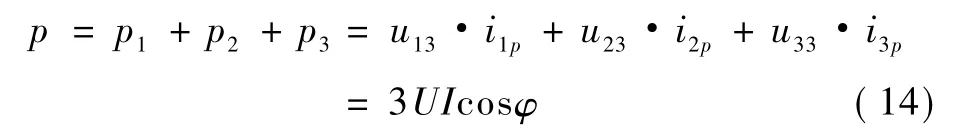
根据式(5)，图3所示三端电路的瞬时无功功率可由各个端子上的瞬时端电压和瞬时无功端电流取叉积后求和得到，将式(13)和式(12)代入式(15)中可得:

将瞬时无功端电流旋转90°即可将式(15)中的叉积转变为点积:

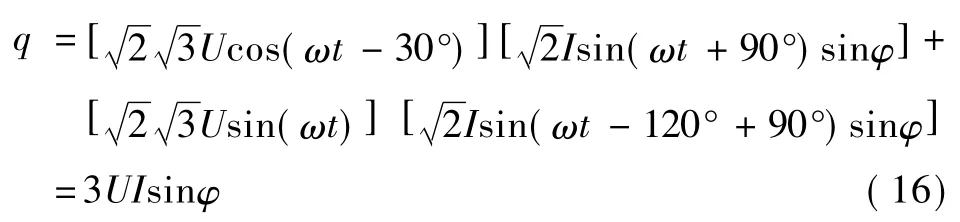
推导得出利用瞬时端电压和瞬时端电流定义的瞬时有功功率和无功功率表达式与文献［4］中用相电压和相电流定义的瞬时有功功率和无功功率表达式相同，但是端电压的物理意义更加明确且在实际应用中更好测量。

3 非正弦不对称系统

3.1 电压为正弦对称电流为畸变不对称时

在电力系统中，通常存在电源电压正弦对称，而电流由于非线性负载以及电力电子器件的使用造成的畸变或不对称现象［5］，下面推导电压为正弦对称、电流为畸变不对称情况下的三端电路的瞬时功率的表达式。

由于电压为正弦对称，所以其瞬时表达式可以表示为:

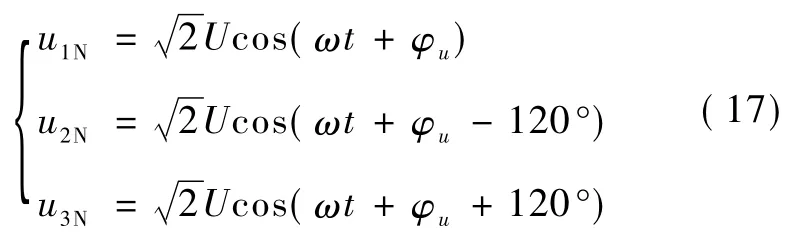
对于电力系统中的非线性问题，由于电压和电流具有周期性畸变的特点，可以将周期性畸变的电压和电流转化为非正弦周期电流电路处理(在后面的问题研究中都是根据此特性确定瞬时量的表达式)［4］，并且在三相三线制系统中只存在正序、负序，不存在零序电流，所以端电流瞬时表达式可以表示为:

设1、2、3三个端子上的第 ki次谐波电流 i1ki、i2ki、i3ki的瞬时表达式为:

将端电流分解为有功端电流和无功端电流后，其瞬时表达式分别为:

如图2所示，当选择3端作为参考端时，各个端子上的端电压的瞬时表达式为:

根据式(4)，该三端电路第 ki次谐波电流的瞬时有功功率可以利用各个端子上瞬时端电压和瞬时有功端电流取点积后求和确定，将式(22)和式(20)代入式(23)中得:

根据式(5)，该三端电路第 ki次谐波电流的瞬时无功功率则可利用各个端子上瞬时端电压和瞬时端无功电流取叉积后求和确定，采用与式(16)相同的方法，把瞬时无功电流旋转90°将叉积运算转化为点积运算，将式(22)和式(21)代入式(24)中得:

根据上述推导可以得出，在电压正弦对称电流畸变不对称时，该三端电路系统的瞬时有功功率为:

瞬时无功功率为:

3.2 电压电流都为畸变不对称时

在电压正弦对称情况下，电源电压是正弦对称的，三相电源电压 e'1+e'2+e'3=0;由于虚拟中性点电位UN1与电源中性点电位UN之间的电位差为0，所以三端相电压之和也为0，且可以通过线电压和相电压之间的关系来确定相电压。而在非正弦不对称情况下，不但不满足正弦对称情况下线电压和相电压之间的关系，而且三相电源电压之和也不为0。这就表明由不同的三相电动势可得到相同的线电压，但是由线电压则无法唯一确定相电压，也就是说在非正弦不对称情况下，对负载起决定作用的是线电压而不再是三相电动势本身。文献［6］中指出在任意的三相三线电路中总可找到一组三相电动势e1、e2、e3满足三相之和为0，用其去替代原三相之和不为0的e'1、e'2、e'3，并利用对称分量法将某特定 m次谐波分解为正序、负序、零序。由于三相正序、负序相加为0，而三相零序相加为，所以采用一组去除了零序分量的电动势去代替原电动势，见式(27):

式中，e1+e2+e3=0。

由第2节中提到的相电压的定义可知，因为虚拟中性点的电位与电源中性点电位的电位差为零，而且在选择任意端作为参考端时定义的端电压中同样也不反映零序向量，所以三端的相电压也可以采用 u1N=e1、u2N=e2、u3N=e3来代替原来的三端上的电压u'1N、u'2N、u'3N。也正因为有此特点，所以三端上的相电压可以利用式(28)来确定:

根据上述原理采用一组去除了零序分量的电动势代替原电动势，三端上的电压只剩下正序和负序分量，因此其瞬时表达式可以表示为:

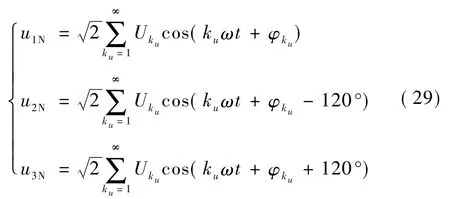
设1、2、3三个端子上的第 ku次谐波电压 u1ku、u2ku、u3ku的瞬时表达式为:

各个端子上的端电流的瞬时表达式与式(18)相同，而1、2、3三个端子上的第 ki次谐波电流 i1ki、i2ki、i3ki的表达式与式(19)相同。因此将第 ki次谐波端电流 i1ki、i2ki、i3ki分解为有功端电流 i1kip、i2kip、i3kip和无功端电流 i1kiq、i2kiq、i3kiq，其瞬时表达式分别为:

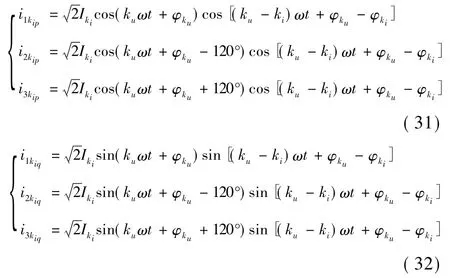
当选择3端作为参考端时，其各个端子上第 ku次谐波的端电压的瞬时表达式可以表示为:

根据式(4)，该三端电路第 ki次谐波电流和第ku次谐波电压的瞬时有功功率可以利用瞬时端电压和瞬时有功端电流取点积后求和得到，将式(33)和式(31)代入式(34)中得:

根据式(5)，该三端电路第 ki次谐波电流和第ku次谐波电压的瞬时无功功率可以利用瞬时端电压和瞬时端无功电流取叉积后求和得到，采用与式(16)相同的方法，把瞬时无功电流旋转90°将叉积运算转化为点积运算，将式(33)和式(32)代入式(35)中得:

根据上述推导可以得出，在电压和电流均畸变不对称时，该三端电路系统的瞬时有功功率为:

该三端电路系统的瞬时无功功率为:

通过以上推导可以得出，利用瞬时端电压和瞬时端电流推导得出的瞬时有功功率和瞬时无功功率的表达式与文献［7］中基于瞬时功率理论推导得到的表达式相同。但是在电压电流畸变的情况下，由于相电压的定义和测量都十分困难，而端电压和端电流的物理意义明确且测量简便。因此在三端电路中可以给出以下定义。

(1)定义1:瞬时有功功率等于选择任意一端作为参考端时，各个端子上相对于参考端的瞬时端电压与瞬时端电流取点积后求和。

(2)定义2:瞬时无功功率等于选择任意一端作为参考端时，各个端子上相对于参考端的瞬时端电压与瞬时端电流取叉积后求和。

本文在电压电流均正弦对称、电压正弦对称电流畸变不对称以及电压电流均畸变不对称三种情况下，都是选择3端作为参考端对端电压和端电流进行定义，进而推导得出瞬时有功功率和瞬时无功功率的表达式，同理，选择其他任意一端作为参考端可以得出同样的结果。

4 结论

(1)本文分析了现有功率理论在电压电流畸变不对称情况下的缺陷，并提出利用多端电路的理念将三相三线制电路看成一个三端电路处理的观点。

(2)文中给出了端电压和端电流的定义，并将瞬时端电流分解为两个正交的瞬时有功端电流和瞬时无功端电流。在电压电流均正弦对称、电压正弦对称电流畸变不对称以及电压电流均畸变不对称三种情况下，利用瞬时端电压和瞬时端电流推导瞬时有功功率和瞬时无功功率的表达式。推导结果与文献［7］中基于瞬时无功功率理论推导出的结果一致。

(3)最后根据推导结果给出了在三端电路中瞬时有功功率和瞬时无功功率的定义，在此定义中所用到的端电压的概念较相电压具有更大的概念外延，且物理意义更加明确，测量无需中间计算环节，更加简便。

［1］邱关源 (Qiu Guanyuan)．电路 (Circuit)［M］．北京:高等教育出版社 (Beijing:Higher Education Press)，2007.303-305．

［2］赤木泰文 (Hirofumi Akagi)．瞬时功率理论及其在电力调节中的应用 (Instantaneous power theory and application to power conditioning)［M］．徐政 (Xu Zheng)译．北京:机械工业出版社 (Beijing:China Machine Press)，2009.17-30．

［3］ 戴先中，唐统一，孙树勤 (Dai Xianzhong，Tang Tongyi，Sun Shuqin)．非正弦三相电路中瞬时无功量的普遍化定义 (A generalized definition of instantaneous reactive quantity in nonsinusoidal three-phase systems)［J］．中国电机工程学报 (Proceedings of the CSEE)，1998，18(6):388-394．

［4］熊元新，陈允平 (Xiong Yuanxin，Chen Yunping)．正弦电路瞬时功率理论研究 (Study on theory ofinstantaneous power of sinusoidal circuit)［J］．电网技术 (Power System Technology)，2001，20(6):18-20．

［5］Xianzhong Dai，Guohai Liu，Ralf Gretsch．Generalized theory of instantaneous reactive quantity for multiphase power system［J］．IEEE Transactions on Power Delivery，2004，19(3):965-972．

［6］王勤，戴先中 (Wang Qin，Dai Xianzhong)．非正弦不对称三相三线电路负载侧相电压的定义与测量 (The definition and measurement load’s phase voltages in nonsinusoidal unsymmetrical 3-phase 3-wire system)［J］．电工技术学报 (Transactions of China Electrotechnical Society)，1997，12(6):55-58．

［7］刘进军，王兆安 (Liu Jinjun，Wang Zhao’an)．瞬时无功功率与传统功率理论的统一数学描述及物理意义(Uniform mathematic description of instantaneous reactive power theory and conventional power theory and its physical meaning)［J］．电工技术学报 (Transactions of China Electrotechnical Society)，1998，13(6):6-12．

Deduction of instantaneous power theory of multi-terminal circuit in three-phase three-wire circuit

YANG Xiu-chuan，TIAN Ming-xing
(1．State Grid Ningxia Electric Power Training Centre，Yinchuan 750001，China; 2．School of Automation＆Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

In view of the traditional power theory based on the definition of phase voltage is no longer valid under the circumstance of distorted voltage and current，the concept of multi-terminal circuit is proposed．Take the threephase three-wire circuit as an example，which is treated as the three-terminal circuit．Definitions of its terminal voltage and current are proposed in this paper while the instantaneous active power and reactive power are defined using instantaneous terminal voltage and current．The expressions of instantaneous active power and reactive power are deduced under three conditions respectively，which both the current and voltage are sinusoidal and symmetric，the voltage is sinusoidal and symmetrical while the current is distorted and asymmetric and both the current and voltage are distorted and asymmetric．The results of them are the same as the expressions deduced under the instantaneous power theory．According to this，the definitions of instantaneous active power and instantaneous reactive power of three-terminal circuit are given．

multi-terminal circuit;three-terminal circuit;distorted and asymmetric;instantaneous power

TM132

:A

:1003-3076(2015)12-0031-06

2014-08-08

国家自然科学基金 (51167009;51367010)、甘肃省科技计划 (1304WCGA181)、兰州市科技计划(2013-4-111)资助项目

杨秀川 (1989-)，男，宁夏籍，硕士研究生，研究方向为功率理论以及谐波抑制与无功补偿;田铭兴 (1968-)，男，甘肃籍，教授，博士生导师，博士，研究方向为电力系统电能质量分析及其综合治理、电力电子技术及其应用、电机电器及其控制。