构架弹性振动对疲劳寿命影响研究*

张 丽，任尊松，孙守光，杨 光

(北京交通大学 机械与电子控制工程学院，北京100044)

构架弹性振动对疲劳寿命影响研究*

张 丽，任尊松，孙守光，杨 光

(北京交通大学 机械与电子控制工程学院，北京100044)

近年来国内地铁车辆转向架构架多次发生弹性振动问题，弹性振动对构架疲劳寿命的影响已引起高度关注。现对国内某型地铁车辆转向架构架动应力进行测试并对数据进行时域和频域分析，得到了构架上发生弹性振动测点的动应力特点;在建立构架有限元模型的基础上，计算了构架自由振动频率，结果表明构架实际线路运用中弹性振动频率与其某阶固有频率一致;对测试数据采用去除振动主频率的方法，得到去除弹性振动后测点的动应力时间历程及分布特性，结合雨流计数法、S－N曲线并应用Miner线性疲劳累计损伤理论，得到发生弹性振动和去除弹性振动情况下构架上不同部位测点的等效应力幅值及疲劳寿命，进而获得构架弹性振动对疲劳寿命影响特性。研究结果表明，发生弹性振动后，构架局部位置疲劳寿命将大幅下降，可降至原设计寿命的1/3。

构架;动应力;弹性振动;疲劳寿命;影响

转向架构架是地铁车辆最重要的承载部件之一，它不仅是转向架两级悬挂系统和牵引制动系统的安装基础，而且起着支撑车体、承受并传递车体和轮对之间各种载荷的作用。随着地铁车辆运行速度提高以及运用一段时间后轨道状态恶化，轮轨系统激扰频率发生改变，致使构架某些部位产生明显的弹性振动，导致这些部位过早产生疲劳裂纹甚至断裂，严重影响构架的疲劳寿命和列车运用安全。这些部位主要包括电机吊座、齿轮箱吊座、构架横侧梁连接处、ATP天线梁等。有鉴于此，开展构架高频弹性振动及其对疲劳寿命影响方面的研究工作是十分必要的。

目前，在构架弹性振动以及疲劳寿命计算和预测方面，已有研究人员对其进行了探索和研究。刘晓雪［1］和贾倩［2］分别根据有限元仿真动应力结果和实测动应力结果，在动应力编谱后对构架疲劳寿命进行了预测和评估;任尊松［3］对构架弹性化处理后，研究了构架弹性振动，数值计算了构架动态应力，获得了车辆直线运行、曲线及某型道岔通过时构架的动态应力分布，为构架疲劳寿命的数值计算评估创造了条件;王成国［4］将构架处理为弹性体，通过数值仿真计算，研究分析构架应力分布，并进行了疲劳分析。文献［5］将构架作为弹性体处理，模拟计算了构架的结构振动;文献［6］同样将构架做弹性体处理，通过仿真分析对构架的疲劳寿命进行了预测。文献［7］将构架考虑为弹性体，进行了通过道岔时转向架结构振动和动态应力分析。但是截至目前，构架在运用过程中发生弹性振动后对其疲劳寿命的影响很少涉及。

有鉴于此，拟在测试某型地铁车辆转向架构架关键部位动应力的基础上，获得构架发生弹性振动测点位置和振动频率，采用有限元法确认该频率与构架自由振动频率的一致性;采用滤波方式去除弹性振动对应的动态应力和振动频次，得到发生弹性振动和去除弹性振动后的构架测点等效应力，进而获得弹性振动对构架疲劳寿命影响特性，以期对构架发生弹性振动后的使用寿命进行预测和评估。

1 动应力线路试验及频谱分析

为了研究地铁车辆在服役过程中构架的弹性振动对疲劳寿命的影响，对北京某型地铁车辆转向架构架关键部位进行了动应力测试，构架主要测点分布如图1所示。这些测点主要是在考虑构架结构、工艺特点以及载荷传递方式等因素后确定，主要分布在构架横侧梁连接部、电机吊座、齿轮箱吊座、小纵梁、牵引和制动座以及定位座周围等。线路测试过程中，列车按照运营条件正常运行，最高测试速度约为70 km/h，多次往返后总测试里程约为200 km。为模拟载乘工况，测试过程中车辆装载沙袋且达到正常满载条件。

对测试数据进行时域和频域分析后发现，电机吊座和齿轮箱吊座等部位均发生了一定程度的弹性振动。图2给出了发生弹性振动测点65和未发生弹性振动测点82的动应力时间历程，这两个测点均布置在电机吊座周围。由此可见，测点65的动应力在－33.2～40.5 MPa之间变化;测点82的动应力在－15.7～11.0 MPa之间变化，发生弹性振动的测点的动应力波动幅值显著增大。

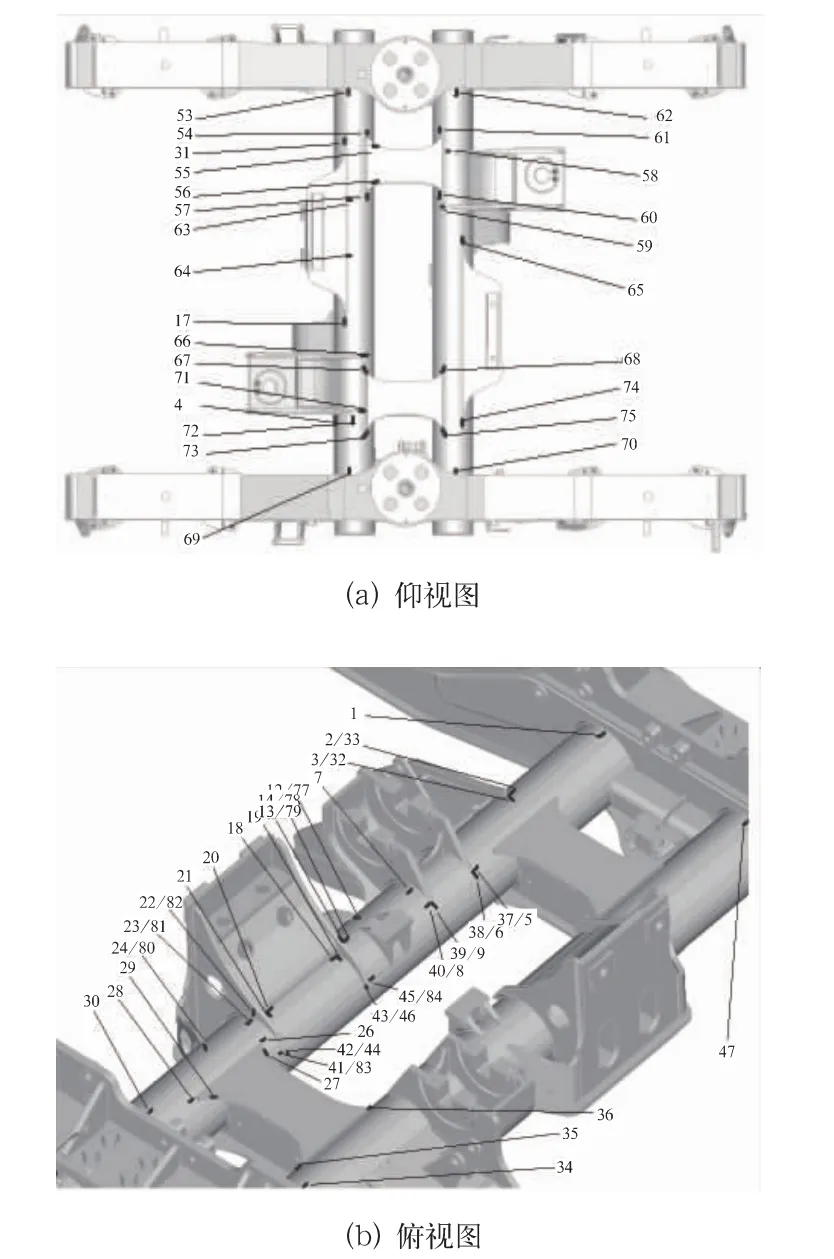
图1 构架测点图

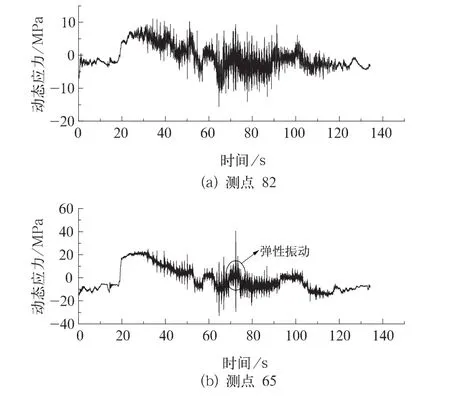
图2 电机吊座周围测点82、65动应力时间历程

为了更加直观地了解发生弹性振动时结构的动应力特征，这里取出图2中圆圈覆盖部分，其弹性振动动应力时间历程如图3所示，由图可见，发生弹性振动时，测点动应力不仅波动幅度大，而且出现频次高。为了通过弹性振动剧烈程度了解弹性振动时的动应力特征，图4给出了该列车ATP天线梁发生弹性振动时测点的动应力时间历程，该测点不仅具有上述65号测点表现出的弹性振动特性，而且其动应力波动幅度更大、振动频次更高，表明ATP天线梁的弹性振动，明显较电机吊座周围的弹性振动剧烈。

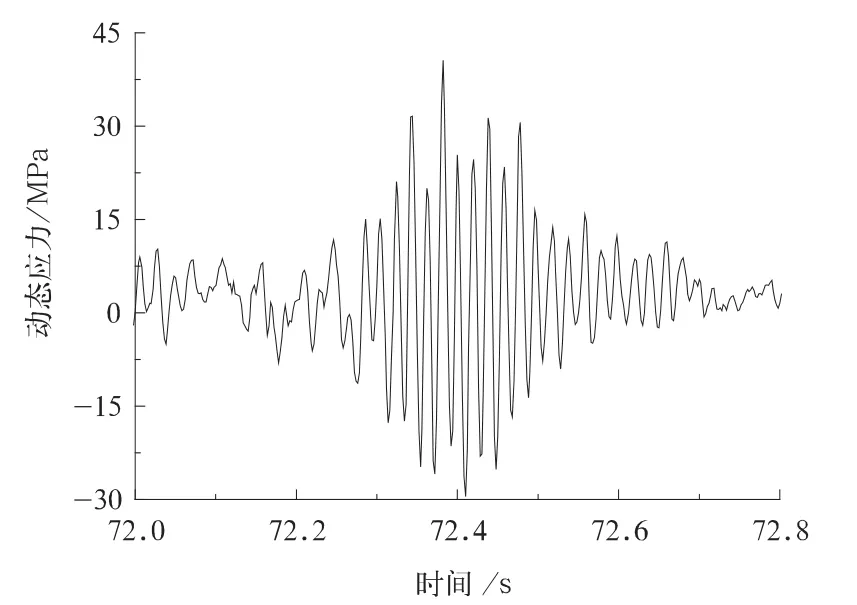
图3 电机吊座周围测点65动应力特点

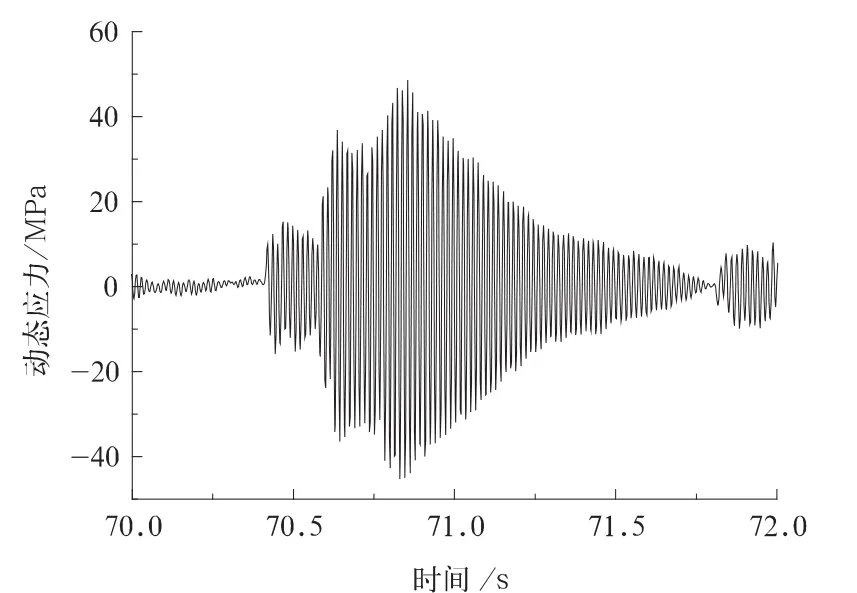
图4 ATP天线梁周围测点动应力特点

对图3所示弹性振动动应力时间历程进行FFT变换，得到测点65的动应力频谱图。图5所示为测点82和测点65的动应力频谱对比图。由此可见，电机吊座周围测点65弹性振动主振频率为50.8 Hz，而测点82相比测点65没有明显的弹性主振频率。

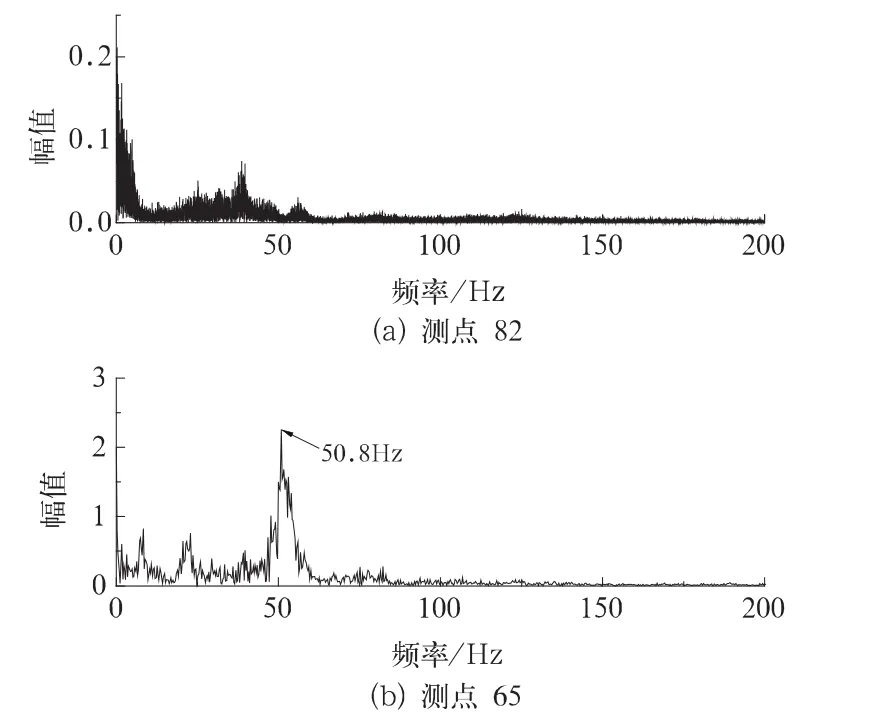
图5 测点82、65动应力频谱图

2 构架模态分析

地铁车辆转向架构架在动应力作用下发生的破坏属于结构振动疲劳破坏。结构疲劳破坏中包含的一类重要问题是如果交变载荷的频率与结构的某一阶和某几阶共振频率一致或相接近时，结构将会发生共振，这时一定的激励将会产生更大的响应，以致更加易于产生破坏［8］。

因此，为了进一步确认上述频率50.8 Hz是否为构架固有振动频率，这里对构架进行模态分析，得到其前6阶弹性振动模态。

2.1 构架有限元模型建立

利用大型通用建模软件Solidworks建立地铁车辆构架实体模型，通过标准数据接口将构架实体模型以IGES格式导入HyperMesh软件中采用四面体单元进行网格划分，参照构架的几何尺寸确定网格尺寸，得到构架的有限元模型。

2.2 构架模态分析

利用Ansys中的模态计算功能，对构架的模态频率进行提取，分析中采用了Block Lanczos法［9］。考虑电机悬挂质量后，构架在一定频率范围内的振动模态如表1所示。由此可见，频率50.8 Hz与两横梁水平面一阶弯曲51.1 Hz(相差近0.587%)比较接近，存在局部范围的共振。

表1 各阶振动模态

3 弹性振动对疲劳寿命影响

3.1 疲劳寿命计算方法

实际运用中，转向架构架动应力是一个随时间变化的复杂历程，在疲劳寿命研究时首先采用雨流计数法，将动应力的整个时间历程整理成由若干级大小不同、循环次数不等的应力水平所构成的应力谱。转向架结构通常取8级应力谱，即能可靠地反映实际的动应力历程。

Miner理论认为材料的疲劳破坏是由于循环载荷不断作用产生的损伤不断积累造成，疲劳损伤达到破坏时吸收的净功与疲劳载荷的加载历史无关，并且材料的疲劳损伤程度与应力循环次数成正比［10］。大量实验证明，Miner线性累积损伤为1时，认为被评估对象开始产生疲劳破坏。采用 Miner线性累计损伤法则［11］和NASA［11］针对变幅加载条件所推荐的S－N曲线形式计算等效应力幅，可使各级应力水平产生的损伤均得到合理的考虑。

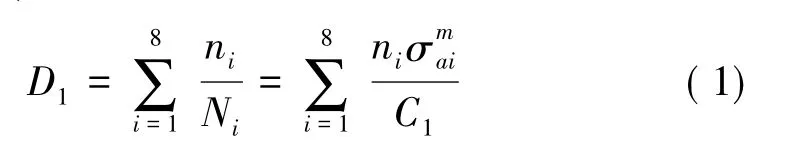
由Miner线性疲劳累计损伤法则，应力谱产生的损伤D1可由式(1)确定。式(1)中，ni是与各级应力水平对应的应力循环次数，即各测点应力谱中各级应力的出现次数;C1为S－N曲线参数，m为材料系数，对于普通钢焊接结构一般取3.5，对于普通母材一般取5～7;σai为各级应力水平的幅值，Ni是各级应力下循环到破坏的总循环次数。对于任何部件，在使用寿命期限内，其累积损伤是一定值［12］。

设等效应力幅σaeq作用N次后，结构产生的损伤为D，(N是与结构或材料的疲劳极限所对应的循环次数，对于焊接结构一般取200万次，对于母材一般取1 000万次)，即

假设实测应力谱运行公里数为L1(本次试验公里数为192 km)，一个应力谱产生的损伤为D1，产生总损伤D的安全运行里程为L km，那么由式(3)成立［13］。

代入D和D1的表达式，可得:

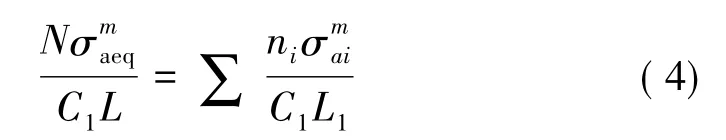
由此，等效应力幅计算公式如式(5)所示。

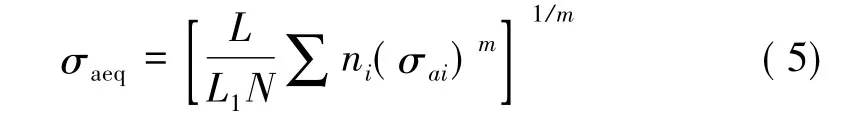
3.2 电机吊座典型测点应力谱

采用雨流计数法，将测试得到的各测点动应力时间历程进行分析与统计，并编制了构架动应力幅值较大测点的应力谱。由于篇幅有限，表2列出了转向架构架电机吊座上应力幅值较大、弹性振动明显的3个测点的动应力幅值谱。由此可见，其最大应力均接近或者超过50 MPa。

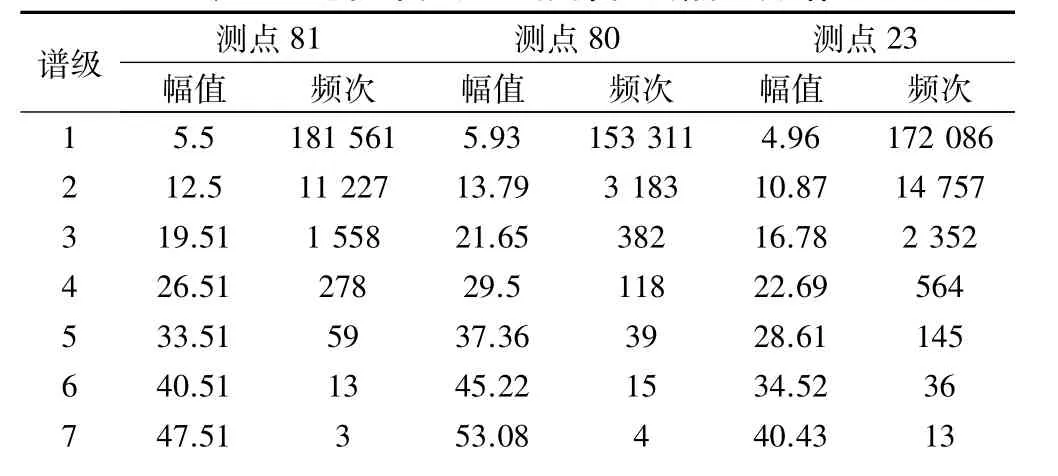
表2 电机吊座加强板部位测点应力谱

3.3 疲劳寿命影响分析

由式(1)可知，应力幅值增大和频次增加，均会引起构架损伤增大。事实上，发生弹性振动后，构架局部动应力幅值增大的同时，其作用频次显著增加。弹性振动对疲劳寿命的影响，目前还没有相关理论和方法对其进行统计和研究。对发生弹性振动的应力测点，这里采用去除弹性振动主频率的方法，对其动应力测试数据进行处理，并对比去除主振频率前后测点等效应力变化，研究弹性振动对疲劳寿命的影响。

对构架上发生弹性振动的测点，采用带阻滤波方式，滤除与弹性振动频率有关的应力幅值和作用频次。由前面可知，这里的弹性振动主频率为50.8 Hz，因此对其进行49～52 Hz带阻滤波处理，滤波后的结果可认为是未发生弹性振动的动应力值。

图6对比了应力测点65滤波前后的动应力变化。与滤波前相比，滤波后与上述带阻频率对应的动应力幅值有所减小，其他频率范围内动应力幅值和频次，均未发生任何改变。

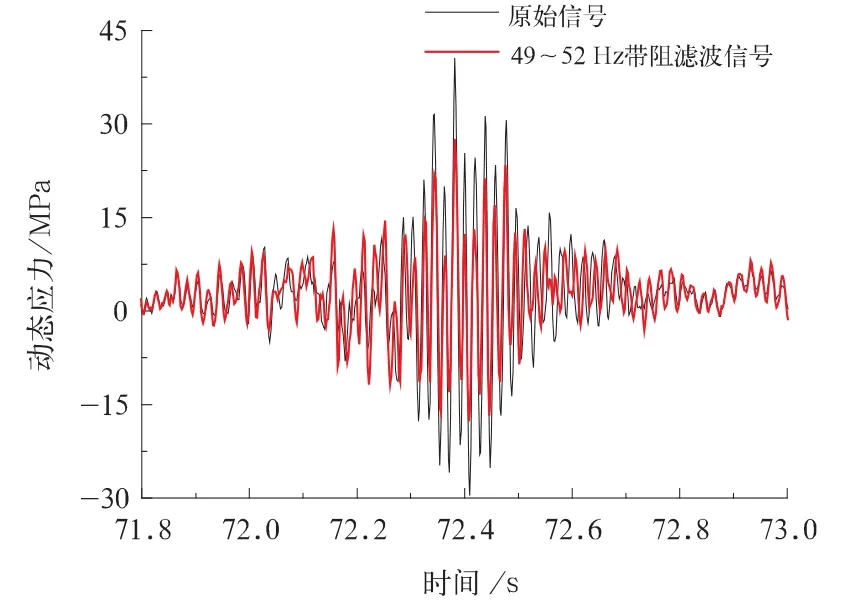
图6 去除主频率处理前后动应力对比(测点65)

依据上述方法和式(5)，得到的电机吊座周围3测点滤波前后最大应力(σmax)、最小应力(σmin)以及等效应力幅值(σaeq)如表3所示。

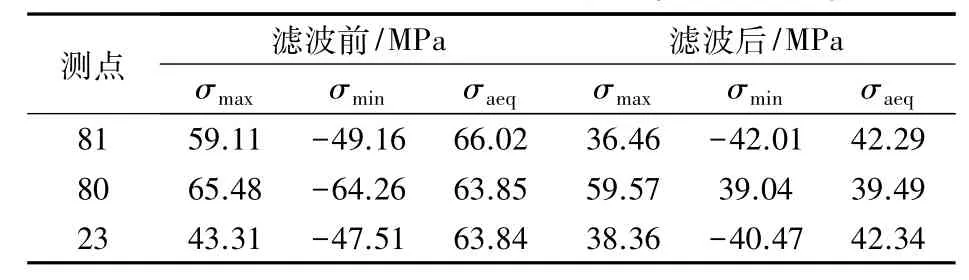
表3 典型测点去除主频率处理前后等效应力幅值对比

由表3可知，去除主频率后测点的σmax，σmin，σaeq均有一定程度的减小。事实上，采用该种方法处理后，弹性振动引起的测点动应力放大部分被去除，刚性振动引起的动应力值得到保留。

图7给出了构架上主要应力测点带阻滤波前后360万运行里程时对应的等效应力幅值，图中为了将构架上相同部位测点的数据处理结果绘制在一起，对测点进行了重新编号，因此图7中横坐标的测点编号并非线路动应力测试时的测点号。由此可见，去除主频率处理后，几乎所有测点的等效应力幅值都有一定程度的减小，且减小程度越大表明弹性振动越明显;电机吊座周围的大多数测点相对其他部位测点的等效应力幅值在振动前后相差较大，表明电机吊座周围测点弹性振动较其他部位明显;此外，齿轮箱吊座、小纵梁与横梁连接处部分测点的等效应力值在振动前后也有一定的差异，表明这些部位也发生了一定程度的弹性振动。

图7 滤波前后测点等效应力幅值比较

由式(1)和式(2)可知，结构损伤与其等效应力之间有材料指数m之间关系。因此，等效应力越大，其使用寿命越低，且呈指数m减小。图8给出了主要测点360万运用里程下，构架主要测点滤波后等效应力和滤波前等效应力比值，以及由此引起的使用寿命比值差异。测点82和测点65的使用寿命偏差值已在图8中标出。

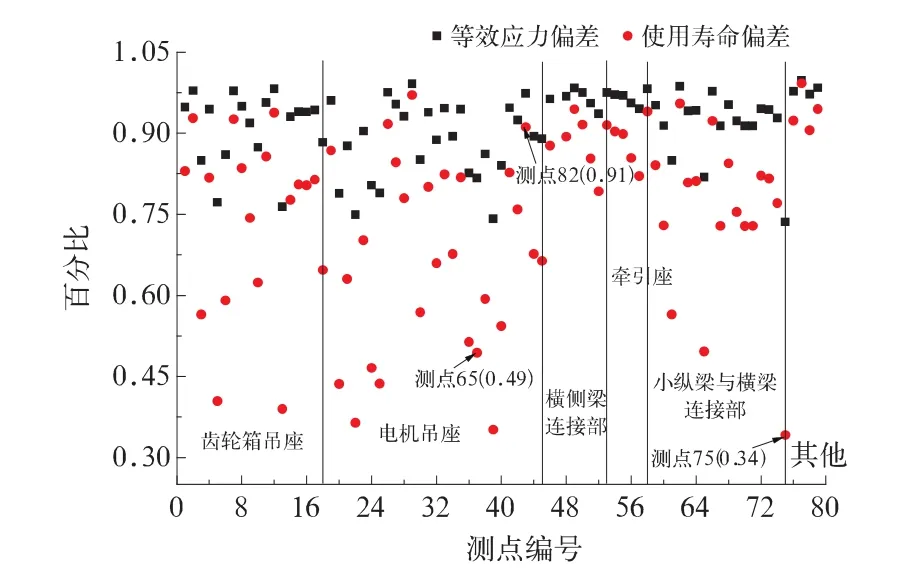
图8 构架上测点等效应力与使用寿命偏差比较(测点编号含义同图7)

由此可见，与未发生弹性振动相比，发生弹性振动后测点的使用寿命会有所降低，最大使用寿命偏差值为34%(测点75)，即发生弹性振动后，其使用寿命变为原设计寿命的1/3。另外，如果测点未发生弹性振动，则该测点等效寿命完全一致，在图8中表现为等效应力比值和使用寿命比值均为1的测点，这也验证了研究方法的可信性。

4 结论

通过线路测试并在获得构架振动模态基础上，对发生弹性振动测点的动应力进行主振频率滤波，获得了车辆转向架构架典型测点动应力谱及弹性振动对构架使用寿命影响特性。研究结果表明:

(1)与未发生弹性振动测点的动应力相比，发生弹性振动测点的动应力幅值明显增大、作用频次明显增加;

(2)采用滤波方法去除弹性振动影响后，等效应力和使用寿命偏差表明，发生弹性振动后疲劳寿命降低，约为原设计寿命的1/3或者更低。

利用实测数据和有限元方法，对构架局部位置弹性振动进行了确认，对弹性振动引起的结构寿命影响进行了研究。需要说明，探索引起构架弹性振动因素以及如何避免这一问题，应是下一步重点研究的内容之一。

［1］ 刘晓雪，杨睿璋，佟维.基于动应力计算的构架疲劳寿命分析［J］.内燃机车，2012，(6):27-30.

［2］ 贾倩，程祖国.基于动应力试验的转向架构架疲劳寿命预测［J］.铁道机车车辆，2010，30(4):65-68.

［3］ 任尊松，孙守光，李强，等.构架结构振动与动态应力仿真研究［J］.机械工程学报，2004，40(8):187-192.

［4］ 王成国，孟广伟，原亮明，等.新型高速客车构架疲劳寿命数值仿真分析［J］.铁道学报.2004，26(4):42-45.

［5］ Claus H，Schiehlen W.Modeling and simulation of railway bogie structural vibrations［J］.Vehicle Systems Dynamics Supplement，1988，28:538-552.

［6］ Stefan Dietz，Helmuth Netter，Delf Sachau.Fatigue Life Prediction of a Railway Bogie under Dynamic Loads through Simulation［J］.Vehicle Systems Dynamics Supplement 1998，29: 385-402.

［7］ 金新灿.通过道岔时转向架结构振动与动应力分析［D］.北京交通大学博士论文，2006.

［8］ 姚起杭，姚军.工程结构的振动疲劳问题［J］.应用力学学报，2006，23(1):12-15.

［9］ 袁安富，陈俊.ANSYS在模态分析中的应用［J］.中国制造业信息化，2007，36(11):42-44.

［10］ 杨爽.CRH3型高速动车组转向架抗疲劳能力研究［D］.大连:大连交通大学硕士学位论文，2009.

［11］ 赵少汴.抗疲劳设计［M］.北京:机械工业出版社，1997.

［12］ 濮良贵，纪名刚.机械设计［M］.北京:高等教育出版社，2006.

［13］ 姚卫星.结构疲劳寿命分析［M］.北京:国防工业出版社，2003.

Research on the Influence of Railway Bogie Elastic Vibration to Fatigue Life

ZHANG Li，REN Zunsong，SUN Shouguang，YANG Guang
(College of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University.Beijing 100044，China)

In recent years，the elastic vibration problems has occurred repeatedly in the bogie frame of domestic metro vehicle and its influence on the fatigue life of bogie has been paid high attention.Based on the analysis of dynamic stress test results of the key position points on some type of domestic metro vehicle bogie in time domain and frequency domain，this study achieves the dynamic stress distribution characteristics of the vibration test points on bogie frame.And then the FEM model of the bogie is established to calculate its free vibration frequency.Results show that the elastic vibration frequency of the bogie in service is consistent with a natural frequency.Adopting the method of removing the domain vibration frequency to process the test data，this study obtains the dynamic stress distribution characteristics in time domain of removing the vibration frequency.According to the Rain-flow Counting Method、S－N Curve and Miner Linear Damage Cumulative Rules，the equivalent stress amplitude and fatigue life of test points on different parts of the bogie on elastic vibration and removing elastic vibration circumstances are achieved，so that，the structural elastic vibration characteristics of fatigue life can be obtained.The results show that the fatigue life of the test points on local positions of the bogie frame will drop substantially after the elastic vibration occurs and the minimum can be reduced to the original design life of 1/3.

bogie;dynamic stress;elastic vibration;fatigue life;influence

U239.5

A

10.3969/j.issn.1008－7842.2015.02.28

1008－7842(2015)02－0115－05

*国家自然科学基金(51175032、U1134201);铁道部重大科研计划项目(2012J009－A)张丽(1988—)女，硕士研究生(

2014－09－05)