基于加速度信号的纵跳力学参数计算

贾菲菲，宾光宇，吴水才，师玉涛

1. 北京工业大学，北京 100124；2. 北京市体育科学研究所，北京 100075

基于加速度信号的纵跳力学参数计算

贾菲菲1，宾光宇1，吴水才1，师玉涛2

1. 北京工业大学，北京 100124；2. 北京市体育科学研究所，北京 100075

目的 使用加速度传感器信号计算纵跳的离地速度、纵跳高度，并对纵跳高度与爆发力进行回归分析。方法 嘱受试者佩戴爆发力测试仪和含有加速度传感器模块的仪器纵跳10次，记录其纵跳过程中的离地速度、纵跳高度、爆发力以及加速度信号，使用加速度信号积分计算离地速度、腾空时间，使用时域积分计算纵跳高度及纵跳高度非线性拟合爆发力。结果 使用积分法计算离地速度的误差为5.9％，使用腾空法和积分法计算纵跳高度的误差为14.0％和8.2％。对纵跳高度与爆发力进行回归分析，误差为6.2％。结论 使用加速度传感器信号计算和拟合人体运动参数，结果误差较小，可以用于人体运动的检测，也可以为日常人体锻炼监测设备的设计提供参考。

加速度传感器；纵跳高度；离地速度；非线性拟合爆发力；加速度信号积分；时域积分

纵跳在体育运动中的作用不言而喻，纵跳能力的高低有时候甚至能成为某项运动成绩好坏的决定因素[1]。纵跳主要可以分成蹲跳、下蹲跳和连续纵跳等。纵跳参数的测量一般使用测力台或者爆发力测试仪，但是测力台体积大，对使用场地有一定的要求；市场上的爆发力测试仪则价格昂贵，难以普及。

随着传感器技术的发展，加速度传感器的精度不断提高、体积逐渐减小。在生物医学工程应用方面，加速度传感器可以用于测量人体加速度信号。由经典力学知识可知，使用加速度信号积分可以计算速度，进而计算力学的其他参数。本研究使用三轴加速度传感器（型号为ADXL345）获取人体纵跳时的加速度信号，再使用预处理后的加速度信号计算纵跳的离地速度、纵跳高度等力学参数，将所得数值与现有的爆发力测试仪的数据对比，探讨基于加速度信号的纵跳力学参数计算方法的可行性。

1 材料与方法

（1）受试者：身高为（185±5）cm、体重为（71±3.5）kg、无下肢病史的3名健康男性。实验过程中，实验者腰间佩戴爆发力测试仪以及含加速度传感器模块的仪器，两种仪器在腰间的距离左右对称。

（2）实验过程：①双手叉腰（避免手臂摆动影响运动效果）；②站直等待1~2 s；③自由预蹲至膝屈90°，并尽最大努力向上跳起；④采用正常动作下落，并站直1~2 s；⑤重复上述步骤，共纵跳10次。

（3）实验数据采集：人体加速度信号使用三轴加速度传感器采集，采集到的数据通过蓝牙接收，并显示、储存在计算机中。加速度传感器的数据采样频率为1000 Hz。爆发力测试仪使用Perforembetter品牌，该测试仪可以记录纵跳的离地速度、纵跳高度以及爆发力。参数计算时，使用爆发力测试仪所测数据作为标准值。

2 结果

本研究使用matlab软件对人体纵跳时获取的加速度信号进行预处理、计算、回归分析。由于获得的原始信号还包含了仪器以及身体抖动所产生的噪声，故在进行数值计算之前需要去除噪声，本研究使用50点光滑滤波来滤除噪声。纵跳过程中，垂直方向的加速度加大，另外两个方向的加速度值很小，本研究使用加速度传感器垂直方向矫正算法找到垂直方向的加速度来计算离地速度等参数[2]。预处理后的信号波形，见图1。

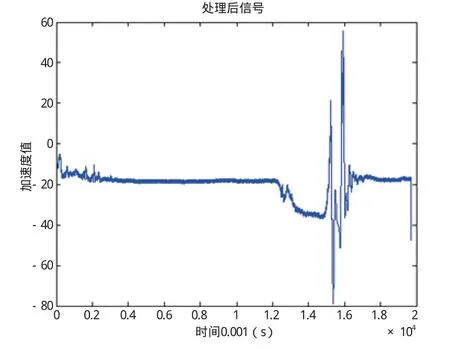
纵跳过程：纵跳是由人体肌肉发力，产生对地面的向下作用力，通过地面的反作用力提供人体向上的速度，涉及力、加速度的变化及能量的转化[3-4]。由图1可以看出，人体静止时，加速度几乎不变；接着下蹲助跳时，加速度方向向下；而后在极短时间内，人体重心运动方向由向下变为向上，人体获得向上的速度，之后有一段腾空时间，这段时间内人的速度由向上变成向下，人体只受到重力的作用，加速度向下；最后，人体落地，地面给人体一个缓冲力，人体加速度向上，有一个向上的峰值，之后人体静止，加速度不变。

2.1 纵跳离地速度

依据上述分析，在跳起的瞬间人体可以获得最大的瞬时加速度，则此刻人的速度为：

其中使用垂直方向加速度，t是加速度最大值时刻，t1是0时刻。常用的处理积分的方法有时域法和频域法两种[5-6]。频域法有低频截止频率敏感性，低频截止频率选择不当会造成积分结果有很大误差。由图1可以看出，t时刻之前的加速度信号比较平稳，适合使用时域积分。由于直流分量的存在，在进行时域积分时需要消除趋势以得到更为精确的结果[7]。数字积分的方法很多，其中梯形公式因其计算方法简单、计算精度较高而被广泛采用。本研究即使用该方法进行积分，计算结果的平均误差为5.9％。经积分计算的离地速度与爆发力测试仪所测的离地速度对比结果，见图2。其中1名受试者经爆发力测试仪所测数据，见表1。

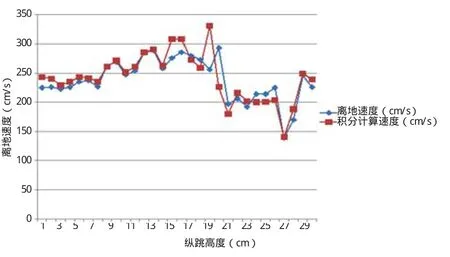
图2 经积分计算的离地速度与爆发力测试仪所测的离地速度对比结果

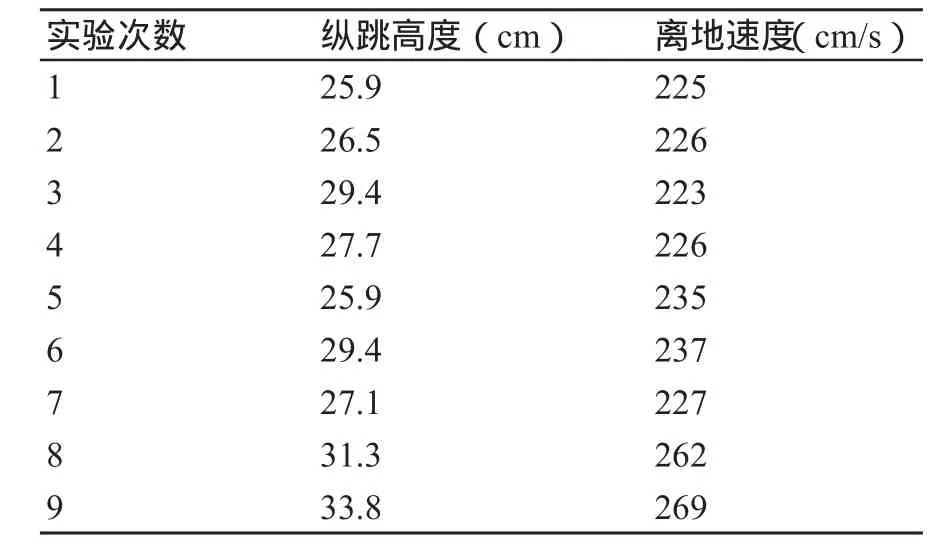
表1 1名受试者经爆发力测试仪所测数据

2.2 纵跳高度

2.2.1 腾空时间法

纵跳高度在弹跳能力的体质评价与临床诊断等方面已有广泛应用。纵跳高度的测试方法有几种，有文献[8]提出使用动能定理计算纵跳高度，即根据经典力学公式分析，人体离地速度应该和落地速度相等，这样就能很方便地使用动能定理推算纵跳高度。但从表1中第一次和第三次的纵跳数据可知，较大的离地速度并没有产生较高的纵跳速度，因此纵跳过程并不完全符合动能原理。

文献[9]通过使用测力平台计算起跳的冲量，进而计算纵跳高度。文献[10]则使用腾空时间法来计算纵跳高度。采用腾空时间法计算纵跳高度是一种较为普遍的方法，本研究首先使用腾空时间法来计算纵跳高度。腾空时间是离地时间和落地时间的差值，假设一个运动物体的初速度为，加速度为 ，则在运动时间t内所经过的距离h为：

计算出起跳时的离地速度和空中的运动时间t，就可以利用公式估算出纵跳高度。

纵跳过程包括起跳、腾空和落地，采集到的加速度信号并不是只有起跳到落地这段时间的信号，还包括起跳前和落地后人体运动的加速度信号，通过观察加速度信号波形，发现所有的波形都会在一段时间内数值几乎保持不变，也就是出现腾空现象[11-13]。

设加速度信号第一个突然变向并且增大的时刻为离地时刻，离地时刻后加速度值在一段时间内保持不变；再设下一个加速度值突然变向的时刻为落地时刻，则腾空时间的计算如下公式：

通过腾空现象可以很好地估计出纵跳时间，纵跳高度的时间则是这个时间的1/2，记为0.5*t，使用上文计算的离地速度可以计算出受试者的纵跳高度。离地速度向上和重力加速度方向，a取-9.8。经腾空时间法计算的纵跳高度与爆发力测试仪所测的纵跳高度对比结果，见图3。

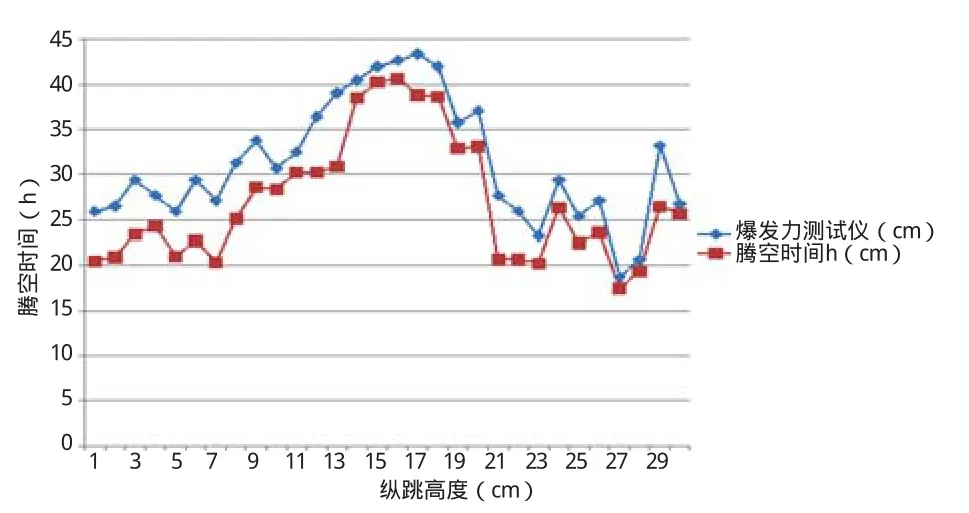
图3 经腾空时间法计算的纵跳高度和爆发力测试仪所测的纵跳高度对比结果

文献[10]研究表明，使用腾空时间法计算出的纵跳高度要明显小于实际纵跳高度，误差在20％左右，和本研究误差14.0％较为近似。因此，使用腾空时间法计算纵跳高度需要改进，而为了进一步提高准确率，考虑使用速度积分计算纵跳高度。

2.2.2 时域积分法

首先，对加速度信号进行频谱分析，可知加速度信号是低频信号，受频截止频率影响较大，故选择时域法计算纵跳高度[14-15]。计算公式如下：

经时域积分计算的纵跳高度与爆发力测试仪所测的纵跳高度对比结果，见图4。由于人体纵跳到最高点过程中的加速度信号较为平缓，而且腾空时间过程中人体加速度信号几乎不变为-g，在积分之前对腾空时间段的加速度信号进行均值滤波，经时域积分计算的纵跳高度的平均误差为8.2％，相对于腾空时间法误差较小。

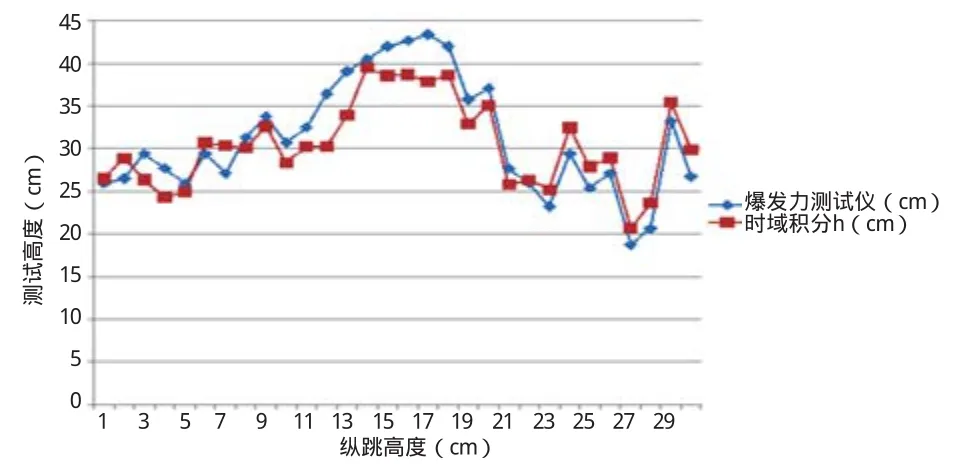
图4 经时域积分计算的纵跳高度与爆发力测试仪所测的纵跳高度对比结果

2.3 爆发力和纵跳高度回归分析

对爆发力定义的界定虽然不尽相同，但爆发力的实质却是相同的，即表示极短时间内的力数值的变化[16-18]。爆发力是由人体肌肉产生的力，难以直接计算。但是爆发力产生的效果可以由离地速度和纵跳高度间接表示。

回归分析是研究相关关系的一种统计方法。首先，通过对爆发力测试仪记录的数据作散点图（图5），发现纵跳高度和爆发力分布趋势难以使用线性拟合，而更适合使用非线性回归法。本研究对使用积分计算出的纵跳高度和爆发力进行回归分析，用误差来表示结果的准确性。实验结果表明：非线性回归法计算的平均误差为6.2％，相比于最小二乘法平均的效果好（误差为6.6％），其回归模型为：

F=32.27h-0.08+sin(7.3h） (5）

式中，F为爆发力，h为纵跳高度。需要说明的是，实验所用的爆发力测试仪所定义的爆发力单位为N/kg，文本计算的单位与之一致。虽然爆发力和纵跳高度有关，但并不是唯一的影响因素，受训练水平、动作协调性等因素同样影响纵跳高度。经拟合计算的爆发力与爆发力测试仪所测的爆发力对比结果，见图6。

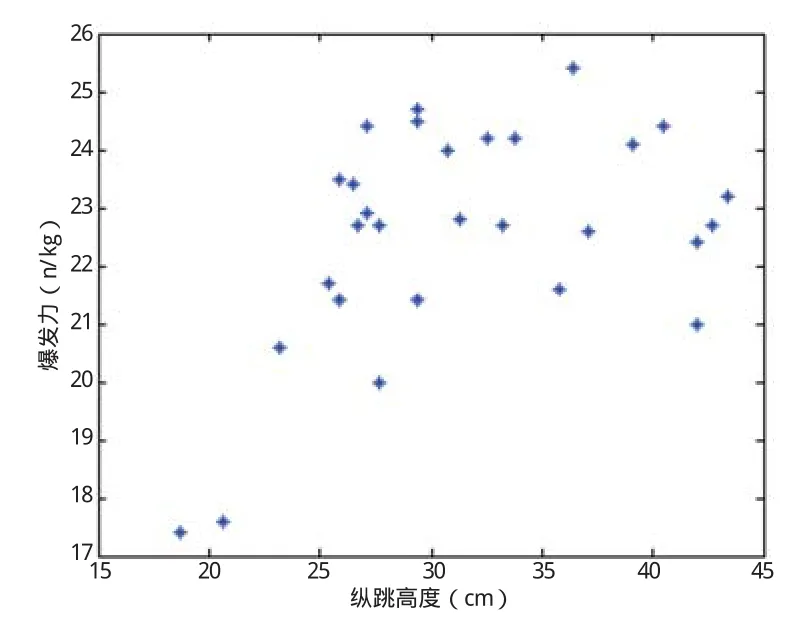
图5 纵跳高度-爆发力散点图

图6 经拟合计算的爆发力与爆发力测试仪所测的爆发力对比结果

3 讨论

不能简单将人体看作单个质点，因为人体纵跳过程中各个关节并不是全部伸直，地面反作用力也没有全部做功，在传输的过程中有一定的损耗。同时，人体也不是刚性物体，除经典力学之外，人体运动需要考虑更多因素[19]。总的来说，人体纵跳是人体各关节、肌肉的共同作用，而各关节角度是由人体的中枢神经系统进行调控，并受人体协调能力的影响。力学参数计算、回归分析时需要考虑更多的人体运动力学理论。

4 结论

本研究使用加速度传感器信号计算和拟合人体运动参数，结果误差较小。该方法可以用于人体运动的检测，可以为日常人体锻炼监测设备的设计提供参考。不过，本研究尚有一定问题需要解决，比如实验中人体左右力学参数不完全对称，数据采集有一定的改进空间；同时人体爆发力需要进一步计算等。

[1]马明.不同负荷对原地连续纵跳生物力学特征影响的研究[D].济南：山东师范大学,2011.

[2]Zhenyu He,Zhibin Liu,Linwen Jin.W eightlessness feature-a novel feature for single tri-axial accelerometer based activity recognition[A].19th International Conference on Pattern Recognition IEEE[C].2008.

[3]霍兴华.单、双腿纵跳爆发力练习的比较研究[J].体育与科学, 2014,(4）：106-109.

[4]于渤洋.摆臂对纵跳影响的生物力学机制研究[D].苏州：苏州大学,2012.

[5]李金艳.时域积分方程时间步进算法及其快速算法研究[D].成都：电子科技大学,2013.

[6]周英杰.加速度测试积分位移算法及其应用研究[D].重庆：重庆大学,2013.

[7]周东明.时域积分方程快速算法及其应用研究[D].长沙：国防科学技术大学,2006.

[8]王坦,傅水根,吴平东.人体纵跳高度的间接测量方法[J].中国农业大学学报,2003,(6）：42-44.

[9]王建军,张元良.纵跳高度测量系统研究[J].中国仪器仪表,2009, (12）：61-64.

[10]单信海,丁萌.纵跳高度腾空时间计算法的理论探讨与实验评价[J].中国临床康复,2004,(24）：5103-5105.

[11]赵西堂.我国男子排球一级运动员摆臂和并步移动对纵跳的影响[D].北京：北京体育大学,2009.

[12]杨多多,苏美华.足不同背屈纵跳高度的生物力学分析[J].河北体育学院学报,2012,(2）：74-76.

[13]郑亦华,叶永延.下肢某些肌肉活动、膝角和纵跳效果的生物力学分析[J].苏州大学学报(自然科学版）,1986,(2）：189-193.

[14]张英媛.下肢不对称性及其在单双腿起跳中的生物力学表现[D].苏州：苏州大学,2013.

[15]曹玉珍,刘晓婷,程旸.基于加速度的人体步态监测方法[J].中国医疗设备,2009,24(2）：60-62.

[16]武丽平.不同负重杠铃下蹲对纵跳成绩的短时影响[D].西安：西安体育学院,2014.

[17]曹志飞.原地连续纵跳的运动生物力学研究[D].烟台：鲁东大学,2010.

[18]张佑磊.下肢肌肉力量与不同形式纵跳运动学和动力学特性相关度的研究[D].苏州：苏州大学,2012.

[19]李泽亚.劣势腿力量改善对助跑双脚纵跳高度影响的实证研究[D].北京：北京体育大学,2013.

Calculation of Longitudinal Jum p Parameters Based on Acceleration Signals

JIA Fei-fei1, BIN Guang-yu1, WU Shui-cai1, SHI Yu-tao2
1.Beijing University of Technology, Beijing 100124, China；2.Beijing Research Institute of Sports Science, Beijing 100075, China

Objective Using the acceleration sensor signals to calculate the off-ground speed and height of the vertical jump and to make regression analysis of its height and the explosive force. Methods The experimenter was required to wear an explosive force tester and an instrument containing an acceleration sensor module andvertically jump 10 times. The off-ground speed, height, explosive force and acceleration signals were recorded during the vertical jump process. Then, the acceleration signal integral was adopted to calculate the off-ground speed and duration of passage；the height of vertical jump and its nonlinear fitting explosive force were calculated by using the time-domain integral. Resu lts The integral method produced a 5.9％ error in calculation of the off-round speed；while, the time-domain integral method produced a 8.2％ error versus the jump method’s 14.0％ in calculation of the height of jumping. Through regression analysis of the height and the explosive force of the vertical jump, the error of the regression model was 6.2％. Conclusion Using the sensor signal of the acceleration sensor to calculate and fi t body animation parameters can be used to detect human motion or provide certain reference for the design of monitoring equipment of daily exercise.

acceleration sensor signals；height of vertical jump；off-round speed；nonlinear fitting explosive force；acceleration signal integral；time-domain integral

TP391.41

A

10.3969/j.issn.1674-1633.2015.09.004

1674-1633(2015）09-0016-04

2015-06-08

2015-06-16基金项目：国家自然科学基金项目资助（61105123）。

作者邮箱：945639850@qq.com