五轴数控加工非线性误差分析及控制策略*

2015-05-31中航工业沈阳飞机工业集团有限公司刘本刚王碧玲

航空制造技术 2015年15期

中航工业沈阳飞机工业(集团)有限公司刘本刚王碧玲

93057部队机务处王石

沈阳高精数控技术有限公司郑缪默

五轴联动数控加工技术是实现复杂自由曲面加工的关键技术，在航空制造领域的应用极为广泛。但是,五轴加工中实际刀轨常偏离加工表面引起非线性误差[1]，如航空薄壁件外轮廓加工时，表面产生周期性的起伏，这是由于旋转轴插补运动在与走刀方向垂直的平面内引起的非线性误差造成的。樊曙天等[2]通过集成RTCP功能使系统实时进行线性补偿，有效地减小了旋转轴插补在走刀平面内引起的非线性误差。杨旭静等[3]提出了通过限制两相邻刀位点之间刀轴矢量夹角的方法来控制与走刀垂直的平面内的非线性误差的大小，但此方法随着控制精度提高，程序段数量剧增，增加了数控系统的处理时间，并且无法消除该非线性误差。樊留群等[4]提出了刀轴矢量平面插补算法，通过仿真验证该方法从根本上解决了旋转轴插补在与走刀垂直的平面内引起的非线性误差，但未提及该插补算法下旋转轴角度和转速变化的连续性及平滑性等问题。文中所讨论的旋转轴插补算法均属于数控系统内部插补运算方法。

本文对常用的两种旋转轴插补方法在与走刀方向垂直的平面内引起的非线性误差进行研究的基础上，通过实例对旋转轴插补过程进行仿真，重点分析刀具姿态误差、旋转轴角度和转速的变化情况，结合航空薄壁件加工试验对旋转轴插补运动产生的非线性误差进行分析，并对矢量插补存在的问题给出了改进策略。

1 非线性加工误差

数控加工用微小线段逼近编程曲线，因此实际加工中刀轨总是有一定的偏差[5]，根据引起的原因不同，分为线性误差与非线性误差。线性误差实质是数控加工用微小直线段来逼近编程曲线产生的偏差，与被加工表面的曲率及程序段长度等有直接关系。

在有转动轴的数控系统通过分段非直线运动逼近加工曲面，照此进行插补运动时所需理想运动包络出来一段波纹起伏的曲面与光滑的编程曲面之间的偏差称为非线性误差[6]。其中，在与走刀方向垂直的平面内的非线性误差是由于旋转轴运动坐标(角度)与刀轴矢量之间的非线性关系使刀轴矢量在插补时偏离了编程曲面造成的，如图1所示，q为编程刀轴矢量，q'为插补刀轴矢量，θ为两者之间的偏差角。与线性误差的根本区别是非线性误差产生在插补程序段内，而不是在整条刀轨上。

2 旋转轴插补运动引起的非线性误差分析

本文以A、C双转台五轴数控机床为例对旋转轴插补运动进行分析。

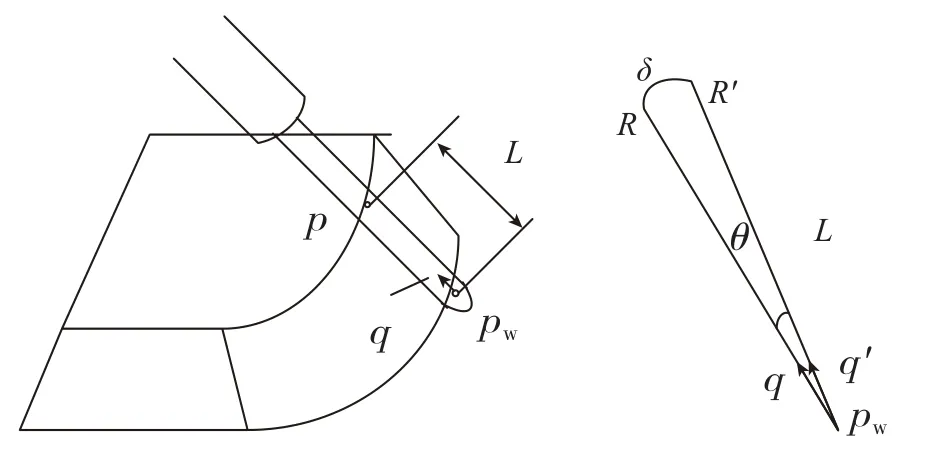
图1 非线性误差示意图Fig.1 Nonlinear error diagram

2.1 A、C五轴机床运动学模型

五坐标加工时，CAM编程软件生成的刀位数据包括刀位矢量p和刀轴矢量q。其中，刀位矢量表示刀具刀尖点的位置，刀轴矢量表示当前刀具的空间姿态。

机床坐标系之间的变换关系，如图2所示，设坐标系Om_XYZ为机床坐标系，与A轴固连，原点为两回转轴的交点；Ow_XYZ为工件坐标系与工件固联；与刀具固联的Ot_XtYtZt称为刀具坐标系，原点在刀尖点上。在工件坐标系下，两回转轴交点Om的位置矢量记为rm(mx,my,mz)，假设编程刀轨上任意点P(p,q)，刀位矢量为rp=pw(px,py,pz)，刀轴矢量为q(i,j,k)。机床旋转轴为A轴和C轴，对应的运动坐标分别为a和c。记机床平动轴相对于初始状态(C轴轴线与主轴平行)的位置为rs(sx,sy,sz) 。

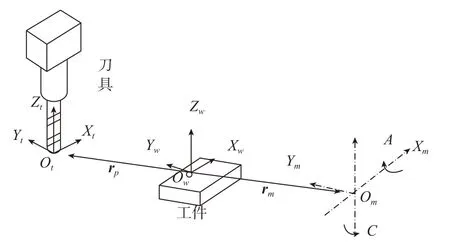
图2 A、C双转台机床坐标系之间的变换关系Fig.2 Transformation relationship between A , C two rotary table machine coordinate system

根据机床坐标系之间的变换关系，该机床的运动学模型[7]：

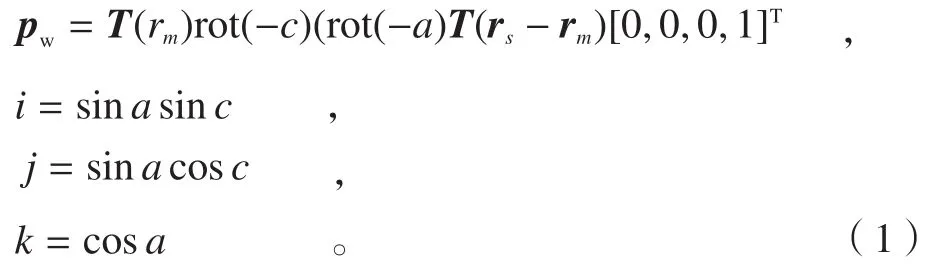
经逆变换，该机床进给轴的运动坐标为：

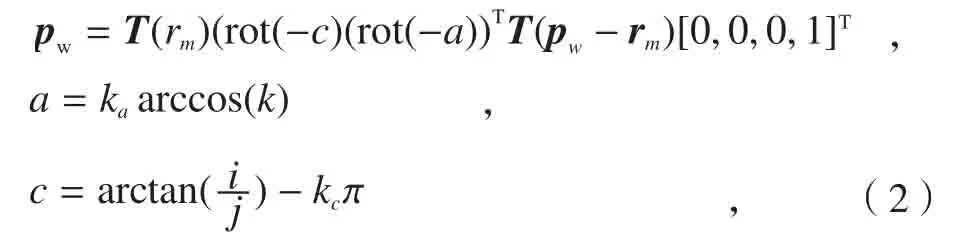
式中，T，R分别为平移和回转运动的齐次坐标变换矩阵；a为A轴旋转角度；c为C轴旋转角度；ka为常系数，ka=-1,1；kc为系数，ka=0,1。

2.2 旋转轴角度线性插补及非线性误差分析

在编程后处理阶段，CAM根据刀位数据按照式(2)计算进给轴的运动坐标，并生成加工程序。数控系统根据加工程序，在相邻刀位点之间进行插补计算，由伺服驱动器根据插补值驱动旋转轴电机控制刀具在刀位点之间运动时的空间姿态。

旋转轴按旋转角度进行线性插值的方式，称为旋转轴角度线性插补[8]，简称线性插补。线性插补策略如下：假设程序段始点S和终点E的刀轴矢量分别为qs(si,sj,sk)和qe(ei,ej,ek)，位置矢量分别为ps(sx,sy,sz)和pe(ex,ey,ez)，运动坐标分别为Ls(sx′,sy′,sz′,as,cs)和Le(ex′,ey′,ez′,ae,ce)。在程序段内分别对A、C轴对应的旋转角度进行n等分，即

式中，i为程序段总线性插补段数。

数控加工时，数控系统将下式计算出的角度值不断发送给旋转轴伺服驱动器，由其控制A、C轴伺服电机准确到达插补值。

式中，i为当前插补点序号。

线性插补通过控制旋转角度的线性变化完成旋转轴的插补运动，因此旋转轴转速变化平滑。但是由于旋转轴角度与刀轴矢量之间的非线性关系，在线性插补运动过程中，刀轴矢量不是线性变化的，即插补过程中的刀轴矢量不在由相邻刀位点的始点刀轴矢量和终点刀轴矢量确定的矢量平面内，该平面是通过将终点刀轴矢量进行平移，保证终点刀轴矢量与始点刀轴矢量的起点重合时两者形成的平面。因此，线性插补时，刀轴矢量会偏离加工表面产生非线性误差。如图3所示是加工型腔内表面时刀轴矢量的变化示意图，由于内表面为斜平面，此时矢量平面即为该斜面，图中虚线为线性插补运动过程中刀轴矢量与零件上表面的交线。

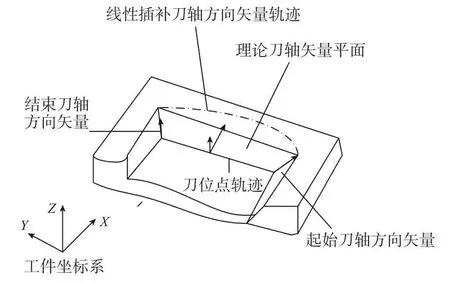
图3 旋转轴角度线性插补示意图Fig.3 Linear interpolation diagram of rotation axis angle

2.3 平面矢量插补及非线性误差分析

平面矢量插补算法是旋转轴在相邻刀位点之间插补时，保证刀轴矢量按线性变化，即始终在程序段始点刀轴矢量和终点刀轴矢量所确定的矢量平面(该平面定义同上)内。矢量插补原理如图4所示，矢量插补由于保证插补过程中刀轴矢量不会偏离编程平面，完全修正了旋转轴角度线性插补产生的非线性误差。但是由公式(2)可知，当刀轴矢量均匀变化时，旋转轴角度按非线性变化，容易产生冲击，且刀轴矢量在奇异点(0,0,1)附近(如j→0，c→∞)的微小变化，可导致旋转轴角度和转速发生急剧变化、产生跨象限等问题，引起机床剧烈震动，导致伺服报警，甚至破坏机床运动机构。矢量插补控制策略如图5所示。

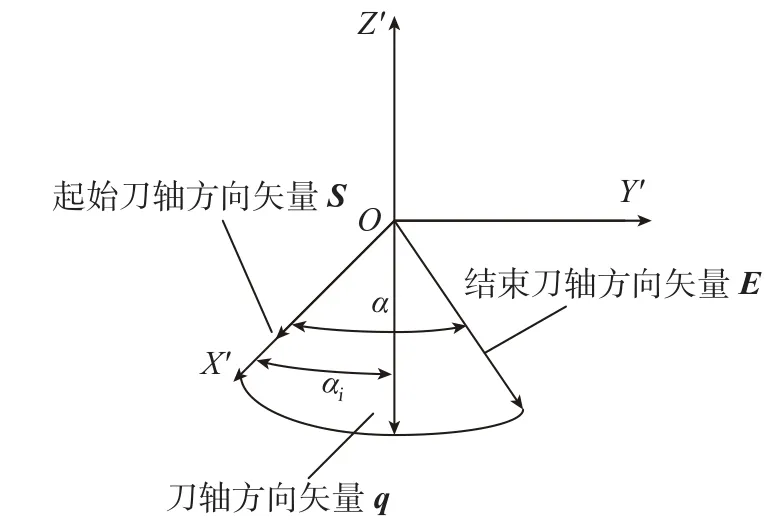
图4 刀轴矢量平面插原理示意图Fig.4 Interpolation principle diagram of cutter axis vector plane

图5 旋转轴矢量插补控制策略Fig.5 Interpolation control strategy of rotation axis vector

以表1中的加工程序段为例，使用MATLAB分别对线性插补和矢量插补过程进行仿真，重点分析旋转轴插补运动过程中刀具姿态误差、旋转轴角位移和角速度的变化情况，仿真结果对比如图6～11所示。

仿真结果(见图6)表明使用线性插补时，刀轴矢量除在程序段始点和终点位置与编程刀轴矢量相同外，整个插补运动过程(程序段内)中刀轴矢量偏离加工表面，且偏移角度最大值发生在程序段中间附近(见图7)。因此，在实际加工时会发生过切或欠切，并且在中间位置过切或欠切量最大，在整条刀轨上表现为周期性的起伏。由于在程序段内旋转轴角度按照相同比例变化，所以旋转轴角度及旋转速度能够实现连续、平滑的变化(见图8～11)。

表1 加工程序段

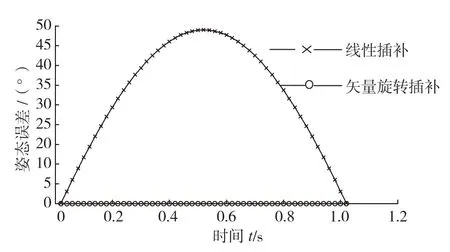
图6 刀具姿态误差分布图Fig.6 Tool posture error distribution

图7 空间刀具姿态示意图Fig.7 Space tool posture diagram

由图6、7可知，矢量插补很好地修正了线性插补引起的非线性加工误差，能够有效解决五轴加工曲面过程产生圆弧型过切或欠切现象，但是旋转轴角位移(见图8、9)和转速(见图 10、11)的仿真结果表明，矢量插补时旋转轴角位移变化显著，转速波动明显，为严重非线性变化，影响零件表面加工质量，尤其是在奇异点附近转速急剧变化甚至突变，易引起机床剧烈振动，导致伺服驱动或系统报警，甚至破坏机床运动机构。

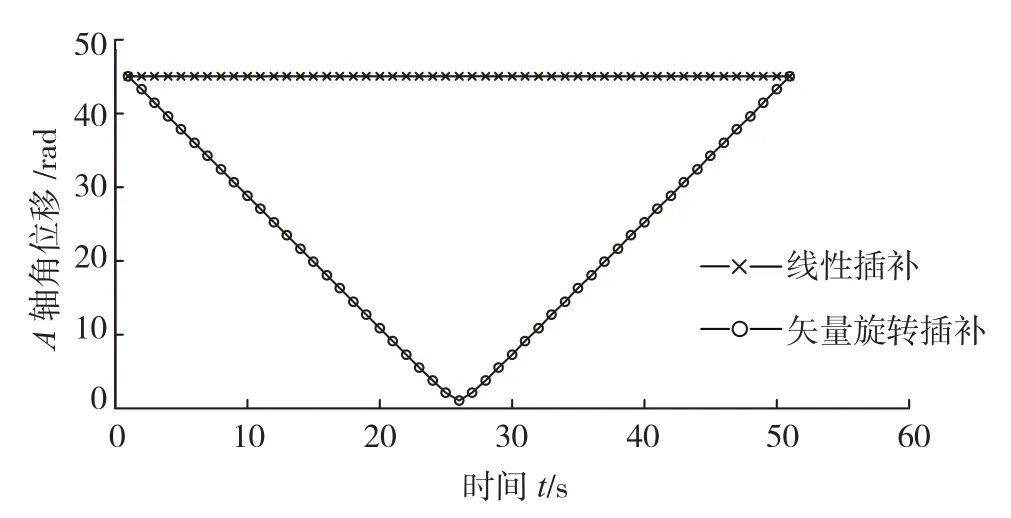
图8 A轴角位移曲线Fig.8 A shaft angular displacement curve

图9 C轴角位移曲线Fig.9 C shaft angular displacement curve

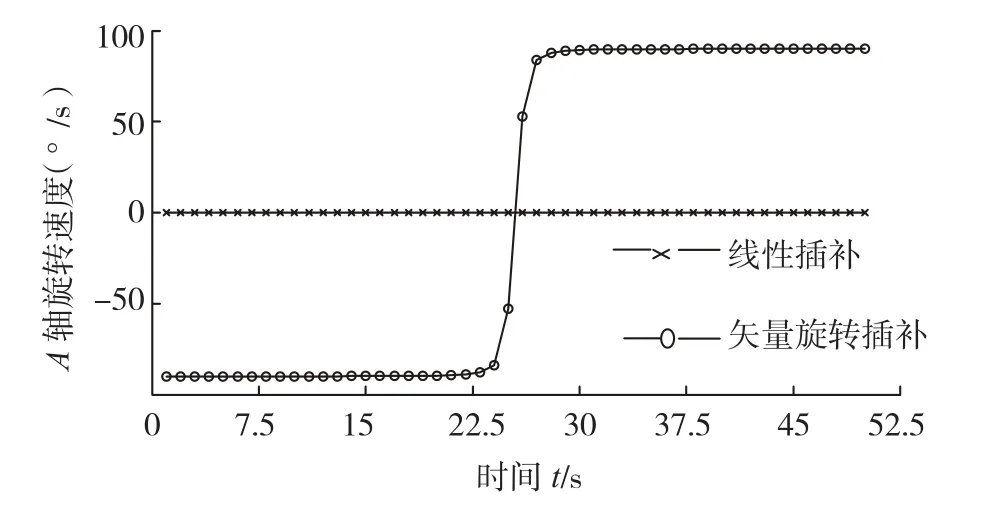
图10 A轴角速度曲线

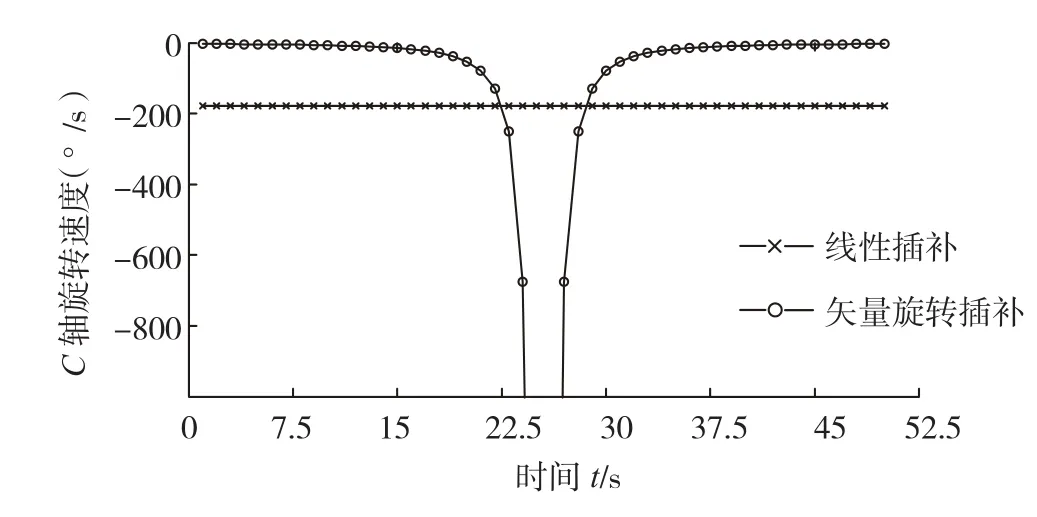
图11 C轴角速度曲线Fig.11 C shaft angular velocity curve

针对矢量插补的特点，使用矢量插补加工航空结构件时，工艺员在编程中应注意以下问题：(1)数控加工进给速度不能太大，否则引起刀轴矢量变化大，导致旋转轴角度和转速急剧变化，使机床承受较大的冲击，影响结构件表面加工质量。(2)避免跨象限问题。总之，矢量插补很好地修正了非线性加工误差，可通过控制切削参数在一定程度上防止旋转轴转速的急剧变化，解决了航空复杂结构件精加工的难题，但是加工效率低，在奇异点附近旋转轴转速发生突变，无法保证运动的平滑性。因此，数控系统需进一步完善旋转轴插补策略，克服矢量插补的局限性。如数控系统通过预读数控程序，使用“智能检测模块”计算并发现加工程序段中存在的奇异点，并在奇异点附近采用线性插补避免旋转轴转速剧烈变化，而其他区域则采用矢量插补避免非线性加工误差，实现精加工要求。