焊接式整体叶盘加工余量自适应优化方法*

西北工业大学现代设计与集成制造技术教育部重点实验室 张 莹 张定华 吴宝海

整体叶盘是新一代高推比航空发动机设计中采用的最新结构和气动布局形式。它将叶片和轮盘直接连接为一整体，大大简化了发动机的结构，进一步提高了发动机的推重比和可靠性。因此，整体叶盘在先进航空发动机中获得了广泛应用[1]。

目前，整体叶盘的制造主要采用复合制造工艺方式，包括精锻制坯＋精密数控加工，焊接制坯＋精密数控加工以及高温合金整体精铸毛坯＋热等静压处理[1-3]。其中，线性摩擦焊接工艺由于具有节省大量贵重金属材料、减少加工时间、综合性能高等优点，成为了整体叶盘制造、维修的理想解决方案，现已成功应用于罗罗、普惠等国外先进航空发动机制造厂商的整体叶盘加工中[2-3]。然而，线性摩擦焊接工艺的误差将使得整体叶盘中不同叶片的相对位置及变形程度存在差异，焊接结果的一致性差，从而导致数控加工过程的装夹定位困难和余量分布不均匀，影响整个叶盘的加工精度[4]。

为此，本文首先分析了整体叶盘的结构特点和制造工艺，然后结合线性摩擦焊接工艺提出了适用于整体叶盘的加工余量自适应优化方法，最后以一算例的详细分析与讨论说明了所提方法的实用性和可靠性。

1 整体叶盘制造工艺分析

航空发动机整体叶盘结构复杂，型面一般为自由曲面且通道开敞性差，加工精度要求高，材料的可加工性差，其综合制造技术属世界级的技术难题，西方发达国家对其严密封锁[3]。

目前，利用多轴数控加工中心实现整体叶盘加工是航空发动机风扇、压气机整体叶盘研制的主要方法之一，其关键技术包括通道可加工性分析、刀轴矢量控制及刀位轨迹规划等几何学优化问题，以及加工过程中的切削参数优化、颤振抑制、弱刚性系统变形控制等力学、物理问题[1]。这种加工方法的显著优点是加工设备简单、精度高；缺点在于加工过程中需要切除大量金属，导致效率低、周期长、成本高，因此也不适于大型及超大型风扇整体叶盘的加工，同时也无法满足批量化生产的要求[2]。

线性摩擦焊接工艺的出现和应用为整体叶盘的近净成形制坯和批量化生产提供了理想的解决方案。但限于焊接工艺的特点和目前的精度水平，焊接完成的整体叶盘仍然需要多轴联动数控加工的方式实现其精加工。就其实现过程而言，无论是整体叶盘的加工还是修复，线性摩擦焊技术的功能相当于完成零件的粗加工，而更严格的加工精度、形状、位置要求需要最终的多轴数控加工手段保证。然而，受焊接变形的影响，叶片的焊接结果一致性差，若直接进行加工，可能导致定位困难或余量分布不均匀，甚至影响整个叶盘的加工精度。此外，在焊接工艺变形的基础上进行加工，过渡区域的设计模型可能不再适应于当前叶片形状的变化，无法实现精密的数控加工[2，5-6]。因此，研究如何实现线性摩擦焊接式整体叶盘高效、精密、自适应的数控加工具有重要意义。

2 加工余量优化建模与求解

受线性摩擦焊接工艺的影响，整体叶盘毛坯中各个叶片的焊接变形程度均可能存在差异，具体体现在各个叶片在叶盘轴向、径向、周向这3个方位所产生的不同程度的焊接误差，从而导致叶盘的定位基准及几何形状均可能需要随之变化，如图1所示。

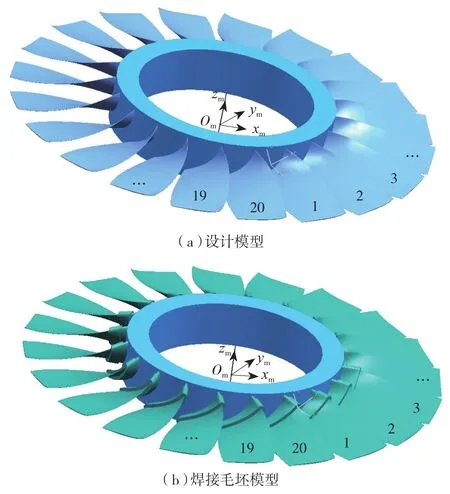
图1 整体叶盘余量优化仿真模型Fig.1 Simulation model for allowance balancing of blisk

因此，本文首先介绍一种通用的加工余量优化建模与求解算法，以便应用于后续的整体叶盘加工余量优化[4]。

设Om-xmymzm为测量坐标系，Ow-xwywzw为工件坐标系，则定位变换定义为测量坐标系到工件坐标系的旋转变换和平移变换（R，t），其变换参数为x=（α，β，γ，Δx，Δy，Δz）T。其中，α、β、γ分别为绕 xw、yw、zw坐标轴的旋转分量，Δx、Δy、Δz分别为沿xw、yw、zw坐标轴方向的平移分量。

设测量坐标系中的测量点集合为P={pi｜i=1，…，N}，则对应工件坐标系内的测量点集合P'={p'i｜i=1，…，N}，p'i=R(x)·p+t(x)；寻找P'={p'i｜i=1，…，N}的对应设计表面最近点集合Q={qi｜i=1，…，N}以及等距的设计表面点集合Q'={q'i｜i=1，…，N}，其中，q'i=qi+δ·ni，ni为qi点在设计表面上的单位法矢，δ≥0为加工余量。

定义有向距离函数：

di(x)=(p'i-q'i)·ni=((R(x)·pi+t(x))-qi)·ni-δ ，

并建立加工余量自适应优化数学模型：

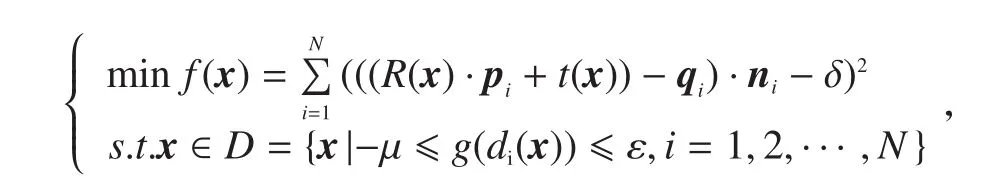
其中，D为参数x的可行域，由加工余量所定义的等距面距离分布控制函数g(di(x))及其上、下偏差ε和μ所定义（ε≥0，μ≥0）。当目标函数达到最小值时，得到的定位变换（R*，t*）称为最优定位变换，对应的参数x*则称为最优变换参数。

加工余量优化模型一般采用层次定位优化策略进行求解，具体可参考文献[4]。与数字化检测配准原理类似，优化后的定位变换（R*，t*）刻画了测量坐标系相对于工件坐标系的位置关系；反之，逆变换((R*)-1，-(R*)-1·t*)则刻画了工件坐标系相对于测量坐标系的位置关系，由此能够确定单个叶片或者整体叶盘的定位基准，并以约束条件同时保证加工余量的自适应优化分布。

3 基于对称原则的加工余量自适应优化

不同于单一叶片，整体叶盘的加工余量优化具有自身的特点。除了考虑叶盘的整体余量分布，单个叶片的位置及形状变化对其统一定位基准也会产生影响。因此，针对焊接式整体叶盘的工艺特性，本文从动平衡角度出发，提出基于对称原则的叶盘加工余量自适应优化方法[2]，精确度量当前焊接叶盘毛坯的方位及形状变化，实现充分改善整体叶盘运行性能的分组定位加工方式。

3.1 总体思想

叶盘加工余量自适应优化的总体思想是根据焊接毛坯的三坐标测量结果，首先判定能否采用统一的定位基准进行数控加工；若不能，按照对称的定位原则，逐层分解确定合适的叶片加工相对定位基准，即分组定位加工方式，从而在保证叶片型面误差要求的前提下尽可能地保持整体叶盘加工的一致性。

3.2 具体过程

假定叶盘的单个叶片按照上节方法能够获得优化的定位基准，并保证余量的优化分布。这里单个叶片的定位基准是指叶片相对于整体叶盘轮毂基准的位置。若无法满足此前提条件，不需做任何处理，直接判定焊接叶盘无法加工，需要采用补焊或修复的方式重新修整毛坯。

设焊接式整体叶盘毛坯的测量点集为P，设计模型为S，其中包含了M个叶片，则叶盘加工余量自适应优化的具体过程如下：

步骤1：以测量点集P与设计模型S进行余量优化建模与求解，若存在最优解，返回最优的定位变换（R＊，t＊），并建立自适应工艺几何模型S*1，退出；若否，转到下一步；

步骤2：按照对称原则提取整体叶盘的部分设计模型，并同时划分测量点集P为两个子集P1、P2，分别进行余量优化建模与求解，并判断是否存在最优解。若存在，返回最优的定位变换（）和（），并建立自适应工艺几何模型S*2，退出；若否，转到下一步；

步骤3：按照对称原则进一步分解，……，直到以整体叶盘的单个叶片毛坯作为余量优化对象，优化计算得各个叶片的相对定位基准，返回最优的定位变换（），（），……，（），并建立自适应工艺几何模型，退出。

其中，余量优化建模与求解采用上节方法；而所建立的自适应工艺几何模型，将作为数控加工的参考模型，用以估计整体叶盘的焊接变形误差。

事实上，由于焊接式整体叶盘的单个叶片变形差异较大，所以多数情况下余量自适应优化的最终结果都可能是单个叶片的独立加工。然而，在一定的公差允许条件下，寻找保持叶盘加工一致性的分组定位加工方式还是有意义的。

可以看出，叶盘加工余量的自适应优化过程充分考虑了焊接毛坯的实际误差分布特点，按照统一到逐层分解的定位方式确定了合适的叶片加工相对基准。这一过程不但满足了实际加工工艺需求，也最大程度地保证了整体叶盘运行的动平衡特性，符合实际工程背景需要。

4 算例分析

以某焊接式整体叶盘加工为例，分析并计算其余量优化的详细过程，如图1所示：该整体叶盘包含了20组叶片，图1(a)为设计模型，图1(b)为毛坯模型。为了模拟焊接变形，从其中某一叶片开始，按逆时针方向进行叶片编号，并随机施加沿叶片相对坐标系zc轴方向的旋转变换，建立焊接毛坯模型。具体的旋转角度参见表1，满足正态分布N（0，0.12）。

将毛坯模型进行等参数离散，并添加随机噪声（N（0，0.1，0.012））生成测量仿真数据，如图2所示。其中，每组叶片包含了60个测量点（叶尖：40，过渡：10，叶根：10）。

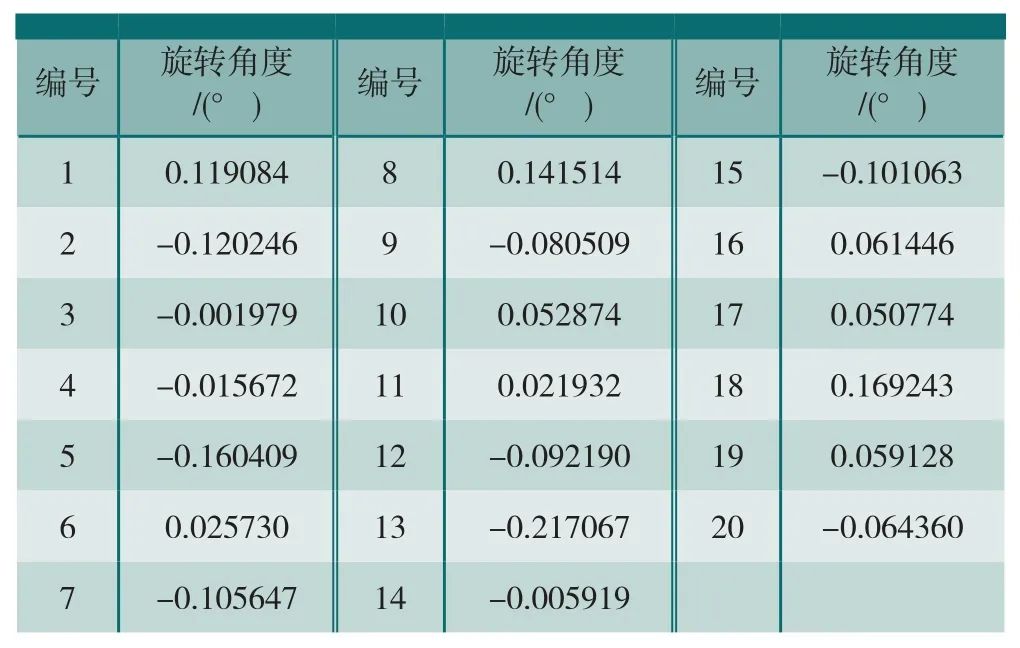
表1 焊接变形定位变换参数设置

图2 焊接式整体叶盘毛坯测量点集分布Fig.2 Measurement points for linear friction blisk blank

利用本文所提方法进行叶盘加工余量的自适应优化。针对叶盘整体余量优化求解时，迭代呈发散状态，判断不存在优化解。进而按单双编号将叶片分为两组，分别进行定位及优化，具体的迭代过程如图3、4所示。

图3 单号组叶片加工余量优化的迭代过程Fig.3 Allowance Balancing Iteration for odd group

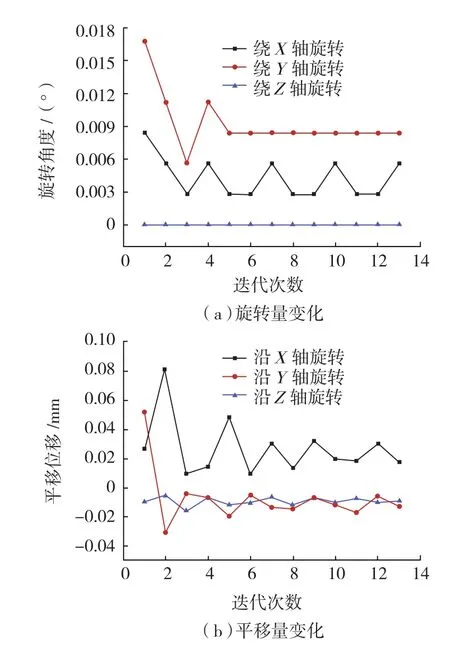
图4 双号组叶片加工余量优化的迭代过程Fig.4 Allowance balancing iteration for even group

按照两个定位基准进行焊接式整体叶盘加工，其余量的分布能够获得优化，结果如表2、图5、6所示。

可以看出，优化后的叶盘叶片相对定位基准发生了变化，叶片不同区域的有向距离误差也获得了不同程度的降低。这一结果保证减少焊接工艺引起的叶片位置偏差和余量分布不均对叶盘加工质量的影响。

5 结束语

针对焊接式整体叶盘毛坯可能存在变形、余量不均的问题，本文从动平衡角度出发，提出了一种基于对称原则的叶盘加工余量自适应优化方法。算例及分析表明：本文方法能够有效地控制焊接叶盘毛坯余量分布，确定合适的定位基准，从而降低焊接变形误差对数控加工效率、精度的影响。

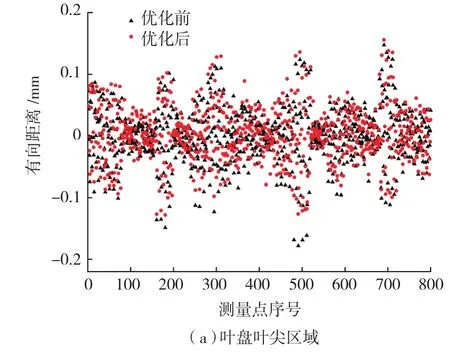
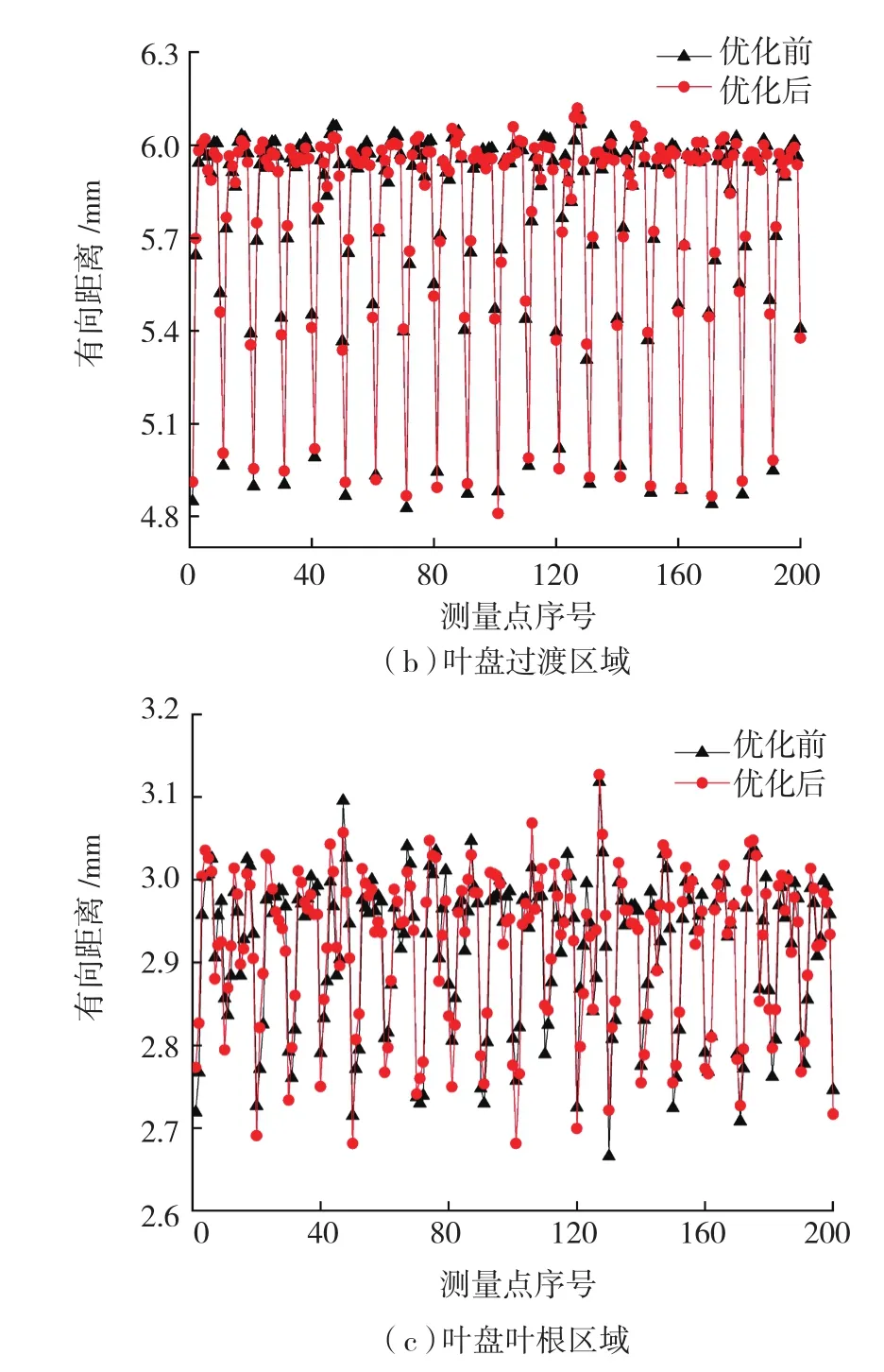
图5 余量优化前后的有向距离误差对比Fig.5 Error comparision of allowance balancing

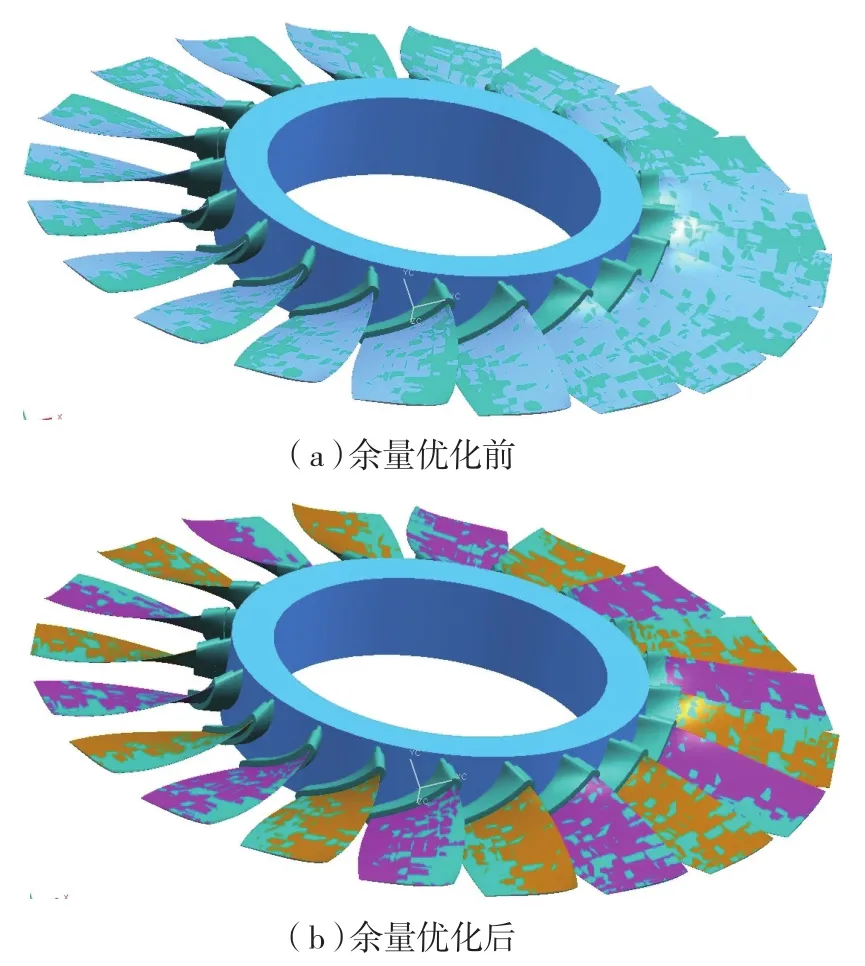
图6 余量优化前后的模型对比Fig.6 Model comparison of allowance balancing

[1] 任军学，张定华，王增强，等.整体叶盘数控加工技术研究.航空学报，2004，25(2)：205-208.

[2] 张定华，张莹，吴宝海，等.自适应加工技术在整体叶盘制造中的应用.航空制造技术，2008(13)：51-55.

[3] 史耀耀，段继豪，张军锋，等.整体叶盘制造工艺技术综述.航空制造技术，2012(3)：26-31.

[4] 张莹.叶片类零件自适应数控加工关键技术研究[D].西安：西北工业大学，2011.

[5] 王文理，袁士平.自适应加工技术在数控加工领域的分类与应用.航空制造技术，2013(6)：26-29.

[6] GAO J，CHEN X，YILMAZ O， et al.An integrated adaptive repair solution for complex aerospace components through geometry reconstruction. International Journal of Advanced Manufacturing Technology，2008，36(11-12)：1170-1179.