论向量在立体几何和平面解析几何中的应用

刘川锋

平面向量的运用作为中学数学的重要教学内容之一，具有几何与代数的双重性质，向量工具为数学问题的解决提供了新的有效方法与思路。同时向量也是中学数学课堂改革过程中的重要举措。在解决立体几何与平面解析几何问题时运用平面向量法能够帮助学生更加明晰代数与几何之间的联系，培养学生的数学思维。因此，教师应积极转变传统几何法的解题模式，贯彻“数形结合”的数学教学理念，为学生学习论证与度量问题扫清障碍。

向量立体几何平面解析几何在数学中，向量即具有方向、大小且遵循平行四边形法则的量，根据向量方向与大小的不同，可以将其分为固定向量与自由向量。将向量法应用在立体几何与平面解析几何的问题中是一种很好的思路与方法，学生通过利用向量代数的方法能够有效避免思维障碍，将逻辑推理的难度降低，利用坐标运算法及“数形结合”的数学思维提高解题效率。

1向量概述

1.1概念

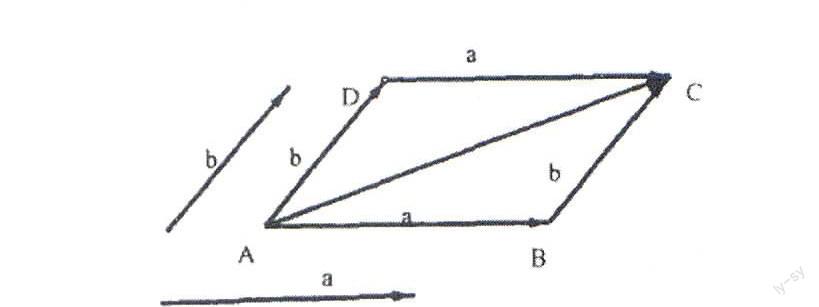
求向量差：通过将两个向量的始点重合，将减向量的终点作为始点，将被减向量的终点作为终点，两点之间的差即两向量之间的差。

1.3向量与实数的积

向量与实数的乘积仍表示向量，零向量与任何向量及实数的积均为零向量。

1.4向量的坐标运算

向量表示的有向线段的终点坐标与始点坐标的差即向量的坐标，两个向量的坐标之和则为向量和的坐标，同样的，两个向量的坐标之差就为向量差的坐标。

2平面向量法在立体几何和平面解析几何中的应用

2.1运用图形，建立数形结合思维

在解决立体几何问题的过程中，利用传统的解题方法，即综合推理法，由于立体几何中的角度、距离等问题具有较强的技巧性，需要学生具有极强的逻辑推理思维能力以及抽象的空间想象力，并且此类题目没有一成不变的规律，从而使得学生智力受到了很大考验，在思考问题时面临很大挑战。这个时候就需要运用数形结合的思维来处理这些问题。

在数学教学和实际应用中，我们都要培养学生的空间想象能力，并将这种能力应用于立体几何问题解决中去。学生建立好空间概念，画好正确的立体图形是解决立体几何问题的第一步。教师要培养学生的空间概念，可以通过制作几何课件和几何模型的方法，让学生从不同角度近距离观察并绘图，从而增强学生对立体空间的理解能力，并提高学生的作图能力。

利用平面向量法处理中学数学立体几何问题，是数学中“数形结合”思维的很好体现，平面向量法能够将立体几何中的空间问题转化为代数问题，有效避免了传统解题过程中添加辅助线等方式，削弱了抽象推理论证带来的难度，为学生提供了更加便捷、高效的解题方法。在求解立体几何中平面角的问题时，首先应分析题意判断所求的角为锐角还是钝角，然后通过计算取“相等角”或者“补角”。

在高中数学中，平面解析几何问题主要涉及圆锥曲线相关问题。由于向量具有几何与代数的双重性质，能够将几何图形的特征与代数的运算性质同时反映出来，使其成为解决平面解析几何问题的重要工具，对提高学生的自主学习与探究能力具有很好的作用。平面向量方法中体现出的数学思想与平面解析几何问题的要求十分符合，向量法作为新教材中的重要改革内容，通过利用坐标将平面向量刻画出来，以图形问题代数化的思维进行解题，使得解题方法更具操作性。

2.2转换思维，增强学生抽象化知识理解能力

思维转换是学生在学习中常常需要用到的一种学习方法，运用思维转换，可以帮助学生建立起不同知识之间的联系，在面对几何问题时，就可以充分利用这种方法，来提高学生对一些抽象知识的理解。运用向量工具能够较为容易的将一些复杂的几何问题转化，利于学生解题。

在数学平面几何问题中，点的集合形成图形，而平面图形中的点可以通过向量来表示。这样就可以把平面几何图形看作是若干向量的集合，然后利用代数运算法对平面几何中的图形位置关系进行度量。通过利用向量工具解决问题可以避免传统几何法中大量的逻辑论证过程，使得学生更容易理解抽象化的平面问题，简便解题过程。

在平面解析几何的解题过程中应用向量相等关系需注意几方面问题：在求点的坐标时应注意明确始点、终点；在利用向量坐标方法时通常采取设点而不求解的消除法进行；当存在多个解时应对各个解进行验证，避免增失根的问题。在高中数学的教学过程中，解析几何的学习是在教授了平面向量之后开展的，并不是以融合的方式进行的，这使得平面向量与解析几何的整合程度较低。但实际上向量法对解析几何问题的解决具有十分高效的作用，能够帮助学生理清思路，简洁的解题过程有助于帮助学生树立学习信心，提高兴趣。

3结束语

综上所述，在高中数学的教学过程中，立体几何问题与平面解析几何问题是重难点内容，巧妙利用平面向量法能够帮助学生提高数学思维能力，拓宽学生的数学知识，为其在解决上述两类问题提供新的解题方法与思路。同时，平面向量法的引入使得高中课堂数学内容更加丰富，教师应结合中学生的思维特征深入研究平面向量法，并与教学内容恰当结合，在新课改的要求下以简洁、优化的解题方法提高学生的逻辑思维能力与自主探究能力。

参考文献：

[1]樊玉敏.数形结合，巧学向量——《数学》第七章“平面向量”教学建议[J].江苏教育（职业教育版），2013，（10）.

[2]尹玲.抓好向量学习对学生能力的培养[J].语数外学习（数学教育），2012，（2）.

[3]丁益祥.谈平面向量的教学⑴——数学必修4平面向量部分教材分析和教法建议[J].高中数理化，2013，（16）.

[4]龚卫东.例说作图解立体几何题[J].高中数理化，2012，（9）.