以“形”解“数”三步,化解学生数学难题
2015-05-30刘保华
刘保华

【摘要】“数”与“形”是数学研究中两个最古老也是最基本的问题,我们今天所学的数学中所有的问题都是围绕着“数”与“形”的提炼、演变、发展而展开的,“数”与“形”可以说是支撑数学的两块基石.因此,在高中数学的教学中,教师可以充分利用数形结合的思想方法,引导学生化本于形、化繁为简、化隐于明,有效化解教学中的重点和难点,显著提高教学效率.
【关键词】高中数学;教学方法;数形结合
一、以“形”解“数”,具体转化抽象概念
高中阶段的数学知识相较于小学和初中来说更加的抽象和复杂,加大了学生的学习难度,因而教师在实施教学的时候要善于把抽象的数学概念和具体的图形结合起来,帮助学生在脑海中建立起概念的模型,有效化本于形.例如,在教学“空间几何体”时,数学教师可以自己制作简单的Flash动画,通过演示矩形、直角三角形、直角梯形绕一边旋转的过程,让学生亲眼见证其形成圆柱、圆锥、圆台,使“把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体”这一旋转体的定义跃然纸上,成功帮助学生突破二维平面进入三维空间.接着就是“空间几何体的三视图”,其教学也可以通过多媒体的演示来轻松实现:教师先将一个圆锥进行旋转、翻转等,向学生全方位展示圆锥的各个面,从视觉上对“三视图”有一个初步的认识.然后,再让学生们把自己刚刚所观察到的圆锥在不同观测角上的“样子”画下来,从而过渡到了“三视图”的画法教学上面,提升了教学的有效性.像这样运用恰当的图形把数学概念中最本质的属性演示出来,使学生能够更为直观地认识到该概念的实际意义,从鲜明的表象中抽象出深刻的内涵,建构数学概念,比起教师的长篇解说更容易理解,也更为有趣.所以高中数学教师要有意识地将抽象概念转化为具体形态,帮助学生建构表象,促进感性认识上升为理性认识.
二、以“形”解“数”,清晰梳理数量关系
数量关系是解数学题的关键所在,只要理清了题中的数量关系,问题基本也就迎刃而解了.但在教学过程中,教师要十分重视对数量关系的梳理,有效利用“数形结合”的方式创建教学情境,帮助学生理清数量关系.例如,在引入“函数”这一单元的内容时,由于学生是第一次开始接触“函数”这一新知识,难免会产生一些心理上的恐惧感,为了使他们迅速进入学习状态,建立学习的信心,教师在讲“生活中的变量关系”这一节中就应该制作生动形象的课件来演示变量之间的关系.比如路程与时间的正比关系,就可插入“龟兔赛跑”的动画来向学生表示:一声枪响,乌龟和兔子从同一起点同时出发,视频中用红线和黄线分别把乌龟和兔子的运动轨迹表示出来,所以学生们可以明显地观察到黄色的轨道在迅速地变长,相对而言红线却迟迟不见增长.同时,课件的右上角还挂了一个秒表,来让学生注意到时间的推移.接着,教师就可让学生列出视频中总共有哪些“数量”,并说一说它们之间的关系,讨论分辨出“自变量”和“因变量”.在后续的讲课过程中,教师还可再插入播放一段烟花在空中绽放的视频,以此告诉学生函数图像就像是烟花一样有起有落,让学生从“形”上感知函数、发现函数,在轻松的心理状态下进行数学知识的学习.以这样的生动具体的形式将数量之间的关系清晰地演示出来,成功地把抽象叙述转化为了直观呈现,从而达到化繁为简、帮助学生理清数量关系的目的.
三、以“形”解“数”,巧妙凸显数学规律
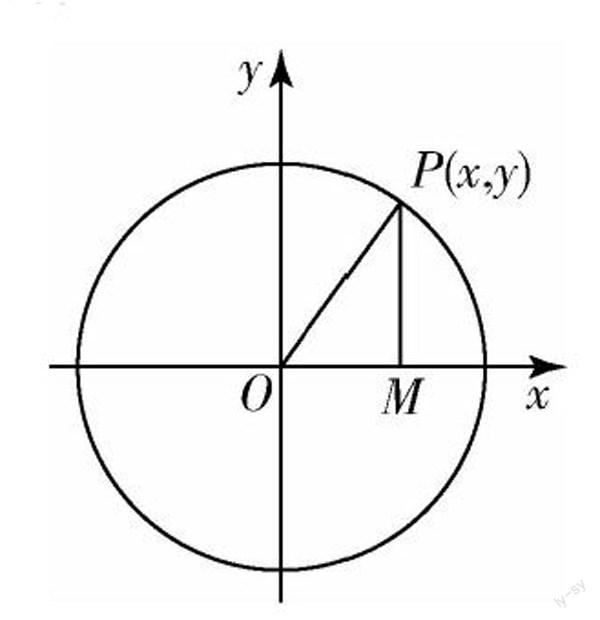
数学规律总隐藏于现象之中,要从现象中概括出普遍规律对于学生来说不是一件容易的事情.所以数学教师要把“数”和“形”结合起来,帮助学生总结事物规律.借助单位圆来教学“任意角的三角函数”这一课,首先引入锐角三角函数在单位圆中的定义(如右图),利用点P的坐标和之前所学的知识,得出sinα=yx2+y2,cosα=xx2+y2,tanα=yx,并化简为sinα=MPOP=y,cosα=OMOP=x,tanα=MPOM=yx.接着,再以此为基础把P点的位置(角的终边与单位圆的交点)移动到第二、三、四象限的对应位置,学生依葫芦画瓢很快就能写出相应的函数.
这是利用以“形”解“数”的方法让学生发现其中所蕴含的规律,从锐角三角形函数推出任意角的三角函数的例子,实践证明这个方法是非常有效的.另外,我们还可以利用“六边形记忆法”来帮助学生记忆三角函数的八大关系,如右边图形结构所示:“对角线上两个函数的积为1.阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方.任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积.”
并教给学生“上弦中切下割,左正右余1中间”的口诀,大大提高了记忆的效率.这不仅成功将数学规律凸显出来,降低了学生理解和记忆的难度,也给学生们提供了一种高效学习的方法,在一定程度上提升了学生的自主学习能力.
四、结束语
“数”与“形”作为数学学习的两条主线,是教师在教学中必须要把握的关键.高中数学的内容较为艰深,教师要认真备课、积极研究,把教材中的“数”与学生熟悉的“形”巧妙结合起来,为高中数学的课堂教学注入生机与活力.也只有这样,才能帮助学生们逐渐建立起学习数学的自信心,提高教学的效率.
