基于压缩感知的混沌成像雷达
2015-05-30唐骏张璘袁江南
唐骏 张璘 袁江南
【摘要】 匹配滤波器常用于雷达接收端,在宽带雷达中,这会导致系统复杂且成本高昂。利用压缩感知可以不用匹配滤波器和高速模数转换器,且能实现高分辨雷达成像。鉴于雷达目标场景的稀疏性,提出一种用于混沌雷达的压缩感知方法,用Bernoulli映射生成混沌调频信号,利用该信号的随机性,直接构造观测矩阵。通过优化技术,可以由欠采样的回波信号重构雷达景象。仿真了静态和非静态目标雷达景象,与匹配滤波处理相比,所提方法不仅处理简单,且性能更优。结果验证了该方法的可行性。
【关键词】 混沌雷达 宽带雷达 压缩感知 匹配滤波器
一、引言
高分辨雷达成像技术对于雷达目标识别和特征提取具有重要意义,由雷达成像原理可知[1,2],目标的距离向分辨率取决于发射信号的带宽,方位向分辨率取决于相参积累时间。受Nyquist采样定理的约束,传统宽带雷达成像系统面临着采样率高、数据量大、回波数据有限等诸多问题。
压缩感知(compressed sensing, CS)[3-7]理论为宽带雷达成像提供了一种新途径。该理论表明,对于具有稀疏性的信号,通过少量次数的观测,即信号的投影值就能精确或近似重构原信号。对雷达目标电磁散射特性的研究结果表明[8],高频区雷达目标脉冲响应可由少数重要散射中心来刻画,宽带雷达能得到的重要散射中心数远小于识别这些散射中心所需的样本数。除了压缩感知,雷达信号的选择直接影响距离-多普勒成像系统的性能。混沌信号用于雷达系统有许多独特的优点,它们表现出随机噪声特性,具有频带宽、易产生等特点[9]。另一方面,频率调制信号有高的成像分辨率,高输出功率,低成本与低截获、干扰概率等优点。
二、压缩感知
压缩感知理论出现在2000年左右,在随后的几年中得以迅速发展。CS 理论主要涉及三方面:信号的稀疏表示、信号的非相关采样和信号的精确重构[10]。
2.1观测矩阵

2.2重构算法
重构算法是指用低维的观测信号y精确重构高维原信号x。目前,重构算法主要分为3类: 1) 基于l1范数的凸优化算法;2) 基于l0范数的贪婪算法;3) 组合算法。本文采用凸优化来重构雷达景象。凸优化方法是基于l1范数最小进行求解,相比于其它算法,重构效果较好。
三、基于压缩感知的混沌成像雷达
压缩感知的混沌雷达系统框图如图2所示,混沌序列经频率调制之后作为雷达发射信号,同时用来构成观测矩阵,接收的回波通过与观测矩阵运算得到观测信号,利用优化算法,由观测信号重构雷达景象。
混沌信号具有随机噪声的特征,自相关函数近似于δ函数,互相关函数近似为0,从上世纪九十年代开始,许多学者对混沌在雷达信号设计中的应用开展了研究,证明了混沌应用于雷达信号设计的可行性。研究内容集中在两方面:混沌相位编码信号和混沌调频信号。在采用混沌序列进行调频时,只有用Bernoulli映射产生的序列才能得到较理想的自相关特性[13],因此本文用Bernoulli映射产生混沌序列,式(7)用来产生Bernoulli序列
四、仿真及结果分析
4.1静态目标仿真
雷达发射信号与目标卷积得到回波信号,为了用矩阵相乘来表示卷积运算,通过将混沌调频信号S[n]移位来形成矩阵各列,由于混沌调频信号具有类似噪声特性,此矩阵在基于压缩感知的混沌雷达系统中可用作观测矩阵。
对于静态目标,目标参数主要包括距离和散射系数,通过随机放置具有不同散射系数的物体来模拟雷达景象,如图5所示,其中横坐标表示目标到雷达的距离,纵坐标表示目标的散射系数。仿真时,为了应用压缩感知,观测的信号应少于卷积结果的样点数,可以通过下采样观测矩阵来实现。对于压缩感知,观测矩阵的各列需满足不相关性。下采样后的观测矩阵各列的相关性如图6所示。
对于静态目标,雷达景象通过2.2节中所说的凸优化技术来重构,如图7所示,可以清晰看出,用压缩感知,由欠采样的样点可以精确重构雷达景象。另外,图8是利用匹配滤波器恢复的雷达景象。可以看出,匹配滤波器在恢复雷达景象的同时引入了许多噪声,而且要求从回波中获得足够的样点。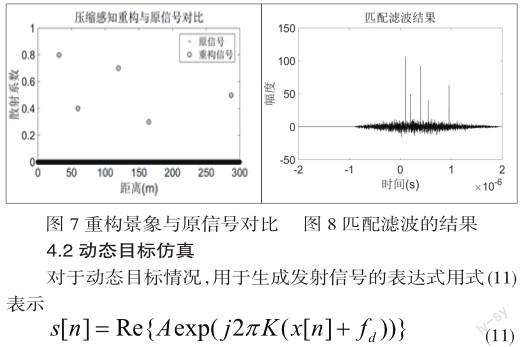
其中A是信号幅度,K是调制指数,x[n]是混沌函数的离散形式,fd是多普勒频率。用于生成Bernoulli序列的参数与静态目标情况相同。如前所述,生成的混沌调频信号需要重排以形成观测矩阵。与静态目标情况不同,对于非静态目标,每一个多普勒频率需要移位所有距离维信号以形成观测矩阵,如图9所示。
对于动态目标,目标的参数主要包括距离和多普勒频率,可以用二维平面上的点来模拟,其中横坐标表示距离,纵坐标表示目标的多普勒频率。通过随机放置目标生成二维的景象图,如图10所示。为了应用压缩感知,景象图需要化为一维矢量。该矢量表示,对于每一个多普勒频率,重复所有可能的距离。图10矢量化后的结果如图11所示,图10景象图为100行、100列,化为一维矢量即长度为10000。

跟静态目标情况一样,为了应用压缩感知,观测矩阵与接收信号需要下采样。在接收端,通过凸优化技术重构雷达景象,如图12所示。图13是压缩感知重构与原信号的对比图。图14是用匹配滤波器恢复的雷达景象。可以看出,匹配滤波器引入了大量的噪声,这些干扰可能会掩盖目标或很难区分靠得近的目标。
五、结束语
提出了一种用来提高混沌雷达分辨率的压缩感知方法。用Bernoulli映射生成的混沌序列经调频后用作发射信号,该信号具有类随机噪声特性,其模糊函数近似于“图钉”形,且可直接用来生成观测矩阵。仿真了静态和非静态目标雷达景象,与匹配滤波法进行了比较。对于静态目标,雷达景象包含了目标的距离和散射系数,回波信号通过观测矩阵后下采样,应用优化技术,从下采样的接收信号中可以恢复雷达景象。与匹配滤波法相比,压缩感知所需数据量小,抗噪声性能好。对于非静态目标,雷达景象包含了目标的距离和速度。该情形下,匹配滤波器虽然能够恢复雷达景象,但同时引入了许多噪声,使得目标难以辨识。相比之下,即使接收信号下采样,压缩感知也能精确恢复雷达景象。仿真结果表明,基于压缩感知的混沌雷达系统结构简单,无需匹配滤波和高速的模数转换器,数据处理量小,十分适用于宽带高分辨雷达的应用。
参 考 文 献
[1] Richards M A. Fundamentals of Radar Signal Processing [M]. Second Edition, McGraw-Hill Education, 2014.
[2] Mahafza B R. Radar Systems Analysis and Design Using MATLAB [M]. CRC press, 2000.
[3] Donoho D L. Compressed sensing [J]. Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306.
[4] Malloy M L, Nowak R D. Near-optimal adaptive compressed sensing [J]. Information Theory, IEEE Transactions on, 2014, 60(7): 4001-4012.
[5] Candès E J, Wakin M B. An introduction to compressive sampling [J]. Signal Processing Magazine, IEEE, 2008, 25(2): 21-30.
[6] Gangopadhyay D, Allstot E G, Dixon A M R, et al. Compressed sensing analog front-end for bio-sensor applications [J]. Solid-State Circuits, IEEE Journal of, 2014, 49(2): 426-438.
[7] Zhang Shun-sheng, Zhang Wei, Zong Zhu-lin, et al. High-resolution Bistatic ISAR Imaging Based on Two-dimensional Compressed Sensing [J]. Antennas and Propagation, IEEE Transactions on, 2015, 63(5): 2098 -2111.
[8] Wang Li-bo, Tan Yun-hua. A Novel Approximate Solution for Electromagnetic Scattering by Dielectric Disks [J]. Geoscience and Remote Sensing, IEEE Transactions on, 2015, 53(5): 2948-2955.
[9] Yang Qi-lun, Zhang Yun-hua, Gu Xiang. Wide-Band Chaotic Noise Signal for Velocity Estimation and Imaging of High-Speed Moving Targets[J]. Progress In Electromagnetics Research B, 2015, 63: 1-15.
[10] 徐建平. 压缩感知算法在雷达成像中的应用研究 [D]. 电子科技大学, 2012.
[11] Candès E J. The restricted isometry property and its implications for compressed sensing [J]. Comptes Rendus Mathematique, 2008, 346(9): 589-592.[12] 张磊, 柏业超, 张兴敢. 压缩感知在宽带雷达信号处理中的应用[J]. 南京大学学报: 自然科学版, 2014, 50(1): 35-40.
[13] Flores B C, Solis E A, Thomas G. Chaotic signals for wideband radar imaging [C]//AeroSense 2002. International Society for Optics and Photonics, 2002: 100-111.
