夯实基础?提升能力

周新伟?吴利华

现在的高考侧重考查学生的基本知识、基本技能和基本方法，其中对能力的考查尤为重要。这些要求也成就了高三数学一轮复习的要求：重点是基础， 指导思想是全面、系统、扎实、灵活。通过一轮复习，学生需要掌握基本概念、性质、定理及其一般应用。一轮复习过程除了有简单的知识回顾，还有大量的题目训练，如何从各个环节入手，全面复习，让学生经过一轮复习后对概念的理解更全面、更深刻，同时拥有类题辨析能力，对一些存在的问题轻松地解决和击破，避免收效甚微的题海战，就成为摆在我们面前的大问题。

一、 注重概念的回顾

概念是对某知识的描述，这种描述包含了此知识的特征、特性、使用的条件等，对概念的深刻理解是一切数学活动的基础。对概念的回顾，不仅是陈述概念的内容或是指出关键字，而且是对概念的正确理解和灵活运用。我们只有对概念充分理解，才能深入了解数学的本质，一些改头换面的题目才能迎刃而解。因此在一轮复习中对概念的回顾不能草草了事。

例1：已知函数f（x）=x+lnx，g（x）=1+lnx，h（x）=ex+x的零点分别为a，b，c，则a，b，c的大小关系？

问题分析：当这道题出现在练习中时，很多同学表现出一种无所适从的状态，分析发现，产生障碍的主要原因还是因为概念不清晰，即何为零点，书中为零点的判断提供了什么依据。教材在必修1（P74～P75）明确了零点的概念：我们把使函数y=f（x）的值为0的实数x称为函数y=f（x）的零点。此外，书中还有我们俗称的零点存在性定理：一般的，若函数y=f（x）在区间[a，b]上的图象是一条不间断的曲线，且f（a）·f（b）﹤0，则函数y=f（x）在区间（a，b）上有零点。结合起来，我们可以总结出零点判断的三种方法：①算（求出零点）；②看（看图象上两函数的交点），③验（用端点进行验证）。这三种方法可以恰如其分地用于本题三个零点的判定大小上。

可见，对概念不仅仅是记住，更重要的是理解和运用。教师在给学生复习概念时，一方面复述其内容，强调关键语句，另一方面要借助于例题帮助学生理解概念的实质含义，引导学生正确地使用。

二、注重书本习题的开发、引申、整合

例2：必修4——P83：已知直线l经过点P1（x1，y1），P2（x2，y2）用向量方法求l的方程。

必修4——P84，第8题（阅读题）： 设P1（x1，y1），P2（x2，y2）为直线上两点，则向量P1P2及与它平行的向量都称为直线的方向向量。当直线与轴不垂直时，—P1P2，即（1，k）也是直线的方向向量，其中k是直线的斜率。

如果直线经过点P1（x1，y1），且它的方向向量是（1，k），试用向量共线的方法推导直线的点斜式方程。

必修4——P87：在解析几何中我们学习了直线方程，知道Ax+By=0表示平面内一条直线l，若将直线方程写为向量的坐标运算形式，便有（A，B）·（x，y）=0，其中（x，y）表示直线l上任一点M的坐标，也即向量OM的坐标。令n=（A，B），则n⊥OM。我们把与直线l垂直的向量称为直线l的法向量，故n=（A，B）是直线Ax+By=0的一个法向量。令v=（-B，A），因为v·n=（-B，A）·（A，B）=

0，所以v⊥n。也就是说，v=（-B，A）是直线Ax+By=0的一个方向向量（参见习题2.5第8题）。据此式分别求出直线x+y=0及y=kx（k≠0）的一个法向量和一个方向向量。

必修2——P106第7题：已知圆C的方程是x2+y2=r2，求证：经过圆C上一点M（x0，y0）的切线方程是x0x+y0y=r2。

整合后，以书中的例题作为引论，引出了以向量作为背景的题：

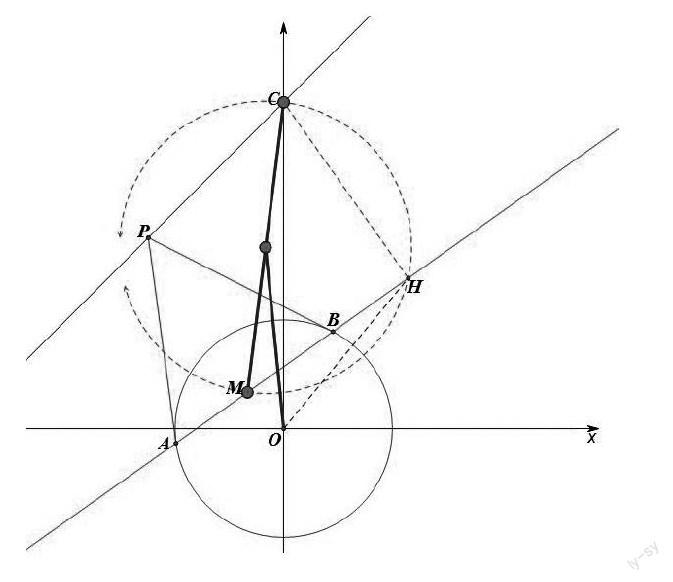
例3：点P是直线l：y=x+3上任意一点，过点P引圆O：x2+y2=1的两条切线，切点分别为A（x1，y1）、B（x2，y2），点C（0，3）在直线AB上的射影为H，求OH的最大值。

三、注重易错题的整理

易错题的整理是每个高三学生都会去做的工作，做这样的工作可以弥补在知识上的缺漏，也是对自己容易犯的错误起到一个提醒的作用。但这个过程如果仅仅靠学生进行，我们往往会看到错题本“内容丰富，毫无章法”，容易使错题本“流于形式”，甚至出现错题本上的问题本身就是错的。所以老师的引导和参与在一定程度上也是需要的。

第一，加强检查。通过检查可以督促学生的完成；第二，加强老师的指导，老师可以就某一部分提出整理要求，要求学生对错题进行分类、整理、变式、延伸，也可以就在整理过程中出现的优秀同学的整理做出点评，给出示范，在错题整理时可以加入错因分析等；第三，加强同学间的沟通，同学间错题的共享可以让学生引以为戒。

对个别学习困难的学生，还要进行一些单独的辅导，要求学生将易错题（仅仅是题目）摘抄，两个星期或更长的时间之后再订正，若订正错了，再重复以上步骤，直到订正对为止。这样能学生的错题越来越少，知识点越来越清晰，各方面的能力越来越得到提高。

笔者在教学过程中曾把经典错题整理后对个别学生进行辅导，成效显著，也避免学生花费太多时间和精力面对众多习题无所适从。

四、注重习题讲解的策略

同样的教案，不同的上课形式（或者说上课风格），显然也会产生很大差异的教学效果。不同的教学方式是产生差异的主要因素，比如，是讲解还是练习？是讲多还是讲少？是讲快还是讲慢？是口述还是板书？这需要教师在习题讲解中注重讲解的策略。

1.先宏观，再微观

一轮复习上课时有时需要向学生先作宏观说明，如章节结构框架或本课主题。

以代数函数为例，可向学生作如下说明，中学阶段主要有十大函数（三角函数暂不列其中）：一次函数、二次函

数、三次函数、幂函数、指数函数、对数函数、反比例函数及一次分式函数（平移可化为反比例函数）、“双曲线型”函数（y=ax+—）、绝对值函数（一个或多个和与差）、无理函数（一个或多个和与差）。由此十大函数当然还可变化出综合形式的函数，如绝对值与其他函数相结合而形成的新函数，对数函数、指数函数与一次、二次、分式等函数结合形成的新函数。学生只有在整体上认识到各知识点结构，才能纲举目张。若对以上每一种函数，都能掌握一些典型的例题，则可使學生在宏观上认识初等基本函数。

例4：函数y=xex（x≤1）的值域为_________。

此题学生往往不能正确画图，因而导致答案出错。

求导已根深蒂固地根植于学生脑海中，求导的作用是什么？只刻画函数单调性，而函数的正负性、渐近线等都是学生容易忽视的地方。

通过宏观结构上的认识，再用一些典型的问题进行训练，就能帮助学生建立知识结构上的框架，避免犯一些低级错误。

2. 先具体，再抽象

如以下问题。

例5：函数y=—（ab≠0）的值域为___________。

一开始就让学生研究这样的问题，一是学生不感兴趣，觉得很难；二是学生也不知从何处入手，尤其是基础差的学生，备课中，不如从具体情况出发。

（1）函数y=—的值域为___________；

（2）函数y=—的值域为___________；

最后，作总结，一般的，函数y=—（ab≠0）的值域为________。

这样的模式，既调动了学生的积极性，使学生觉得轻松，自然地掌握所学知识，又提升了学生研究一般问题的总结能力。

3.先解决，再优化

很多问题常有多种解法，教师要通过适当分析，将学生在基础年级学到的各种方法加以初步对比，使学生隐约认识到不同情境下不同的最佳解题方案是什么，培养学生“高瞻远瞩”的能力，更要关注解决问题的通性通法。

例6：已知奇函数f（x）的定义域为R，且f（x）在[0，+∞）上为增函数。当0≤θ≤—时，是否存在这样的实数m，使f（cos2θ-3）+f（4m-2mcosθ）﹥

f（0）对所有θ∈[0，—]均成立？若存在，求所有适合条件的实数m，若不存在，说明理由。

此题在解决过程中利用单调性去掉f后换元，令t=cosθ，t∈[0，1]得到t2-mt+2m-2﹥0。很多学生没有任何思考直接考虑二次函数，讨论对称轴的位置，计算比较复杂且讨论的情况有三种，而此题若考虑分离参数，则非常简单。学生在一轮复习中解决问题不能只是解决了就好，要指导学生注重审题，注重计算，注重细节，让学生学会在解题中一题多变、一题多解，注重方法的优化、运算的优化，培养数学思维的能力。

五、注重学法指导及心理辅导

及时收集学生在学习数学过程中的困惑，学生的困惑如果积累得过多可能会使学生产生对学习数学的恐惧心理，从而影响学生数学的学习。教师只有平时及时解答学生的困惑，及时鼓励，才能使学生学习数学的热情持续下去。教师要鼓励学生认识自己，不论是平时做作业还是高考复习中的定时练习、模拟考试，做完后要认真改错，通过对自己在练习中出现的错误的纠正，使自己的能力得到提高。平时坚持认真改错，能力提高得快；反之则练习效果差，能力提高得慢。因此，我们说“错误是最好的老师”，在复习中要利用好曾经做错过的题目，寻找错因，及时进行总结，以吸取教训，力求相同的错误不犯第二次。

教学中要注意分层教学。针对不同学生的实际水平，合理安排教学难度，有利于学生产生成功情感体验，提高学习水平。

在复习过程中，难免会出现一些大大小小的失误，也会遇到一些大难题，这时候，要么束手无策，要么费了九牛二虎之力才能解决，要么问题虽然解决了，但自我感觉不好。 碰到这种情况不要紧张，不要轻易放过。数学问题博大精深，数学对每个学生来说都会有一定难度，所以要培养学生较强的心理承受能力，鼓励学生勇往直前。同时还要注意辅导学生在考场上保持较好的心理状态。

引导学生共同探讨，形成“独乐乐不如众乐乐”的学习数学的氛围。在教学过程中，有意识地让学生参与到教学中来也能取得意想不到的效果。

总之，高三数学一轮复习是一项巨大的工程，以上的各个环节都要认真、细致地实施。经过一轮复习，学生不仅能回顾基本知识，还能将知识不断深化，理清知识之间的关系，逐步形成结构体系，掌握解题的基本方法，最终实现全面提高解决问题的能力，从而达到夯实基础提升能力的效果。

（作者单位：江苏省無锡市天一中学）