常见不等式通用解法的一般步骤

唐勇

【摘要】 不等式的解法是中学数学的主体内容，几乎覆盖了高中数学所有的章节. 常见的不等式包括一元二次不等式、一元高次不等式、分式不等式及带绝对值的不等式，针对这几类不等式，我们从中寻找出一种通用的解题方法，使问题化难为易、化繁为简，从而得到顺利解决.

【关键词】 一元二次不等式；一元高次不等式；分式不等式；带绝对值的不等式；通用解法

解一元二次不等式、一元高次不等式、分式不等式和带绝对值的不等式的一般步骤：

1. 变形（将不等式的最高次项系数变成正数；带绝对值的不等式应变形成|x| > a或|x| < a （a > 0）的标准形式）

2. 求根（解出不等式所对应的方程的实数根）

3. 标根（将实数根依次表示在数轴上）

4. 穿根（用一根曲线从右往左、自上而下分别穿过方程的每一个根，一个根穿一次）

5. 取区间（变形后的不等式如果是“>”，取数轴上半部分曲线所对应的区间；如果是“<”，取数轴下半部分曲线所对应的区间）

例1 解不等式-3x2 + 5x + 2 > 0.

解 先将不等式变形为：3x2 - 5x - 2 < 0.

该不等式所对应的方程为：3x2 - 5x - 2 = 0，

解出方程的实数根：x1 = 2，x2 = -■.

所以不等式-3x2 + 5x + 2 > 0的解集为-■，2.

例2 解不等式■ ≤ 0.

解 将不等式变形为：■ ≥ 0.

该不等式所对应的方程为：■ = 0，

解出方程的根：x1 = ■，x2 = -3，x3 = 4.

所以不等式■ ≤ 0的解集为：-3，■∪（4，+∞）.

例3 解带绝对值的不等式3 > |2x + 7| - 10.

解 将不等式变形为：|2x + 7| < 13.

该不等式对应的方程为：|2x + 7| = 13，

解得：x1 = 3，x2 = -10.

所以不等式3 > |2x + 7| - 10的解集为：（-10，3）.

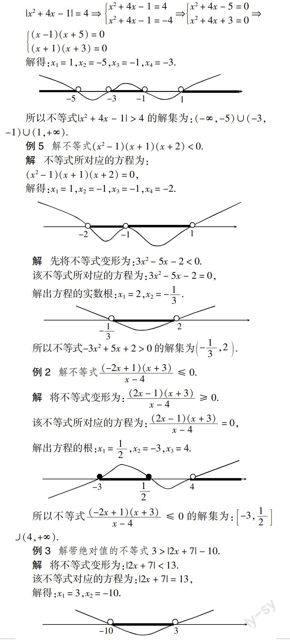
例4 解带绝对值的不等式|x2 + 4x - 1| > 4.

解 由于该不等式已经是标准的带绝对值的不等式，所以不用变形，直接解其对应的方程，过程如下：

|x2 + 4x - 1| = 4 ？圯 x2 + 4x - 1 = 4x2 + 4x - 1 = -4？圯x2 + 4x - 5 = 0x2 + 4x + 3 = 0？圯

（x -1）（x + 5） = 0（x + 1）（x + 3） = 0

解得：x1 = 1，x2 = -5，x3 = -1，x4 = -3.

所以不等式|x2 + 4x - 1| > 4的解集为：（-∞，-5）∪（-3，-1）∪（1，+∞）.

例5 解不等式（x2 - 1）（x + 1）（x + 2） < 0.

解 不等式所对应的方程为：

（x2 - 1）（x + 1）（x + 2） = 0，

解得：x1 = 1，x2 = -1，x3 = -1，x4 = -2.

所以（x2 - 1）（x + 1）（x + 2） < 0的解集为：（-2，-1）∪（-1，1）.

注 方程中相同的根叫作重根，如果是奇数个重根叫奇重根，偶数个重根叫偶重根，解不等式穿根时按“奇穿偶回”的原则.