微调细节 彰显活力

陆军

人教版义务教育课程标准《数学》教材四年级上册第81，82页“笔算除法”一课，是两、三位数除以整十数，商是一位数的笔算除法. 教材通过例1、例2分不同图书的两个情境，把笔算除法教学放置于解决实际问题之中，通过摆小棒、分方格突破难点——确定商的位置. 这一内容，是在学生已经掌握了除数是一位数的除法笔算方法以及除数是整十数的口算、估算除法的基础上进行教学的.

我校教研组确定此课为集体备课、磨课的内容. 笔者参与后，把两次教学过程及思考简单整理，与大家交流.

首次教学：大气沉闷

【课堂实录】

1. 创设情境，提出问题

多媒体出示课本主题图和信息：图书室有92本连环画，每班需要30本.

师：你能提出什么问题？

生1：可以分给几个班？

2. 合作探究，解决问题

师：请同学们独立解决. 生独立尝试后汇报.

生2：我用估算，92 ≈ 90，92 ÷ 30 ≈ 3（个）.

生3：我用口算，92 ÷ 30 = 3（个）……2（本）.

师：你不但知道了分给几个班，还知道剩下的本数. 真了不起！有没有用竖式来计算的？

生4：我用竖式笔算（师板书）：

师：你们同意吗？

生5：不同意，商“3”应该写在个位上. 因为“3”写在十位上表示30，30 × 30 = 900，被除数只有92，不够减.

师：说得真好. 理解暂时有困难的同学来看看小棒图（多媒体出示课本小棒图）.我们把92本连环画用小棒来代替，谁能通过分一分小棒来说明他的意思？

生6：3捆一堆，每堆30根，分3堆，还多2根，所以商3应写在个位上.

师：这就是我们今天要重点研究的笔算除法. （板书课题）请大家试着做一做.

生独立练后4生板演：

题1生7： 题2生8： 题3生9： 题3生10：

师：比较生9和生10，哪题对？为什么？

生11：生10对，生9错.

生12：生9把商“4”写在十位上了，表示40，40×30=1200，被除数只有140，不够减了，所以错了.

师：比较题3和题1，2，有什么区别？

生13：题3被除数是三位数，题1，2被除数是两位数.

师：三位数除以两位数该怎样做？同桌讨论.

生14： 14除以30不够除，要140除以30.

师：被除数前两位不够除，看前三位. （板书）你觉得笔算除法要注意什么？

生15：商的位置不能写错.

生16：余数一定要比除数小.

3. 巩固拓展，应用新知

多媒体出示：

（1）（ ）里最大能填几. （口答）（题略）

（2）用竖式进行计算（实物投影学生的竖式计算过程，师生评议）（口答）（题略）

（3）在运动会期间，体育老师去商场买球，篮球80元/只，排球50元/只，足球30元/只，用200元钱，如果只允许买一种，你想买什么？能买几个？还剩多少元？（生口算解决）

（4）拓展题：用尽可能多的方法解决.

生：（无应答）

师：这题请同学们课外继续思考解决. 笔算除法内容很丰富，今天只开了头，以后同学们会学到更多！

【思考一】

课后，我们反复琢磨着本课教学的得失，感悟到，上述教学流程折射出不少亮点：

1. 数学来自生活，数学回归生活

“数学来自生活，回归生活”是新课程倡导的核心思想之一. 教师通过“主题图（含例1）”“尝试练习（含例2）”“巩固拓展”三个板块的师生互动，形成了从“生活中的数学”抽象出“纯数学”，又回归“生活中的数学”的课堂教学主线. 让学生明确学习数学是为了解决生活中的实际问题，感知数学来自生活，激发探究欲望. 引导学生明确算理，领悟算法，掌握基础知识，形成基本技能. 让学生感悟学以致用.

2. 把握学习起点，体现策略多样

两道例题的教学都是以学生原有知识经验为起点，让学生尝试在前，教师点拨在后. 学生用了估算、口算和笔算解决例1，体现了策略多样化，而且真实地暴露了学生在建构新知过程中的认知错误点：将商“3”写在十位上，教师就此组织学生进行了较有效的思辨.

3. 学生尝试在前，教师点拨在后

用竖式笔算时，商的定位是本课教学重点. 两道例题的教学中，教师都采用让学生先尝试用竖式笔算，然后让学生4口头汇报，教师板书或学生板演的方法，利用学生的错误：商写在十位上，让其他学生找出错误，最后用分小棒的直观教学方法，帮助学生理解商写在个位上的算理. 这一系列的师生交流，生生互动，处处让学生走在前面，教师在后面引导、点拨，把课堂生成的错误资源当作学生探究学习的宝贵财富，凸显了新课程提倡的师生观——“学生是数学学习的主人，教师是学习活动的组织者、引导者、参与者.”这就是原生态的课堂，大气的课堂.

在扫视亮点的同时，我们发现一些细节上的缺失，制约着本课教学的实效.

1. 课始直接让学生独立尝试解决例1，学生固然用估算、口算、笔算解决了问题，但把三种计算方法放在同等地位，而且只有少数学生亲历了用竖式计算的过程，致使教学重点被淡化.

2. 引导学生得出“三位数除以两位数，被除数前两位不够除，看前三位”这个结论时欠顺畅，学生理解不够透彻. 原因是学生只经历了一道尝试题的计算，体验不够充分.

3. 第三个环节中的第（3）题，学生可以用口算解决，思维容量小，与本课教学目标不合拍. 第（4）题开放度过大，学生在课堂上无从着手，收效低.

通过上述思考，我们在保留原来基本思路的基础上，对此课的三处细节进行了微调，再次进行尝试.

再次教学：精细活泼

【片段实录一】 教学两位数除以整十数

呈现例1后，师：谁来说说自己的解决方法？

生1：我用估算 92 ≈90 92 ÷ 30 ≈ 3（个）

生2：我用口算 92 ÷ 30 = 3（个）……2（本）

师：这名同学不但知道了分给几个班，还知道剩下的本数. 真了不起！刚才同学们用到了估算和口算的方法来解决，数学中还有一种基本的计算方法——笔算. 今天我们就要一起来研究笔算除法. （板书课题）根据你的经验，92 ÷ 30应该怎样来笔算，请大家试一试.

全体学生独立用竖式尝试笔算后，师指两生板演：

生3： 生4：

师：商“3”究竟应该写在哪一位上？为什么？请在四人小组内讨论. ……

【片段实录二】 教学三位数除以整十数

[三道尝试题 的教学过程同第一次，但加上了借助多媒体演示课本中的方格图，帮助学生理解算理. ]

师：这样的三位数除以两位数你也会做了吗？请你再试一试：

学生独立尝试后，两生板演.

师：我们已经做了6道笔算除法计算题，后面三题与前面三题有什么不同？

生5：后面三题是三位数除以两位数，前面三题是两位数除以两位数.

师：为什么这6题的商都是一位数？同桌讨论.

生6：因为后三题被除数百位和十位不够除，连个位也看进去了，所以商只有一位数了.

生7：因为后三题被除数前两位不够除，要看前三位，所以商只有一位数了.

师：说得真好！老师把你的发现写在黑板上. 板书：被除数前两位不够除时，要看前三位.

【片段实录三】 巩固拓展，应用新知

（3）为参加体艺“2 + 1”活动，四年级三个班各带320元去商场买球. 篮球78元/只，排球40元/只，足球70元/只.

四（1）班买排球，可以买多少个？

四（2）班买篮球，大约可以买几个？

四（3）班买足球，能买几个？还剩多少元？

生8： 四（1）班320 ÷ 40 = 8（个），用口算.

生9：四（2）班320 ÷ 78 ≈ 4（个），用估算.

生10：四（3）班320 ÷ 70 = 4（个）……40（元），用笔算.

师：解决了这个问题，你有什么想法？

生11：我知道了根据不同的需要，我们可以采用不同的计算方法.

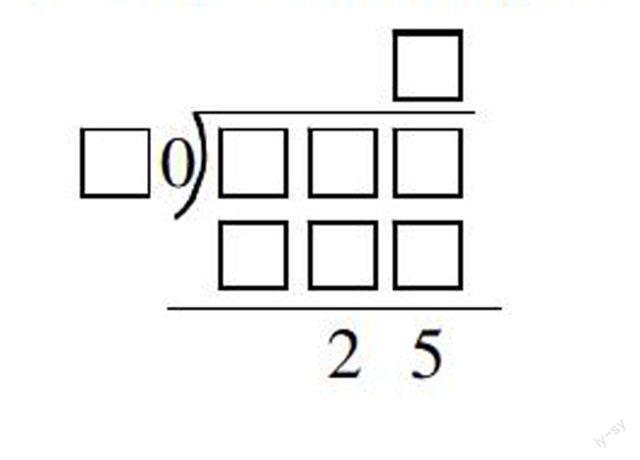
（4）拓展题. 用尽可能多的方法解决.

生12：我有6种方法， ， ， ， ，

， .

师：真聪明！一下子把结果都想出来了. 向同学说说你的想法.

生12：先确定除数，余数要比除数小，假如除数最小是30，可30 × 3 = 90，积只有两位数，所以除数最小是40，40 × 3 + 25 = 145. 然后分别依次确定除数是50，60，…，90.

【思考二】

“数与代数”位于《数学课程标准》指定的四大领域之首，在实际生活与生产中有着极为广泛的应用. 老师们普遍认为计算课枯燥乏味，学生往往是进行着机械的运算，第一次教学确实有这样的痕迹，课堂气氛略显冷淡；在第二次教学时，通过调整教学细节，这些现象几乎消失，彰显出计算教学的活力，体现出关注细节的价值. 具体体现在以下三方面：

1. 全面参与重点知识的感悟

用竖式笔算中商的定位是本课的重点，自然需要学生的全员参与. 人人参与的课堂是充满活力的课堂，活力来自三个方面. 一是学生都亲历了例1（92 ÷ 30）的尝试；二是两名学生代表性地展示了自己的尝试结果；三是组织四人小组、全体学生两个层面的讨论，对一正一误两种尝试结果进行思辨，在尝试、展示、思辨的过程中，学生领悟到商的定位的正确方法.

2. 充分经历难点知识的体验

新课程十分重视学生对知识、过程和方法的经历与体验. 例2（ ）三位数除以整十数“被除数前两位不够除时，要看前三位”是本课的教学难点，这个结论是否由学生自己领悟后得出，是难点是否突破的指标. 在学生尝试例2的基础上，再次尝试两道类似练习，使学生充分经历试商方法的体验，然后运用对比的数学思想方法，引导学生找出两类计算题的表面区别，接着，教师一句“为什么这六题的商都是一位数？”的提问，让同桌学生开展讨论，把学生的思维引到知识的核心，于是，学生透过现象看到了本质，水到渠成地得出了结论，学生的抽象、概括能力也由此得到提升.

3. 主动寻求应用知识的策略

《数学课程标准》要求：“面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻求解决问题的策略. ”落实这一要求，需要教师精心设计，提供机会. 经过微调后的练习题（3）和（4），紧扣目标，情景逼真，适度开放，是培养学生解决问题策略的有效练习，是进行思维训练的理想材料. 课堂上，我们清晰而欣喜地耳闻目睹学生的表现，他们思维活跃，策略得当，说理透彻，思考有序，把学习活动推向了高潮.

如果说，本课第一次尝试做到了大气，那么第二次尝试在大气之中达到了精细. 大气而精细的课堂，才是充满生机和活力的课堂！