二重积分的计算方法
2015-05-30蒋银山
蒋银山
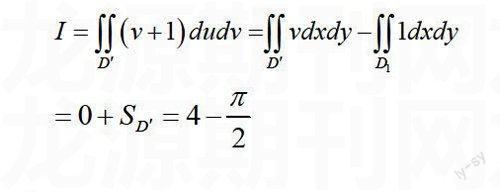


【摘要】二重积分的计算方法有⑴利用直角坐标计算二重积分,⑵利用极坐标计算二重积分,⑶利用积分区域的对称性与被积函数的奇偶性计算二重积分,⑷利用分块积分法计算二重积分,⑸利用坐标轴的平移计算二重积分。
【关键词】二重积分;直角坐标;极坐标;平移及奇偶性
二重积分的计算方法有⑴利用直角坐标计算二重积分,⑵利用极坐标计算二重积分,⑶利用积分区域的对称性与被积函数的奇偶性计算二重积分,⑷利用分块积分法计算二重积分,⑸利用坐标轴的平移计算二重积分。
计算二重积分有一定的步骤,我们大致分成4步。第一步:画出积分区域 的草图,判断积分域是否有对称性,被积函数是否有奇偶性;第二步:选择坐标系;第三步:选择积分次序;第四步:确定积分限并计算累次积分。
例题1.计算二重积分 其中积分区域 是由 与曲线 所围成。
方法一:利用直角坐标计算二重积分
解:积分区域
=
方法二:利用坐标轴的平移及奇偶性计算二重积分
解:设 作坐标轴的平移,在 平面上积分区域为
① 關于 对称,被积函数关于 是奇函数,
②
③
例题2.计算 其中积分区域 是由 所确定。
方法一:利用极坐标法计算二重积分
方法二:利用坐标轴的平移及极坐标计算二重积分
令 此时 ,则
方法三:利用坐标轴的平移及奇偶性计算二重积分
由于
利用奇偶性可得 而 ,则
方法四:利用积分区域的对称性计算二重积分
解:积分区域 关于 对称且为圆域故形心的坐标在圆心
其中 为积分区域 的形心的横坐标。
例题3:求计算二重积分 其中积分区域 是由 及曲线 所围成。
分析:若把 看成正方形的区域挖去半圆 ,则计算 上的积分自然选用极坐标变换,若只考虑区域 ,则自然考虑先 后 的积分次序化为累次积分,若注意 关于直线 对称,选择平移坐标变换则最为方便。
方法一:选择先 后 的积分次序,则
方法二:方块积分法及极坐标法
在极坐标下
方法二:利用坐标轴的平移计算二重积分
作平移变换则
参考文献:
[1]李正元,李永乐,袁荫棠:《 数学复习全书》,国家行政学院出版社,2013(2).
[2]武忠祥,《高等数学强化讲义》,西安交通大学出版社,2011(4).
