例谈数学方法在解决地理问题中的应用

臧丽芹

地理学是一门研究领域十分广泛的学科。在中学阶段，地理被归为文科，但由于其考察、运算等方面的要求使得其与数学学科的关系密切。利用数学方法解决地理问题，常能获得事半功倍的效果。常用于解决地理问题的数学方法有：作图法、借用数学定理法方程计算法、反证法等。

一、作图法

例1.当地球上今天与昨天的比例为1∶3时，求北京时间。

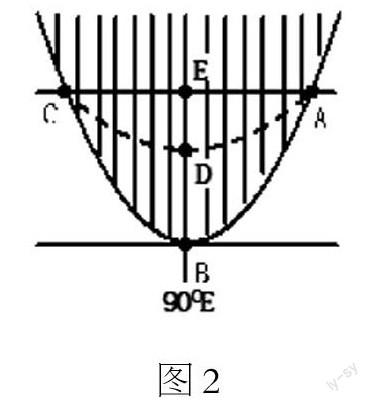
分析：对于类似的题目，作图求解更加简单直观。可以作以北极点为中心的俯视图，阴影部分表示昨天的范围，由于地球上两条日期分界线分别为180度经线所代表的国际日期变更线，以及地方时为零点的经线。据图可以判断下图中OB为180度经线，OA为地方时为零点的经线，且 OA为东经90度，则可以推出北京时间为今天的2点。在讲解的过程中还可以自由变换2天的比例，或者明确具体的日期来给学生做变式训练。

二、方程计算法

例2.读图，阴影表示黑夜，B点的正午太阳高度为42°， 求此时太阳直射点的地理坐标。

分析：本题太阳直射点的经度坐标一目了然即，太阳直射点的纬度坐标则需要使用方程法来计算求解。图中B点所在纬线即为与晨昏线相切的纬线，其纬度与太阳直射点的纬度互余。由于B点以南为极昼则太阳直射点位于南半球。

解：假设太阳直射点的纬度为X，则根据B点的正午太阳高度为42°可以列出方程：

90°-┃（90°-X）-X┃=42°       X=21°S

三、借用数学定理

例3.图同例2

问：A至C的最短路径为：（     ）

A、A-E-C   B、A-D-C     C、A-B-C

分析：有些同学往往直观的认为A至C的最短路径为A-E-C，其实不然。为回答这一问题我们还是先看一看高中立体几何中有关球体的一些知识：球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫小圆。当我们把地球视作一个球时，经线就是球面上从北极到南极的半个大圆，赤道是一个大圆，其余的纬线都是小圆。在球面上，两点间的最短距离就是经过这两点的大圆，也就是这两点间的一段劣弧的长度。我们把这个弧长叫做两点的球面距离。飞机、轮船都尽可能的以大圆弧为航行线。如果知道了这些立体几何知识，回答上面的问题，是不言而喻的，因为晨昏线就是地球上的一个大圆，所以应该选择路线A-B-C。

四、反证法

例4.如图所示，曲线为等压线，直线为锋线，阴影为降水区，据此回答下列问题：

（1）O1为                     （低压、高压）中心。

（2）甲地位于                    （南、北）半球。

（3）判断甲地锋面的性质：                            。

（4）判断a、b两处的风向：                              。

（5）判断a、b两处气团的冷暖性质：                            。

分析：本题属于对锋面气旋的考察，O1为低压中心，而解题的关键在于需要先判断甲地位于南半球还是北半球。我们可以作出假设：先假定其位于南半球，画出a、b两点的风向，a为偏东风，b为偏北风，而b来自于南半球较低纬度，可看作暖气团，则可判断该锋面属于暖锋。而暖锋的主要降水区域应位于锋前即a侧，明显与图示不符，因此“甲地位于南半球”的假设不成立，所以甲地应位于北半球。

作者单位   南京市第二十九中学

编辑   薛小琴