几何入门训练十法

徐登高

摘 要：如何抓好平面几何的入门教学，是教好平面几何的关键，初中学生年龄小，逻辑思维能力的发展不能完善，容易对平面几何的学习产生畏惧感。如果开始时学不好，会给后续的学习带来困难，这就会影响整个平面几何的学习。

关键词：几何；入门教学

几何是研究图形及其性质的一门学科，初中学生在由数到形的过渡阶段，如起步不好会导致对数学一科丧失信心。为此，我采取了以下方法训练几何入门：

一、联系实际，激发兴趣

在教学过程中，采取举例子、看实物、打比方、画草图、做实验等方法，使学生认识到几何学在我们的生活中，并不难学；另一方面使学生知道观察并不可靠，要作出判断，必须进行严密推证。如用纸折叠找中点，找角平分线，拼凑三角形内角和，过A、B两点用不同颜色的粉笔画直线，观察“两点确定一条直线”。按如图所示的位置关系量等长线段AB和CD的长，使学生发现视线欺骗了我们等实践活动，让学生的眼、手、口、耳、脑积极参与整个教学过程激发学生几何学的兴趣。

二、变机械记忆为灵活填充

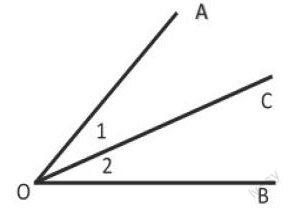
针对入门阶段，名称、术语、定理、公理较多的特点，采取按知识的正逆、是非、易混、易错处，编出填空、选择、改错、默写等作业，让学生在实践中准确、灵活地掌握双基。例如：按角平分线可编成几类题：① 是角平分线；②OC平分∠AOB，则∠ =∠ ；③OC平分∠AOB，则∠ =1/2∠ ，∠ =2∠ ；④如图，已知∠1=∠2，则 线 是 的平分线。

三、亲自动手，发现“新大陆”

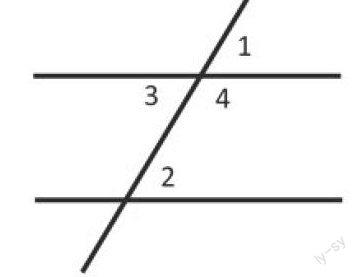
对于任何证明途经和新定理的出现，教师不先和盘托出，采取引导学生利用旧知识自己去猜想、去发现“新大陆”的方法；让学生在历经苦索中，学到探讨问题的方法，加深对知识的理解。如讲平行判定定理时，先让学生通过作两条直线与第三条直线相交，并使同位角相等，然后观察是否平行（按定义想）；再提出如果内错角相等，同旁内角互补，则两条直线是否平行的疑问。让学生通过图形观察∠3和∠1，∠4和∠1的关系，明白由∠1=∠2可以推出∠3=∠2，∠4+∠2=180°，从而得到判定定理二、三。

四、分散重点，单行训练

针对初学几何阶段的学生存在分不出已知、求证，由题意画不出图形的困难，而导致证明无法起步的实际，对学生进行以下两项单行训练：

帮助学生区分，命题中的条件和结论。从以下三方面入手：①用“如果……那么……”等关联词辨认；②加关联词辨认，例如：“对顶角相等”变为“如果两个角是对顶角，那么这两个角相等”；③用肯定和否定区别，例如：“等腰三角形底角的平分线相等”，肯定的对象是等腰三角形底角的平分线，肯定的结果是相等，然后告诉学生这个“对象”就是题设，其结果是结论，并出一组题目进行此项训练。

五、抓好示范，做好铺垫

一是教师从开始就要求学生回答问题，进行计算有理有据；二是利用书上的填充题训练说理的条理性，证明的严密性及书写的规范性训练，采用先照着书本做填空练习，再背着书独立证明已做过的填充题。最后，对着书自查（条理性、严密性及书写格式），为独立分析、证题打好基础。

六、加强推理，注重分析

随着命题的加深与推理的复杂化，要逐步加强分析与综合相结合的逻辑思维训练，把教与学的重点放在分析问题上。针对初学几何的学生易犯罗列一大堆与求证无关的条件或缺少条件也能得出结论的毛病，我从一开始就使用推出式证明方法。强调用箭头“”画出分析图，既要“证××，只要证××，再证××”等。二是把证明的整个思维步骤编成口诀，要求学生按照步骤去想问题，即：一边读（审题），一边批（把已知、求证搬到图形上），一边想（有关的定理、公理），一边推（条件的发散），再从结论往前追（画分析图），到写回去不累赘（用推出式写出证明）。

七、加强总结，掌握规律

一是随着内容的增多，不断启发学生沟通证明的各种渠道。如要证明两个角相等：①证是角平分线，②用平行线性质证，③用等量代换，④同一三角形中证角所对的边也相等，⑤证三角形全等……

二是举典型例子探求同类题目的解题规律。如：初学造辅助线学生感到棘手，我利用下例讲明辅助线一般造平行线或连接两点，要以造后得出全等三角形或有等角出现为依据去思索，使辅助线成为分析基础上的产物，例如：

已知：在△ABC中，AB=AC，DE交AB于D，交BC于F，交AC的延长线于E，DF=EF，求證：BD=CE。

八、改革作业，提高效率

由于学生的教学基础和理解能力的不同，导致部分同学抄袭作业，为了堵住这个缺口，并把教师从繁重的批改作业中解放出来，采取如下方法处理作业：练习题当堂独立做，马上对结果，使之及时反馈，课本上的难题采用课堂讨论，大家一起想，再按各人讲的方法验收，使差生在优生的辅导下完成难题，中档题采用当天布置，第二天独立作业，使差生有回旋的余地（课外思考），达到掌握程度，教师只批改验收作业，既可减轻负担，又可得到真实的反馈信息。

九、针对弱点，定向训练

为了避免简单重复，对学生作业中出现的错误，除分析原因外，有针对的出一组定向训练题，以便及时消除隐患，促使差生不差，避免两极分化。

十、抓章节复习，严格把关

复习要有明确标准，查缺补漏，开拓思路，培养能力的原则，一般做四套题目：①按知识结构复习后，做一份双基训练题（侧重查漏）；②按题型归类后，考一份类型题（侧重开拓思路）；③进行综合复习，做一份综合试题（侧重査能力）；④按大纲要求出一份有梯度的题目作为本章的过关题。对单元过关优胜者予以鼓励，并帮助差生找原因，树信心，进行补习验收，把提高整个数学成绩的任务，落实到每一个章节的教学中去。

（作者单位：庐山中学）