源于定义的三视图问题求解对策
2015-05-30韩天禧
韩天禧


关于三视图的定义,教材是这样给出的,“光线依次从几何体的前面向后面、左面向右面、上面向下面的正投影,分别叫做几何体的正视图、侧视图、俯视图,几何体的正视图、侧视图和俯视图,统称为几何体的三视图”。三视图的定义图文并茂、简洁明快,但缺少数学属性,好记忆难应用。要深度理解三视图的定义,必须从图形中挖掘特征量,从投影的物理方法与过程中提炼数学本质,来丰富三视图的定义的内涵。
一、三视图的定义评析
1.三正要义
三视图是在空间设置互相垂直的三个正立面(正面、水平面、侧立面)作为投影面,是在物体正放、视线正对着物体的前提下,向这三个面上进行投影得到的三个视图。其中,互相垂直的三个正立面是三视图的空间载体,三个方位的正投影是成图的物理方法与过程,三个正立面上的三个空间正投影展到同一平面上,是平面三视图的最终归宿。毫不夸大地说,“三正”是作三视图的操作起点与动作指令。
2.点是本源
线、面、体的根在于点,作几何体各顶点的投影点,各顶点的投影如同若干钢针正钉在投影面上,在投影面上由点生线(眼见为实,不见为虚),由线生面,得到对应的三个视图。
3.三等关系
三个视图的长、宽、高分别指几何体所占空间的左右、前后、上下的最大距离。由每两个视图都有相同的可视量,得正视图与俯视图的长、正视图与侧视图的高、侧视图与俯视图的宽都相等,即“长对正、高平齐、宽相等”,这个三等关系体现了三个不同方位的视图的必然联系。
4.三位关系
投影后要把在空间的三个视图展开摊平到同一个平面内,即正视图不动,侧视图逆转90。放在正视图右侧,俯视图下旋90。放在正视图下方,由此得出的“三位关系”是自然形成的,而不是人为摆放的。
5.数位关系
“三等”与“三位”关系是不可分割的整体,数中有位,位不离数,相辅相成地呈现出三个视图之间的联系。
6.逆向回转
三视图的形成与还原是互逆的,投影与平移、平展与翻折相互对应。由三视图还原几何体时,先将三个视图翻折到空间互相垂直的三个正立面上,然后将三视图中的局部线段,凭借空间想象力,依次向前后、左右、上下平移,使得“长对正、高平齐、宽相等”,还原出三视图对应的空间几何体。
二、三视图问题的求解对策
从以上定义评析中发现,空间几何体的三视图与长方体的关系是休戚相关的,我们不妨就请长方体这个“瓮”,来捉三视图这只“鳖”。
1.请“君”入“瓮”
在作几何体的三视图时,若将几何体镶嵌在长方体中,不仅三个正立面是现实直观的,再无需凭空想象,而且作投影时前后、上下、左右处处都有可供参考的线面垂直与线线平行关系,这个长方体就是最美正投影的关系网,所以只要把几何体请到长方体中,作空间几何体的三视图就是水到渠成、顺理成章的事了。
例1将正三棱柱截去三个角(如图1,A、B、C分别是△GHI三边的中点),得图2所示的几何体,则该几何体按图2所示方向的侧视图是()。
解析:将图2所示的几何体ABC-EFD放人图4所示的长方体中,作几何体各顶点在侧立面上的正投影,即B与C两点的投影为点N,点A的投影为点G,点E的投影为点D,点F的投影为点M,依次连接各投影点,得该几何体从左到右的投影为直角梯形M DDGN,再将该投影沿线段DG按逆时针方向旋转90。得侧视图。应选A。
点评:其实就是把空间几何体内接在长方体之中,为减少作图量,尽可能地把几何体中的点、线、面放到长方体各面上。
例2某几何体的一条棱长为√7,在该几何体的正视图中,这条棱的投影是长为√6的线段,在该儿何体的侧视图与俯视图中,这条棱的投影分别是长为“和b的线段,则a+b的最大值为()。
A.2√2
B3.2√3
C.4
D.2√5
解析:不妨构造一个体对角线长为√7的长方体,如图5所示,使D1B一√7,D1C=√6,a=BC1,b=BD。时,等号成立。
点评:把几何体的这条棱视为长方体的一条体对角线,它对应的三个视图就是这个长方体的三个面对角线,在找体对角线与面对角线间的关系时,还需要设出长方体的长、宽、高作为媒介。对于本题,若脱离具体的长方体模型是难以入手的。
2.“瓮”中捉“鳖”
由三视图还原几何体,它与作几何体的三视图是一个互逆过程,其思路是:以三视图的长、宽、高作一个长方体,将正视图、侧视图和俯视图依次放到长方体的后侧面、右侧面和下底面上,把三个视图的部分线段,依次向前、向左、向上平移,使得“长对正、高平齐、宽相等”,就能快捷地还原出几何体。
例3一个棱锥的三视图如图6所示,则该棱锥的全面积为()。
A.48+12√2 I3.48+24√2
C.36+12√2 D.36+24
解析:如图7,在长方体的三个面上作出该几何体的正视图、俯视图、侧视图,分别为△NAD、△MCD、△ABC,线段QM在侧立面上的投影为M点,线段PN在正对面上的投影为N点,记QM、PN的交点()1为棱锥的顶点,将CD平移到BA处使俯视图与侧视图的宽相等(重合),AD平移到BC处使正视图与俯视图的长对正,由此得到三视图对应的空间几何体为三棱锥O1-ABC。经反向验证,该几何体满足要求。
在图7中,O为AC的中点,O1O=4,AB=BC=6,AC一6√2,三棱锥O1-ABC的两侧面△O1AB与△O1BC是全等的等腰三角形,由此得三棱锥01-ABC的全面积为:S=S△O1AB+S△O1BC+S△O1AC+S△ABC =48+12√2。
点评:只要心中有图,不一定非要作出一个具体的长方体,可将三个视图假想在长方体的三个面上,经过翻折后,做到三个重合,凭着空间想象能力也能还原出空间几何体。
例4已知正四面体(所有棱长都相等的三棱锥)的俯视图如图8所示,其中四边形是边长为2的正方形,求这个正四面体的正视图的面积。
解析:作底面为正方形的长方体,如图9所示,取底面正方形各边的中点A、N、B、M,则正方形ANBM为正四面体的俯视图。
由于AB=MN,只有将俯视图的可视线段AB沿竖直方向平移到长方体上底面上的PQ位置时,才能使正四面体的两条棱PQ与MN的长相等,由此得到正四面体P-MNQ,它的正视图为△CDM。
由AN =2,得正四面体的棱长为PQ=2√2。
在Rt△QAN中,AQ= =2。
正四面体的正视图△CDM的面积为S△CDM=
点评:由此看出,在长方体中还原空间几何体,可轻松逾越命题者预设的考查较强空间想象力的难度,如对于本题,使抽象的几何体的特征与俯视图,不仅直观形象地在长方体中相互照应与调整,而且当几何体确定后,它的正视图也就显而易见了。尤其是利用长方体作工具,可直接把三视图中的数量关系转移到对应的空间几何体上,利用直角三角形求解未知量时也简单。
G.波利亚在《怎样解题》中说:“画一个假设图形,假设它的各个部分都满足题目条件,也许是迈出解题的重要一步”。照此办理,在解决三视图问题时,将几何体镶嵌在长方体中作三视图,或用它把三视图统一在长方体中还原几何体,用这种请“君”入“瓮”与“瓮”中捉“鳖”的思路去解决问题,能化抽象为形象,方法简单、快捷又容易掌握。
跟踪训练
1.(2013年高考湖南理)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()。
A.1
B.
c.
D.
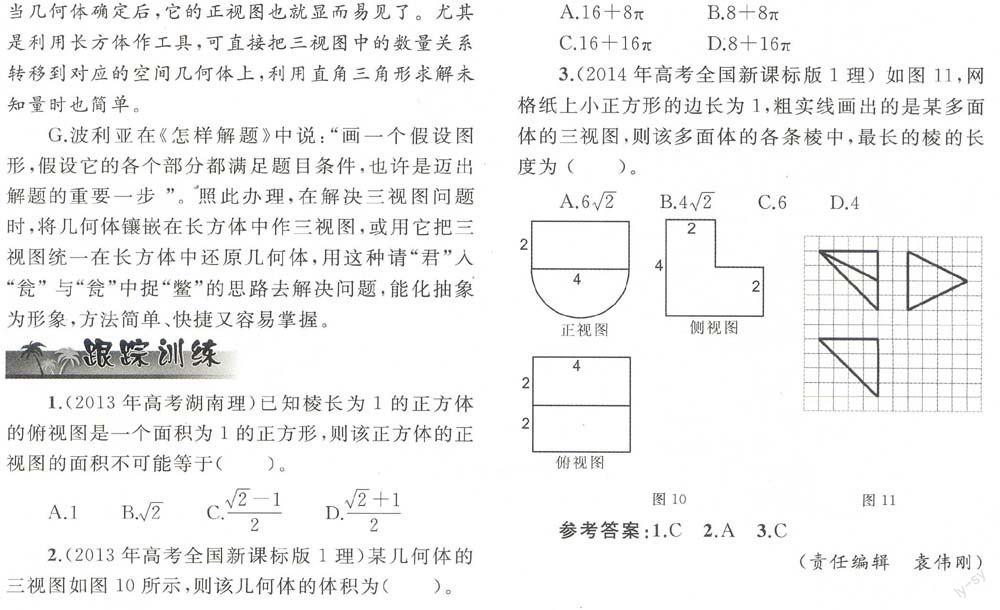
2.(2013年高考全国新课标版1理)某几何体的三视图如图10所示,则该几何体的体积为()。
A.l6+8π
B.8+8π
C.16十l6π
D:8+16π
3.(2014年高考全国新课标版1理)如图11,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()。
A.6√2
B.4√2 C.6 D.4参考答案:1.C 2.A 3.C
